第八章LDPC码 8.1研究LDPC码的原因 BCH 码 码 循环码 RS码 线性 信 分 系统卷 码 奇偶 积码 Tu胸 LDPC 非循环 校验 码 码 非系统 非线 码 卷积码 性码 汉明 码 Mackay等人的再发 现 可以看到,信道编码的发展可以简单的归纳为分组码→卷积码→分组 码这样一个过程(在这里按其结构将Tubo码也归入卷积码的范畴)。 其中Tubo码的出现以及迭代译码的思想引入使得信道编解码产生 了前所未有的飞跃,但Tubo码之后卷积码却没有更大的发展,究其 原因就是其没有完备的理论基础,使得人们不能给出其性能上严密的 数学解释。于是在那之后可以说是一种退化或者是返朴归真,Mackay 等人再次发掘了Gallager于1962年提出的一种具有稀疏校验矩阵的 分组纠错码,即LDPC码。 LDC码和传统的分组码最大的区别在于它们的译码。分组码通常是 用最大似然译码,因此,码长一般较短,并用代数方法设计使得复杂 度较低。而LDPC码是迭代译码,校验矩阵用Tanner图表示,码长更 长、围绕着校验矩阵H的特性进行设计是核心。 LDPC码自身的矩阵结构引入了交织特性,而且其采用迭代译码的
第八章 LDPC 码 8.1 研究 LDPC 码的原因 分 组 码 卷 积 码 线性 码 非线 性码 非系统 卷积码 系统卷 积码 循环码 非循环 码 汉明 码 奇偶 校验 码 RS码 BCH 码 Turbo 码 LDPC 码 信 道 编 码 Mackay等人的再发 现 可以看到,信道编码的发展可以简单的归纳为分组码卷积码分组 码这样一个过程(在这里按其结构将 Turbo 码也归入卷积码的范畴)。 其中 Turbo 码的出现以及迭代译码的思想引入使得信道编解码产生 了前所未有的飞跃,但 Turbo 码之后卷积码却没有更大的发展,究其 原因就是其没有完备的理论基础,使得人们不能给出其性能上严密的 数学解释。于是在那之后可以说是一种退化或者是返朴归真,Mackay 等人再次发掘了 Gallager 于 1962 年提出的一种具有稀疏校验矩阵的 分组纠错码,即 LDPC 码。 LDPC 码和传统的分组码最大的区别在于它们的译码。分组码通常是 用最大似然译码,因此,码长一般较短,并用代数方法设计使得复杂 度较低。而 LDPC 码是迭代译码,校验矩阵用 Tanner 图表示,码长更 长、围绕着校验矩阵 H 的特性进行设计是核心。 LDPC 码自身的矩阵结构引入了交织特性,而且其采用迭代译码的

方法,使其性能比以往的线性分组码有很大程度的提高。由于其基本 原理是基于最原始的线性分组码,因此它有强大的数学工具作为其理 论依据,几乎融图论、组合数学、概率论、矩阵论、代数、几何、代 数数论、黎曼几何于一炉。在通信的其它领域,我们很难再找到某个 方向可以有如此深厚的理论基础与之媲美。 但理论上的完备性并不能使其直接应用于实际,因此从码字构造 的方向来说,如何将LDPC码应用于实际工作才是值得深入研究的。 为了保证其实现性,性能上就要有所妥协。 在编码方面,以准循环LDCP码,即QC-LDPC码为例,为了降低 硬件上的存储空间以及易于编码,就要以牺牲LDPC码先天的优势一 一交织特性为代价,这样便做出了性能与实现上的折中。但这种折中 是有意义的,为LDPC码的实际应用开辟了道路。而且,通过某些方 法,可以使设计出的码字在易于存储实现的同时,还能保证一定的性 能。 在译码方面,种种方法都可以归结为和积算法(SPA)的变形,都 是在其基础上做出改进,从而保证译码性能前提下使译码器尽可能的 简单。相对于Tubo码,LDPC码的解码迭代次数还是过高,这样在 实际应用中的竞争力便大打折扣。于是,怎样在保证性能的前提下降 低译码时间是现在译码研究的主要工作。 8.2LDPC码简介 1996年Mackay、Spielman和Wiberg几乎同时发现:Gallager
方法,使其性能比以往的线性分组码有很大程度的提高。由于其基本 原理是基于最原始的线性分组码,因此它有强大的数学工具作为其理 论依据,几乎融图论、组合数学、概率论、矩阵论、代数、几何、代 数数论、黎曼几何于一炉。在通信的其它领域,我们很难再找到某个 方向可以有如此深厚的理论基础与之媲美。 但理论上的完备性并不能使其直接应用于实际,因此从码字构造 的方向来说,如何将 LDPC 码应用于实际工作才是值得深入研究的。 为了保证其实现性,性能上就要有所妥协。 在编码方面,以准循环 LDCP 码,即 QC-LDPC 码为例,为了降低 硬件上的存储空间以及易于编码,就要以牺牲 LDPC 码先天的优势— —交织特性为代价,这样便做出了性能与实现上的折中。但这种折中 是有意义的,为 LDPC 码的实际应用开辟了道路。而且,通过某些方 法,可以使设计出的码字在易于存储实现的同时,还能保证一定的性 能。 在译码方面,种种方法都可以归结为和积算法(SPA)的变形,都 是在其基础上做出改进,从而保证译码性能前提下使译码器尽可能的 简单。相对于 Turbo 码,LDPC 码的解码迭代次数还是过高,这样在 实际应用中的竞争力便大打折扣。于是,怎样在保证性能的前提下降 低译码时间是现在译码研究的主要工作。 8.2 LDPC 码简介 1996 年 Mackay、Spielman 和 Wiberg 几乎同时发现:Gallager

早在1962年提出的低密度校验码(简称LDPc码,也称Gallager码) 也是一个好码,具有更低的线性译码复杂度。Gallager提出LDPc码 后一直没有得到编码界的重视,只有1981年Tanner从图论的角度研 究过LDPC码。 自Mackay等“再发现”LDPC码后,人们的进一步研究表明:给 予非规则双向图的LDPC长码的性能可以优于Tubo码,而且这样的 码的性能可以非常接近Shannon限。一个原因在于LDPC码具有良好 的距离特性、较小的译码错误概率和较低的译码复杂度,且码长大于 200时不存在错误平台,码率容易调整,实验结果中几乎均为可检测 错误,所以LDPC码无论在理论上还是在实际上都具有极其重要的价 值。LDPc码的重新发现是继Tubo码后在纠错码领域又一重大进展。 (1)编码方面的简介 无论Gallager还是Mackay都是用随机的方法构造LDPC码,用 随机法构造的LDPC码的码字参数选释灵活,但对于高码率、中短长 度的DPC码用随机法进行构造,要避免短循环是困难的,其没有一 定的码结构,编码复杂度高,于是人们考虑用代数法构造LDPC码。 LDPC码代数构造可采用几何方法、图论方法、实验设计方法、 置换方法来设计。不同的构造方法都是为了实现以下几个目的:增大 图中最小循环长度,即Gith值。优化非规则码的节点分布,减小编 码复杂度,构造的LDPC码要有好的码性能。 M.G.Luby等指出,非规则H矩阵构造的码字性能优于相应的规 则H矩阵构造的码字。在寻找好的码结构方面,Mackay等提出:能
早在 1962 年提出的低密度校验码(简称 LDPC 码,也称 Gallager 码) 也是一个好码,具有更低的线性译码复杂度。Gallager 提出 LDPC 码 后一直没有得到编码界的重视,只有 1981 年 Tanner 从图论的角度研 究过 LDPC 码。 自 Mackay 等“再发现”LDPC 码后,人们的进一步研究表明:给 予非规则双向图的 LDPC 长码的性能可以优于 Turbo 码,而且这样的 码的性能可以非常接近 Shannon 限。一个原因在于 LDPC 码具有良好 的距离特性、较小的译码错误概率和较低的译码复杂度,且码长大于 200 时不存在错误平台,码率容易调整,实验结果中几乎均为可检测 错误,所以 LDPC 码无论在理论上还是在实际上都具有极其重要的价 值。LDPC码的重新发现是继Turbo码后在纠错码领域又一重大进展。 (1)编码方面的简介 无论 Gallager 还是 Mackay 都是用随机的方法构造 LDPC 码,用 随机法构造的 LDPC 码的码字参数选择灵活,但对于高码率、中短长 度的 LDPC 码用随机法进行构造,要避免短循环是困难的,其没有一 定的码结构,编码复杂度高,于是人们考虑用代数法构造 LDPC 码。 LDPC 码代数构造可采用几何方法、图论方法、实验设计方法、 置换方法来设计。不同的构造方法都是为了实现以下几个目的:增大 图中最小循环长度,即 Girth 值。优化非规则码的节点分布,减小编 码复杂度,构造的 LDPC 码要有好的码性能。 M.G.Luby 等指出,非规则 H 矩阵构造的码字性能优于相应的规 则 H 矩阵构造的码字。在寻找好的码结构方面,Mackay 等提出:能

快速编码的LDPC矩阵通常具有下三角形结构。 TJ.Richardson探讨了如何构造编码矩阵,使编码时间与码块长 度实际上符合线性关系(线形时间编码),而非通常认为的平方关系。 Y.Kou和s.Lin等探讨了基于有限几何学的LDPc码结构。S.Lin研 究团队的B.Ammar等提出用均衡不完全区组设计方法(BlBD)构造 好的LDPC码。 (2)译码方面的简介 Gallager曾给出两种LDPC码的迭代译码算法:硬判决和软判决 算法。后者虽有好的性能,但太复杂,消息传递算法可以认为是二者 的折衷。消息传递算法(MP,Message Passing)有时也称置信传播 (BP,Belief Propagation)算法。在MP译码算法中,节点到节点的 消息是通过Tanner图传递的。 译码算法的改进和优化离不开译码性能的分析。在译码性能分析 的研究方面,TJ.Richardson等开发了一种在码块无限长假设条件下, 跟踪LDPc码Tanner图中消息概率的技术,称为“密度进化”算法的 数值程序,来近似估计噪声门限(在该门限以下可望成功地采用BP 算法),提出了一种通用方法来确定任何二元输入无记忆信道中采用 MP译码的LDPC码的性能。特别对于BP译码算法,该方法可提供任 何所需精度的性能估计。 s.Y.Chung等将消息离散化,通过计算机迭代搜索寻找最优的节 点次数分布,特别适合于非规则码的分析,在二进制输入AWGN信 道下,设计码率1/2、码张10'的非规则LDP℃码在错误概率106时离
快速编码的 LDPC 矩阵通常具有下三角形结构。 T.J.Richardson 探讨了如何构造编码矩阵,使编码时间与码块长 度实际上符合线性关系(线形时间编码),而非通常认为的平方关系。 Y.Kou 和 S.Lin 等探讨了基于有限几何学的 LDPC 码结构。S.Lin 研 究团队的 B.Ammar 等提出用均衡不完全区组设计方法(BIBD)构造 好的 LDPC 码。 (2)译码方面的简介 Gallager 曾给出两种 LDPC 码的迭代译码算法:硬判决和软判决 算法。后者虽有好的性能,但太复杂,消息传递算法可以认为是二者 的折衷。消息传递算法(MP,Message Passing)有时也称置信传播 (BP,Belief Propagation)算法。在 MP 译码算法中,节点到节点的 消息是通过 Tanner 图传递的。 译码算法的改进和优化离不开译码性能的分析。在译码性能分析 的研究方面, T.J.Richardson 等开发了一种在码块无限长假设条件下, 跟踪 LDPC 码 Tanner 图中消息概率的技术,称为“密度进化”算法的 数值程序,来近似估计噪声门限(在该门限以下可望成功地采用 BP 算法),提出了一种通用方法来确定任何二元输入无记忆信道中采用 MP 译码的 LDPC 码的性能。特别对于 BP 译码算法,该方法可提供任 何所需精度的性能估计。 S.Y.Chung 等将消息离散化,通过计算机迭代搜索寻找最优的节 点次数分布,特别适合于非规则码的分析,在二进制输入 AWGN 信 道下,设计码率 1/2、码长 107的非规则 LDPC 码在错误概率 10-6时离

Shannon限仅0.0045dB。这是迄今为止报道出的性能最接近Shannon 限的信道编码。 8.3LDPC码的基本概念 LDPC码是用一个稀疏的非系统的校验矩阵H定义的线性码。 行重:H矩阵每行中“1”的个数,其值远远小于H矩阵的列数。 列重:H矩阵每列中“1”的个数。 LDPc码可以按照H矩阵分为规则(regular)和非规则(irregular) 两种。规则LDPC码中,各行的行重是一致的,各列的列重也是一致 的,而行重或者列重不一致就称为非规则LDPC码。 下面给出规则LDPC码的定义: 一个(n,j,k)的规则DPC码由它的校验矩阵H定义,校验矩阵 有n列,m行,列重,行重k,钟m=n·j/k,jk,jK<m,k<n。 LDPC码的H矩阵一般都是用非系统形式给出的。例如我们生成一 个6,2,4)的校验矩阵: [110110 0 H=1 1011 011101 如例所示的规则H矩阵行重为4,列重为2。 同一般的线性分组码,H矩阵的码率可以如下计算: R=n-m/n=k-j/k;则图中的矩阵可以用来实现码率1/2的编码。 对于一个非正则(irregular)LDPc码,我们常用度分布(degree distribution)来描述它。H中,列重为i的占比v:和行重为j的占比
Shannon 限仅 0.0045dB。这是迄今为止报道出的性能最接近 Shannon 限的信道编码。 8.3 LDPC 码的基本概念 LDPC 码是用一个稀疏的非系统的校验矩阵 H 定义的线性码。 行重:H 矩阵每行中“1”的个数,其值远远小于 H 矩阵的列数。 列重:H 矩阵每列中“1”的个数。 LDPC 码可以按照 H 矩阵分为规则(regular)和非规则(irregular) 两种。规则 LDPC 码中,各行的行重是一致的,各列的列重也是一致 的,而行重或者列重不一致就称为非规则 LDPC 码。 下面给出规则 LDPC 码的定义: 一个(n, j, k)的规则 LDPC 码由它的校验矩阵 H 定义,校验矩阵 有 n 列,m 行,列重 j,行重 k,其中 m njk = ⋅ / ,j<k,j<<m,k<<n。 LDPC 码的 H 矩阵一般都是用非系统形式给出的。例如我们生成一 个(6,2,4)的校验矩阵: = 0 1 1 1 0 1 1 0 1 0 1 1 1 1 0 1 1 0 H 如例所示的规则 H 矩阵行重为 4,列重为 2。 同一般的线性分组码,H 矩阵的码率可以如下计算: R=(n-m)/n=(k-j)/k;则图中的矩阵可以用来实现码率 1/2 的编码。 对于一个非正则(irregular)LDPC 码,我们常用度分布(degree distribution)来描述它。H 中,列重为 i 的占比 vi和行重为 j 的占比

h,则v=[2]和h=[h,h2]就是该码字的度分布。 例如: 110100 H=111001 011010 该码字的度分布v1=1/2、v2=1/3、3=1/6,h3=2/3、h4=1/3 ②mΣ4 其码率可表示为: 1* +2*1 ∑w-2 +3*1 5 1 r=1- 3 6=1- ∑jh 2 3* 10 2 3 3 3 LDPC码的校验矩阵的行对应着校验方程(校验节点),列对应 着传输的比特(比特节点),它们之间的关系可以用Tanner图来表 示,图的左边有n个节点,每个节点表示码字的信息位,称为比特节 点,=1,2,,n,对应于校验矩阵的各列,比特节点也称为信息节 点或变量节点;右边有m个节点,每个节点表示码字的一个校验集, 称为校验节点{,=1,2,,m,代表校验方程,对应于校验节点的各 行;与校验矩阵中“1”元素相对应的左右两节点之间存在连接边。 我们将这条边两端的节点称为相邻节点,每个节点相连的边数成为该 节点的度(Degree),每个比特节点与j个校验节点相连,称为该比
hj,则 v=[v1, v2,..]和 h=[h1,h2,…]就是该码字的度分布。 例如: 110100 111001 011010 H = 该码字的度分布 v1=1/2、v2=1/3、v3=1/6,h3=2/3、h4=1/3 i j i j n iv m jh ⋅= ⋅ ∑ ∑ 其码率可表示为: 111 5 1* 2* 3* 236 3 1 11 1 2 1 10 2 3* 4* 33 3 i i j j i v r j h ⋅ + + =− =− =− = ⋅ + ∑ ∑ LDPC 码的校验矩阵的行对应着校验方程(校验节点),列对应 着传输的比特(比特节点),它们之间的关系可以用 Tanner 图来表 示,图的左边有 n 个节点,每个节点表示码字的信息位,称为比特节 点{xj, j=1, 2, …, n},对应于校验矩阵的各列,比特节点也称为信息节 点或变量节点;右边有 m 个节点,每个节点表示码字的一个校验集, 称为校验节点{ri, i=1, 2, …, m},代表校验方程,对应于校验节点的各 行;与校验矩阵中“1”元素相对应的左右两节点之间存在连接边。 我们将这条边两端的节点称为相邻节点,每个节点相连的边数成为该 节点的度(Degree),每个比特节点与 j 个校验节点相连,称为该比
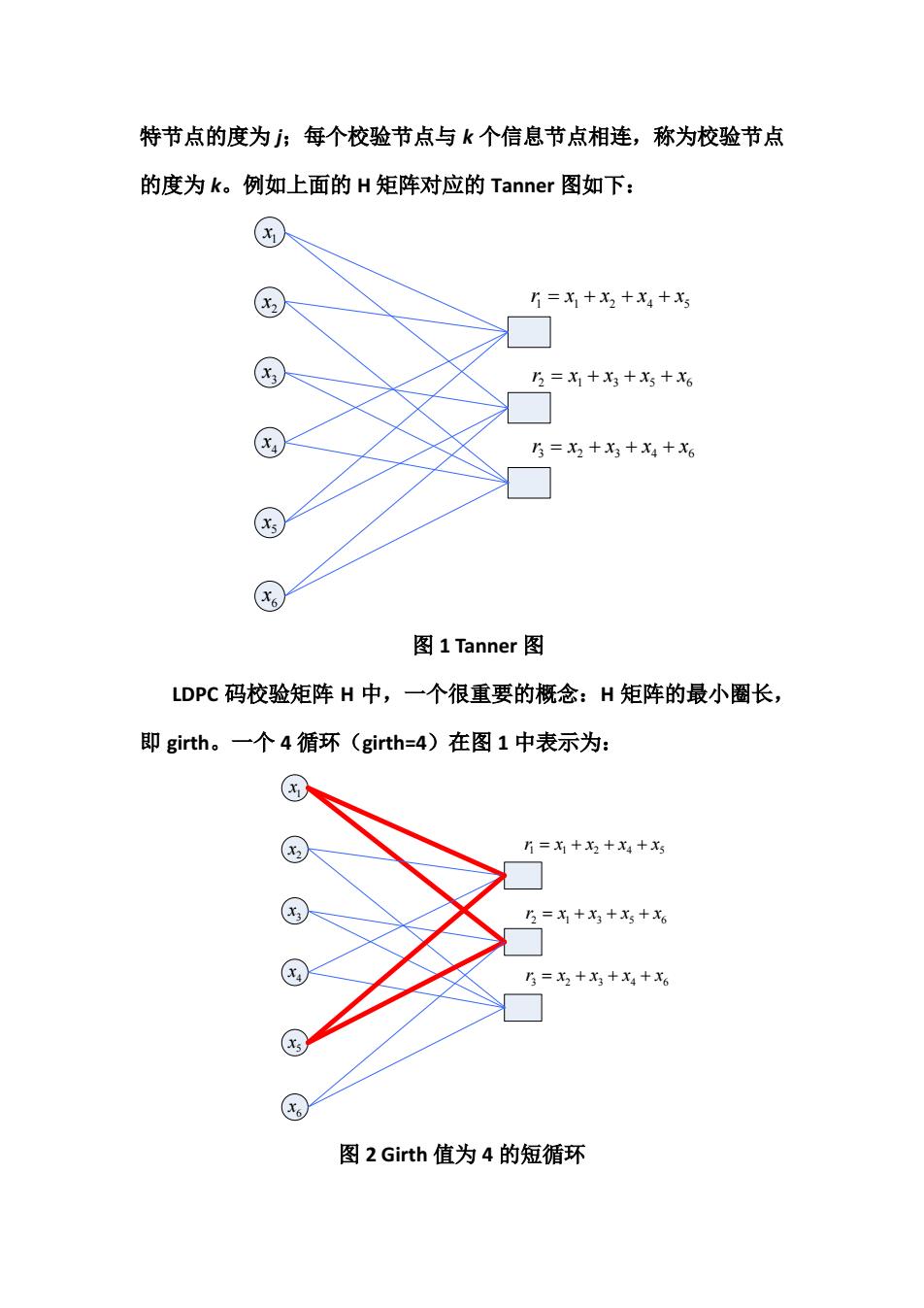
特节点的度为;每个校验节点与k个信息节点相连,称为校验节点 的度为k。例如上面的H矩阵对应的Tanner图如下: 2 5=x1+x2+X4+x 3 5=x1+x3+x+X6 乃=X2+X3+X4+X6 X5 6 图1 Tanner图 LDPC码校验矩阵H中,一个很重要的概念:H矩阵的最小圈长, 即girth.。一个4循环(girth=4)在图1中表示为: 片=x1+X2+x4+x 3=X1+X3+X+x6 3=X3+X3+x4+X6 图2 Girth值为4的短循环
特节点的度为 j;每个校验节点与 k 个信息节点相连,称为校验节点 的度为 k。例如上面的 H 矩阵对应的 Tanner 图如下: 1 x 2 x 3 x 4 x 5 x 6 x 11245 rxxxx =+++ 2 1356 r xxxx =+++ 3 2346 rxxxx =+++ 图 1 Tanner 图 LDPC 码校验矩阵 H 中,一个很重要的概念:H 矩阵的最小圈长, 即 girth。一个 4 循环(girth=4)在图 1 中表示为: 1 x 2 x 3 x 4 x 5 x 6 x 11245 rxxxx =+++ 2 1356 r xxxx =+++ 3 2346 rxxxx =+++ 图 2 Girth 值为 4 的短循环

对应于H矩阵,此4循环可以表达为: 9 H=1 011101 同理,对于6循环我们有: 上式所示的矩阵H1表示校验矩阵H中的一个子矩阵。 短循环对于矩阵性能的影响:在LDPC码的译码算法中,我们都 假设传递的消息满足彼此独立的假设。当H矩阵中存在长度为2L的 环路时,则这些消息只在前L轮迭代过程中满足独立性假设(注意: 解码的迭代过程包括一次比特节点更新和一次校验节点更新)。因此 短循环的存在会影响LDPC码的解码性能。 另外简单的解释:例如在图2所示的H矩阵中,存在一个4循环 于是这个4循环对应的校验方程为: T=x1+X2+X4+X5 =X1+X3+X5+X6 由于4循环的存在,我们可以看到,上面两个校验方程含有共同 的比特节点x1与x5,直观地说,如果这两个校验方程均出错,则我
对应于 H 矩阵,此 4 循环可以表达为: 101 0 010 1 011101 = 1 1 H 1 1 同理,对于 6 循环我们有: 101 110 011 = H1 上式所示的矩阵 H1表示校验矩阵 H 中的一个子矩阵。 短循环对于矩阵性能的影响: 在 LDPC 码的译码算法中,我们都 假设传递的消息满足彼此独立的假设。当 H 矩阵中存在长度为 2L 的 环路时,则这些消息只在前 L 轮迭代过程中满足独立性假设(注意: 解码的迭代过程包括一次比特节点更新和一次校验节点更新)。因此 短循环的存在会影响 LDPC 码的解码性能。 另外简单的解释:例如在图 2 所示的 H 矩阵中,存在一个 4 循环 于是这个 4 循环对应的校验方程为: 11245 rxxxx =+++ 2 1356 r xxxx =+++ 由于 4 循环的存在,我们可以看到,上面两个校验方程含有共同 的比特节点 x1 与 x5,直观地说,如果这两个校验方程均出错,则我

们无法确定x1与x5中究竞哪个出错,所以从这个角度也可以说明短 循环对于性能带来的影响。 8.4LDPC码的编码方法 LDPC码属于线性分组码,利用其校验矩阵H可以生成编码矩阵G, 从而可以生成码字,其校验矩阵H可以体现LDPC码的特点与性能, 所以我们首先介绍H矩阵的构造方法。 8.4.1LDPC码校验矩阵H的构造 Gallager的H矩阵构造方法 ·每一行有j个1;一—满足行重要求 ·每一列有k个1;一一满足列重要求 ●任意两列具有共同1的个数不大于1;一满足gith值大于4 ●j和k分别与H矩阵中的列数和行数相比小得多;一一满足H 矩阵的稀疏性 设矩阵H为: Ho= 利用Ho,我们可以通过列交换的方法得到校验矩阵H: π(Ho) H= π2(H) .: π(H)】 例如下图就是由这种方法构造出的校验矩阵:
们无法确定 x1与 x5中究竟哪个出错,所以从这个角度也可以说明短 循环对于性能带来的影响。 8.4 LDPC 码的编码方法 LDPC 码属于线性分组码,利用其校验矩阵 H可以生成编码矩阵 G, 从而可以生成码字,其校验矩阵 H 可以体现 LDPC 码的特点与性能, 所以我们首先介绍 H 矩阵的构造方法。 8.4.1 LDPC 码校验矩阵 H 的构造 Gallager 的 H 矩阵构造方法 每一行有 j 个 1;——满足行重要求 每一列有 k 个 1;——满足列重要求 任意两列具有共同 1 的个数不大于 1;——满足 girth 值大于 4 j 和 k 分别与 H 矩阵中的列数和行数相比小得多;——满足 H 矩阵的稀疏性 设矩阵 H0为: 0 11...1 11...1 11...1 H = j { j { j { 利用 H0,我们可以通过列交换的方法得到校验矩阵 H: 1 0 2 0 0 ( ) ( ) ( ) k H H H π π π = H 例如下图就是由这种方法构造出的校验矩阵:

1111000000000000000 0000111100000000000 0000000011110000000 0 00000000000011110000 00000000000000001111 10001000100010000000 01000100010000001000 H=00100010000001000100 00010000001000100010 00000001000100010001 10000100000100000100 01000010001000010000 00100001000010000010 00010000100001001000 00001000010000100001 Mackay的构造方法 此方法中,校验矩阵的列重为,每行的平均重量为k(即此方法 所构造出的H矩阵),且任意两列具有共同1的个数不大于1(保证 不存在4循环)。 构造法1A 这是一种基本的构造方法,每一列具有固定的列重j。随机构造矩 阵,使其平均行重为k,且任意两列具有共同1的个数不大于1。构 造矩阵如图3所示: 3 3 图3(=3,k=6,R=1/2)
11110000000000000000 00001111 000000000000 000000001111 00000000 0000000000001111 0000 00000000000000001111 1 0001 0001 0001 0000000 01 0001 0001 0000001 000 001 0001 0000001 0001 00 0001 0000001 0001 0001 0 00000001 0001 0001 00 H = 0 1 1 00001 000001 000001 00 01 00001 0001 00001 0000 001 00001 00001 000001 0 0001 00001 00001 001 000 00001 00001 00001 00001 Mackay 的构造方法 此方法中,校验矩阵的列重为 j,每行的平均重量为 k(即此方法 所构造出的 H 矩阵),且任意两列具有共同 1 的个数不大于 1(保证 不存在 4 循环)。 构造法 1A 这是一种基本的构造方法,每一列具有固定的列重 j。随机构造矩 阵,使其平均行重为 k,且任意两列具有共同 1 的个数不大于 1。构 造矩阵如图 3 所示: 3 3 图 3(j=3,k=6,R=1/2)