中国科学技术大学：《编码理论》课程教学资源（课件讲义）第二章 基础理论

本章内容 >第二章基础理论 >2.1信道编码定理 >2.2硬判决与软判决 >2.3基本信道模型及其信道容量 >2.4MAP与ML算法 >2.5因子图与和积算法 2

本章内容  第二章 基础理论  2.1 信道编码定理  2.2 硬判决与软判决  2.3 基本信道模型及其信道容量  2.4 MAP与ML算法  2.5 因子图与和积算法 2

2.1信道编码定理 >信道编码定理：对于一个有噪信道，信道容量为C,只要数 据传输速率R根据信息论，信道容量是由输入和输出的最大互信息量决定 的，即C=maxI(X,Y) p(x) 其中X和Y分别代表信道的输入和输出；p(x)是X的概率密度 函数；IX,Y)为变量X和Y的互信息，其定义将根据具体信道 类型(BSC、AWGN等)的不同有所区别。 3

2.1 信道编码定理  信道编码定理：对于一个有噪信道，信道容量为C，只要数 据传输速率R<C，总会存在一种编码方法，使编码错误概率 p随着码长n的增加，按指数下降到任意小的值（用最大似然 译码）。即可以通过编码使通信过程实际上不发生错误，或 使错误控制在允许的数值下。  根据信息论，信道容量是由输入和输出的最大互信息量决定 的，即 其中X和Y分别代表信道的输入和输出；p(x)是X的概率密度 函数；I(X,Y)为变量X和Y的互信息，其定义将根据具体信道 类型（BSC、AWGN等）的不同有所区别。 ( ) max ( , ) p x C I X Y  3

2.2硬判决和软判决 >假设X和Y分别为q元符号和Q元符号，对于离散信道，输入 变量X和输出变量Y之间的互信息IX,Y)定义为： 1x,D=22px,)p0y1x)1o8. p(yx,) j=0i=0 p(y) 对上式取最大值，就得到硬判决的信道容量Chard。当输入输 出均为二元离散符号时，信道就可以用BSC模型来描述。 >若系统采用软判决译码，信道译码器的输入为连续值，即 y∈（∞，+∞），则信道等效为离散输入连续输出信道，X和 Y之间的互信息IX,Y)为： 1X,Y)）=∑p0x,)pyx,)log p(yx) p(y) 其中p(yk)表示发送x时解调器输出y的概率密度函数。对上 式取最大值，就得到软判决时的信道容量Co

2.2 硬判决和软判决  假设X和Y分别为q元符号和Q元符号，对于离散信道，输入 变量X和输出变量Y之间的互信息I(X,Y)定义为： 对上式取最大值，就得到硬判决的信道容量Chard。当输入输 出均为二元离散符号时，信道就可以用BSC模型来描述。  若系统采用软判决译码，信道译码器的输入为连续值，即 ，则信道等效为离散输入连续输出信道，X和 Y之间的互信息I(X,Y)为： 其中p(y|xj )表示发送xj时解调器输出y的概率密度函数。对上 式取最大值，就得到软判决时的信道容量Csoft。 1 1 2 0 0 ( | ) ( , ) ( ) ( | )log ( ) q Q i j j i j j i i p y x I X Y p x p y x p y       y   ( , )1 2 0 ( | ) ( , ) ( ) ( | )log ( ) q j j j j p y x I X Y p x p y x dy p y      4

2.3基本信道模型及其信道容量 2.3.1BSC信道 1-p >设传错概率为p,二进制对称信道(BSc)模型为： 其信道容量为： ()p.los.1+plog,(p)+-plo.(1-) j=0i=0 p(y) 我们知道，对于一个集合X,其熵为：H(X)=∑p(x)log 因此，BSC的信道容量为：C=maxI(X,Y)=1-H(p) p(x) 即每个信息比特携带1一H(p)的信息。若采用码率为R的编码，在传输错 误概率为p时，每个码字比特携带的信息量为R(1-H(p),它不能超过信道 容量，因此有： C R(1-H(p)≤C→R≤ 1-H(p) 张忠培等著，《现代编码理论与应用》，国防工业出版社，2007 5

2.3 基本信道模型及其信道容量 我们知道，对于一个集合X，其熵为： 因此，BSC的信道容量为： 即每个信息比特携带1－H(p)的信息。若采用码率为R的编码，在传输错 误概率为p时，每个码字比特携带的信息量为R(1-H(p))，它不能超过信道 容量，因此有： 0 1 0 p 1 p 1-p 1-p 1 1 2 2 2 ( ) 0 0 ( | ) max ( , ) ( ) ( | )log 1 log ( ) (1 )log (1 ) ( ) i j j i j p x j i i p y x C I X Y p x p y x p p p p   p y          1 ( ) ( )log x X ( ) H X p x  p x   ( ) max ( , ) 1 ( ) p x C I X Y H p    (1 ( )) 1 ( ) C R H p C R H p      5 张忠培等著，《现代编码理论与应用》，国防工业出版社，2007  设传错概率为p，二进制对称信道(BSC)模型为： 其信道容量为： 2.3.1 BSC信道

>对于AWGN信道，采用BPSK调制时BSC信道传输错误概率p为： -震 >若要卫→0，则实际信噪比只需大于R→0时的信噪比（临界点） 即可。 liml-p》=lmS=lim 1+plog2(p)+(1-p)log2(1-p) 进行求导 p->0 R0RR→0 R ln(p)的导数为p'1p】 lo.2o.(-P)+) > 错误概率p腿一个0函数，()-2元e”小，其导数为： -REb b一e No 2VπRWo 6

 对于AWGN信道，采用BPSK调制时BSC信道传输错误概率p为：  若要 ，则实际信噪比只需大于 时的信噪比（临界点） 即可。  由于  错误概率p是一个Q函数， ，其导数为： 6 0 0 2 2 E RE s b p Q Q N N                   p 0 R 0 2 2 0 0 0 2 2 0 1 log ( ) (1 )log (1 ) lim(1 ( )) lim lim 1 1 lim log ( ) log (1 ) (1 ) ( ) (ln 2) ( ln( ) / ln 2)(1 ) p R R R C p p p p H p R R p p p p p p p p p p    p p p                                  进行求导 的导数为 0 0 0 2 1 lim lim 2 b R R RE p Q   N           2 1 / 2 ( ) 2 y x Q x e dy      0 0 1 2 REb Eb N p e RN    

>这样 lim C 2E6 R>0R πln(2)No 实现无差错传输时，p=0,从而H(b)=0,因此 SNR E=πln(2）=0.37dB No2 即只有在信道SNR大于0.37B时才能实现无错传输，该值称为BSC信道 的Shannon限。 7

 这样 实现无差错传输时，p＝0，从而H(b)＝0，因此 即只有在信道SNR大于0.37dB时才能实现无错传输，该值称为BSC信道 的Shannon限。 7 0 0 2 lim ln(2) b R C E  R N   0 ln(2) 0.37 2 Eb SNR dB N    

2.8.2及w仔N信道的容量 >连续输入、连续输出AWGN信道容量 >带限AWGN信道的信道容量公式为： Ci log.log. 其中W为信道带宽，噪声的双边功率谱密度为N/2。 当编码速率为R,信息比特能量为E时，有 当W→oo时，得到Shannon限的渐近值为： SNR= E≥lim RW-1 C/W =In2=-1.6dB 即只有当SNR不小于一1.6dB时才可能实现无错传输，这就是理想情 况下AWGN信道的Shannon限。 8

2.3.2 AWGN信道的容量  连续输入、连续输出AWGN信道容量  带限AWGN信道的信道容量公式为： 其中W为信道带宽，噪声的双边功率谱密度为N0 /2。 当编码速率为R，信息比特能量为Eb时，有 当 时，得到Shannon限的渐近值为： 即只有当SNR不小于－1.6dB时才可能实现无错传输，这就是理想情 况下AWGN信道的Shannon限。 2 2 0 log 1 log 1 S S C W W N N W                 2 0 log 1 C REb W N W         W   / 0 2 1 lim ln 2 1.6 / R W b W E SNR dB N C W        8

>对于带限信道上的二元符号而言，在满足Nyquist的理想情况下(W =1/2T),S=REh/T,T为符号周期，AWGN信道的信道容量（每符 号所承载的信息量)为： C'=C·T=W.Tl1og2 RE。 1+ 2RE NWT N 可得 ≥ 2R-1 No 2R 当R=1/2时，Shannon容量限为0dB。 9

 对于带限信道上的二元符号而言，在满足Nyquist的理想情况下（W ＝1/2T），S=REb /T，T为符号周期，AWGN信道的信道容量（每符 号所承载的信息量）为： 则由 ，可得 当R＝1/2时，Shannon容量限为0dB。 2 2 2 0 0 1 1 2 log 1 log 1 log 1 2 2 S RE RE b b C C T W T N N WT N                             2 0 1 2 log 1 2 REb R C N           2 0 2 1 2 R Eb N R   9

>输入离散、输出连续AWGN信道容量 >输入为二元符号，电平幅度为±√E,，与BSC类似，只有在输入符 号等概时才能使互信息值达到最大，即信道容量。此时输入符号的概 率密度函数为px)=2((x+VE)+6x-VE)。 >设y()=x(t)+n(),其中n()服从均值为0、方差为o2=NJ2的高斯分 布，x)±√E,，条件概率密度函数为： 左 >根据信道容量定义，有： AWGN信道模型 C=max I(X,Y)=max(H(X)-H(XY)) p(x) p(x） H(X)=->p(x)log2 p(x)=1 10

 输入离散、输出连续AWGN信道容量  输入为二元符号，电平幅度为 ，与BSC类似，只有在输入符 号等概时才能使互信息值达到最大，即信道容量。此时输入符号的概 率密度函数为 。  设y(t)=x(t)+n(t)，其中n(t)服从均值为0、方差为 ＝N0 /2的高斯分 布，x(t)= ，条件概率密度函数为：  根据信道容量定义，有： 10  E s 2   E s     2 2 1 | exp 2 2 s s y E p y x E                   ( ) ( ) max ( , ) max ( ) ( | ) p x p x C I X Y H X H X Y    2 ( ) ( )log ( ) 1 x H X p x p x          1 ( ) 2 s s p x x E x E        0 ( ) 0, 2 N n t N       X E   s y t( ) ,      AWGN信道模型

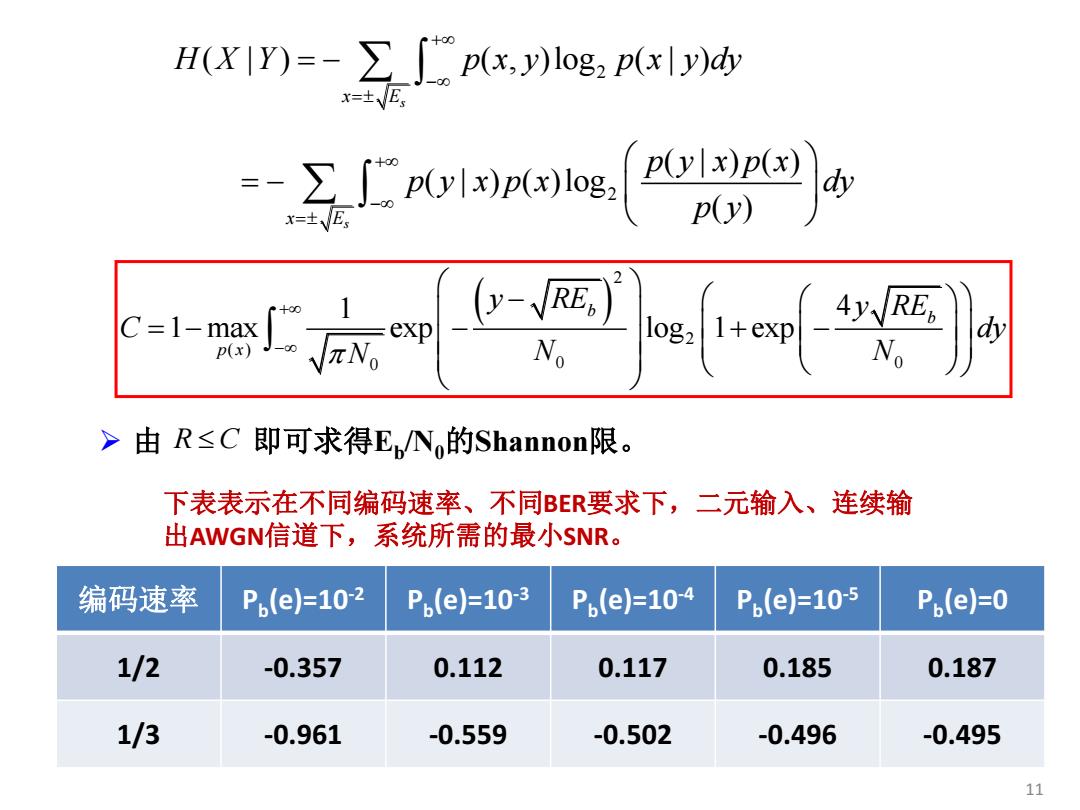
H(X Y)=->p(x,y)log2 p(xly)dy x=±E, =-∑Jp0川p(xloe p(Yx)p(x) =±E p(y) dy C-1-mg5 N (y- dy p(x) > 由R≤C即可求得E,N,的Shannon限。 下表表示在不同编码速率、不同BER要求下，二元输入、连续输 出AWGN信道下，系统所需的最小SNR。 编码速率 P.,e=10-2 P,e=103 P,(e=10-4 P,e=10-5 P.(e=0 1/2 -0.357 0.112 0.117 0.185 0.187 1/3 -0.961 -0.559 -0.502 -0.496 -0.495 11

 由 即可求得Eb /N0的Shannon限。 11 2 2 ( | ) ( , )log ( | ) ( | ) ( ) ( | ) ( )log ( ) s s x E x E H X Y p x y p x y dy p y x p x p y x p x dy p y                         2 2 ( ) 0 0 0 1 4 1 max exp log 1 exp b b p x y RE y RE C dy  N N N                                    R C 编码速率 Pb (e)=10-2 Pb (e)=10-3 Pb (e)=10-4 Pb (e)=10-5 Pb (e)=0 1/2 -0.357 0.112 0.117 0.185 0.187 1/3 -0.961 -0.559 -0.502 -0.496 -0.495 下表表示在不同编码速率、不同BER要求下，二元输入、连续输 出AWGN信道下，系统所需的最小SNR