
第五章几何对象与变换 酒中国斜学术大室 University of Science and Technology of China 5.1几何 5.2表示 5.3变换
第五章 几何对象与变换 5.1 几何 5.2 表示 5.3 变换 2

5.1几何 中国斜草技术大学 University of Science and Technology of Chin ·与坐标无关的几何 ·仿射空间 一标量 一向量 一点 ·基本几何图元 一线段 一多边形
5.1 几何 • 与坐标无关的几何 • 仿射空间 – 标量 – 向量 – 点 • 基本几何图元 – 线段 – 多边形 3

基本几何要素 中国学我术大草 University of Science and Technology of China ·几何研究n维空间中对象之间的关系 一在计算机图形学中,我们对三维空间中的对象 感兴趣 ·希望得到一个几何形状的最小集合,根据 这个集合可以建立起更复杂的对象 ·需要三个基本元素 一标量 一向量 一点
基本几何要素 • 几何研究n维空间中对象之间的关系 – 在计算机图形学中,我们对三维空间中的对象 感兴趣 • 希望得到一个几何形状的最小集合,根据 这个集合可以建立起更复杂的对象 • 需要三个基本元素 – 标量 – 向量 – 点 4
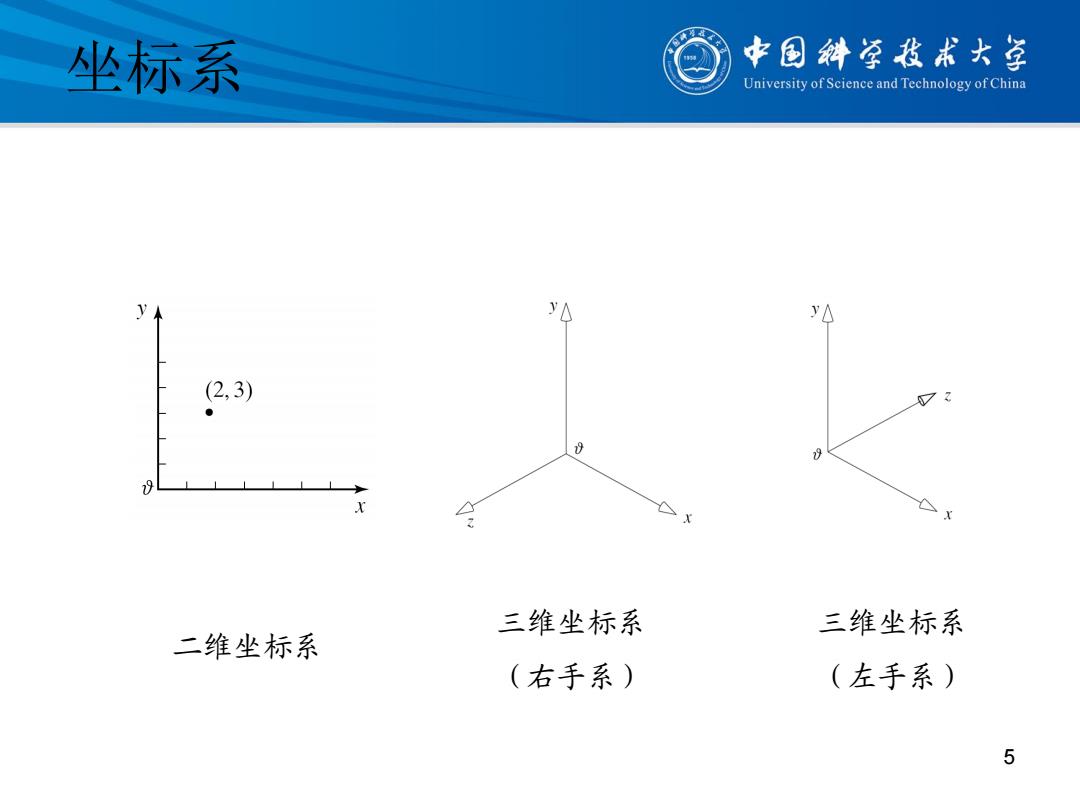
坐标系 中国斜草我术大草 University of Science and Technology of China .3 三维坐标系 三维坐标系 二维坐标系 (右手系) (左手系)
坐标系 5 二维坐标系 三维坐标系 (右手系) 三维坐标系 (左手系)

与坐标无关的几何 中国斜学我术大草 University of Scie ·在初等解析几何中,主要应用的是直角坐 标系(笛卡尔坐标系) -点在空间中的位置是p=(仪,y,z) 一通过对这些坐标进行代数运算导出结果 ·这种方法不是基于物理的 一从物理的角度来讲,点的存在性是与坐标系的 具体位置无关的 一绝大多数几何结果是不依赖于坐标系的 一例如,在欧氏几何中,两个三角形全等是指它 们有两个对应边和夹角相等
与坐标无关的几何 • 在初等解析几何中,主要应用的是直角坐 标系(笛卡尔坐标系) – 点在空间中的位置是p = (x,y,z) – 通过对这些坐标进行代数运算导出结果 • 这种方法不是基于物理的 – 从物理的角度来讲,点的存在性是与坐标系的 具体位置无关的 – 绝大多数几何结果是不依赖于坐标系的 – 例如,在欧氏几何中,两个三角形全等是指它 们有两个对应边和夹角相等 6

标量 中国斜学我术大学 University of Science and Technology of China ·在几何中需要三个基本元素 一标量、向量、点 ·标量可以定义为集合中的成员,集合中具有两 种运算:加法和乘法 一两种运算满足交换律、结合律、分配律 -加法单位元(0)和乘法单位元(1) 一加法逆元和乘法逆元(隐含定义了减法和除法) ·例:实数或复数全体,通常的加法与乘法 ·标量自身没有几何属性 7
标量 • 在几何中需要三个基本元素 – 标量、向量、点 • 标量可以定义为集合中的成员,集合中具有两 种运算:加法和乘法 – 两种运算满足交换律、结合律、分配律 – 加法单位元(0)和乘法单位元(1) – 加法逆元和乘法逆元(隐含定义了减法和除法) • 例:实数或复数全体,通常的加法与乘法 • 标量自身没有几何属性 7

为什么需要向量? 中国斜学我术大学 University of Science and Technology of China 场景:树与照相机 ·照相机需要在视平 面上形成一幅图像 表示这棵树。视平 面上哪些点需要被 激活? ·透视投影需要利用 向量来构造 视平面 10
为什么需要向量? 场景:树与照相机 • 照相机需要在视平 面上形成一幅图像 表示这棵树。视平 面上哪些点需要被 激活? • 透视投影需要利用 向量来构造 10 视平面
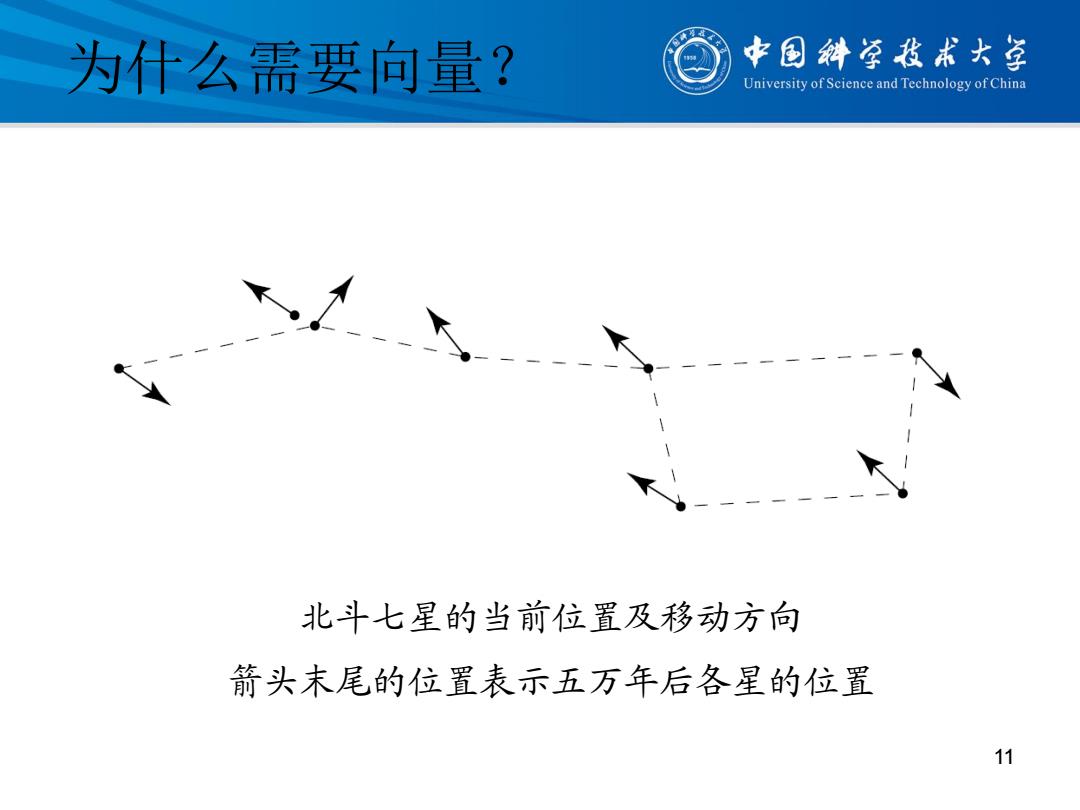
为什么需要向量? 中国斜草技术大学 niversity of Science and Technology of China 北斗七星的当前位置及移动方向 箭头末尾的位置表示五万年后各星的位置 11
为什么需要向量? 北斗七星的当前位置及移动方向 箭头末尾的位置表示五万年后各星的位置 11

向量 中国斜学我术大草 University of Science and Technology of China ·物理定义:向量是具有如下两种属性的量 一方向 -大小或长度: ·例: 一力 一速度 一有向线段 ·这也是图形学中最重要的例子 ·可以对应到其它类型上 ·用小写字母表示 12
向量 • 物理定义:向量是具有如下两种属性的量 – 方向 – 大小或长度: |v| • 例: – 力 – 速度 – 有向线段 • 这也是图形学中最重要的例子 • 可以对应到其它类型上 • 用小写字母表示 v 12
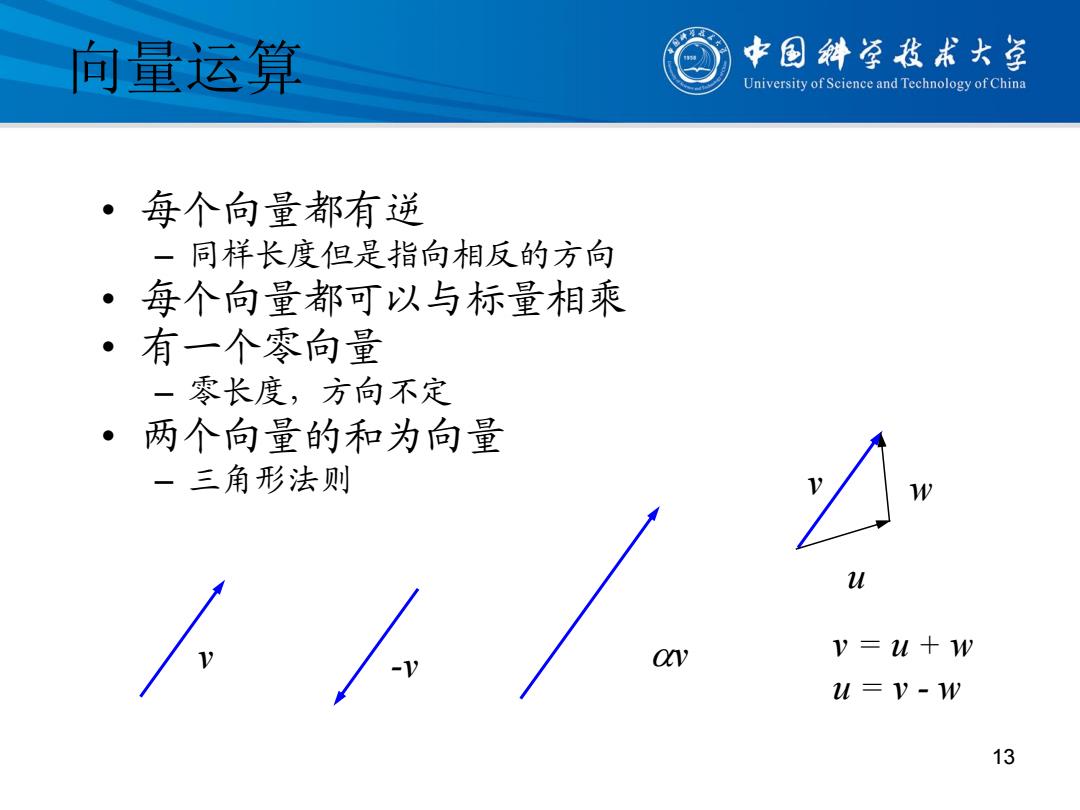
向量运算 中国斜学我术大室 University of Science and Technology of China ·每个向量都有逆 一同样长度但是指向相反的方向 ·每个向量都可以与标量相乘 ·有一个零向量 一零长度,方向不定 ·两个向量的和为向量 一三角形法则 v=u+w u=V-w 13
向量运算 • 每个向量都有逆 – 同样长度但是指向相反的方向 • 每个向量都可以与标量相乘 • 有一个零向量 – 零长度,方向不定 • 两个向量的和为向量 – 三角形法则 v -v v v u w v = u + w u = v - w 13