
"Magnetic Physics"Course Syllabus 《磁性物理学(英文)》课程教学大纲 1. Basic Information Name Magnetic Physics Course Code PHYS3116 Course Category Required course Majors Physics Credit Total Hours36 Tianyi Cai(蔡田怡) Instructors 2021.9 Sheng Ju(唯胜) Date Textbooks Magnetism in Condensed Matter,Stephen Blundell,Oxford University Press,2001 1I.Teaching aim 1)Overall objectives: This course will introduce the fundamental concepts that underly the practical use of magnetic materials. The interesting gnetic effects found in condensed matter systems have two crucial ingredients:first,that atoms should possess magnetic moments and second,that these moments should somehow interact. We will discuss the different types of magnetic materials,and the basic energies that drive their physical behaviors.A particular focus will also be on the dynamic properties of magnetic materials and their interactions with electrical excitations.These concepts will be reinforced via a micromagnetic simulation project,which allows to directly explore the intricate interplay between different magnetic interactions.The course will discuss these magnetic phenomena in the context of different applications,ranging from biomedical applications to current information technologies.At the same time,we will discuss frontiers of magnetis research,which will be reinforced through the literature revie of recently published results. 2)Course objectives: 1.Understand the key concepts of magnetic physics: 2.Know properties and applications to demonstrate the implications of all
“Magnetic Physics” Course Syllabus 《磁性物理学(英文)》课程教学大纲 I. Basic Information Name Magnetic Physics Course Code PHYS3116 Course Category Required course Majors Physics Credit 2 Total Hours 36 Instructors Tianyi Cai(蔡田怡) Sheng Ju(雎胜) Date 2021.9 Textbooks Magnetism in Condensed Matter, Stephen Blundell, Oxford University Press, 2001 II. Teaching aim 1) Overall objectives: This course will introduce the fundamental concepts that underly the practical use of magnetic materials. The interesting magnetic effects found in condensed matter systems have two crucial ingredients: first, that atoms should possess magnetic moments and second, that these moments should somehow interact. We will discuss the different types of magnetic materials, and the basic energies that drive their physical behaviors. A particular focus will also be on the dynamic properties of magnetic materials and their interactions with electrical excitations. These concepts will be reinforced via a micromagnetic simulation project, which allows to directly explore the intricate interplay between different magnetic interactions. The course will discuss these magnetic phenomena in the context of different applications, ranging from biomedical applications to current information technologies. At the same time, we will discuss frontiers of magnetism research, which will be reinforced through the literature review of recently published results. 2) Course objectives: 1. Understand the key concepts of magnetic physics; 2. Know properties and applications to demonstrate the implications of all
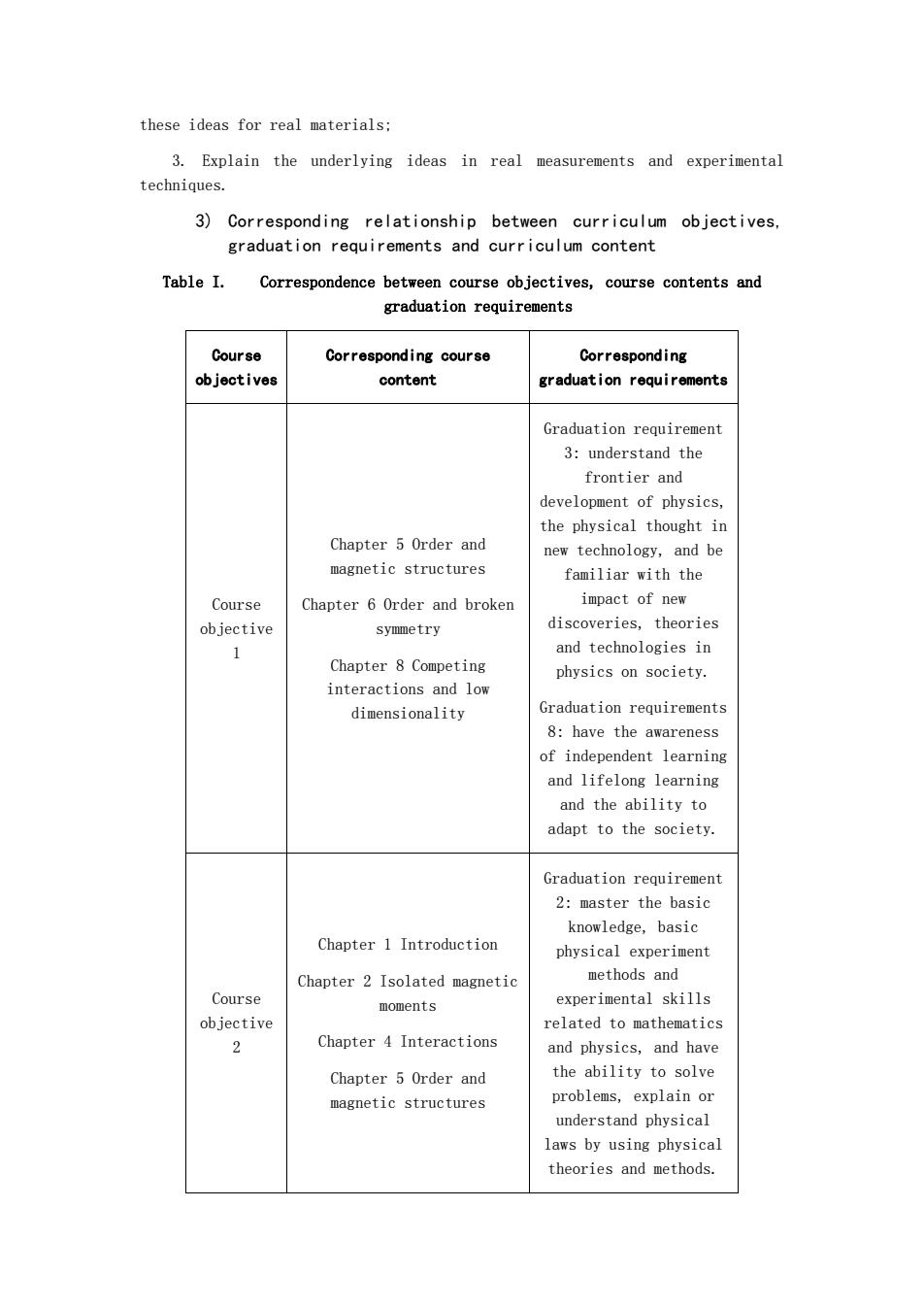
these ideas for real materials: 3.Explain the underlying ideas in real measurements and experimental techniques. 3)Corresponding relationship between curriculum objectives. graduation requirements and curriculum content Table I. Correspondence between course objectives,course contents and Course Corresponding course Corresponding ob jectives content graduation requirements Graduation requirement 3:understand the frontier and development of physics. the physical thought in Chapter 5 Order and new technology,and be magnetic structures familiar with the Course Chapter 6 Order and broker i回bact of new objective discoveries theories symmetry 1 and technologies in Chapter 8 Competing physics on society. interactions and low dimensionality Graduation requirements 8:have the awareness of independent learning and lifelong learning and the ability to adapt to the society. Graduation requiremen 2:master the basic knowledge,basic Chapter 1 Introduction physical experiment Chapter 2 Isolated magneti methods and Course experimental skills moments ob jective related to mathematics 2 Chapter 4 Interactions and physics,and have Chapter 5 Order and the ability to solve magnetic structures problems,explain or understand physical laws by using physical theories and methods
these ideas for real materials; 3. Explain the underlying ideas in real measurements and experimental techniques. 3) Corresponding relationship between curriculum objectives, graduation requirements and curriculum content Table I. Correspondence between course objectives, course contents and graduation requirements Course objectives Corresponding course content Corresponding graduation requirements Course objective 1 Chapter 5 Order and magnetic structures Chapter 6 Order and broken symmetry Chapter 8 Competing interactions and low dimensionality Graduation requirement 3: understand the frontier and development of physics, the physical thought in new technology, and be familiar with the impact of new discoveries, theories and technologies in physics on society. Graduation requirements 8: have the awareness of independent learning and lifelong learning and the ability to adapt to the society. Course objective 2 Chapter 1 Introduction Chapter 2 Isolated magnetic moments Chapter 4 Interactions Chapter 5 Order and magnetic structures Graduation requirement 2: master the basic knowledge, basic physical experiment methods and experimental skills related to mathematics and physics, and have the ability to solve problems, explain or understand physical laws by using physical theories and methods

Graduation requirements 8:have the awareness of independent learnin and lifelong learning and the ability to adapt to the society. Graduation requiremen 2:master the basic knowledge,basic physical experiment methods and experimental skills related to mathematics and physics,and hav the ability to solve problems,explain or Chapter 3 Environments understand physical Course Chapter 4 Interaction laws by using physical objective theories and methods Chapter 7 Magnetism in metals Graduation requirements 7:have the ability of sub iect research. Graduation requirements 8:have the awareness of independent learning and lifelong learning and the ability to adapt to the society. 1II.Contents Chapter One:Introduction 1.Teaching aims Understand the concept of magnetic moments:
Graduation requirements 8: have the awareness of independent learning and lifelong learning and the ability to adapt to the society. Course objective 3 Chapter 3 Environments Chapter 4 Interaction Chapter 7 Magnetism in metals Graduation requirement 2: master the basic knowledge, basic physical experiment methods and experimental skills related to mathematics and physics, and have the ability to solve problems, explain or understand physical laws by using physical theories and methods. Graduation requirements 7: have the ability of subject research, design, data processing and academic exchange. Graduation requirements 8: have the awareness of independent learning and lifelong learning and the ability to adapt to the society. III. Contents Chapter One: Introduction 1. Teaching aims Understand the concept of magnetic moments;

Explain some facts about magnetic moments from elementary classical and quantum physics 2.Keypoints and Difficulties Keypoints:Magnetic moments Difficulties:The classical and quantum understanding of the magnetic moments 3.Contents 1.1 Magnetic moments 1.1.1 Magnetic moments and angular momentum 1.1.2 Precession 1.1.3 The Bohr magneton 1.1.4 Magnetization and field 1.2 Classical mechanics and magnetic moments 1.2.1 Canonical momentum 1.2.2 The Bohr-van Leeuwen theorem 1.3 Quantum mechanics of spin 1.3.1 Orbital and spin angular momentum 1.3.2 Pauli spin matrices and spinors 1.3.3 Raising and lowering operators 1.3.4 The coupling of two spins 4.Teaching method Teaching:Group Discussion:Autodidacticism under the guidance of the teacher 5.Comments Carefully prepare lessons,prepare students and make preparations before class:In the teaching process,we pay attention to cultivating students' creative thinking,take students as the main body and enhance students'sense of participation:Corresponding exercises and supplementary exercises after class. Problems: (1.1)Calculate the magnetic moment of an electron (with g=2).What is the Larmor precession frequency of this electron in a magnetic field of flux density 0.3 T?What is the difference in energy of the electron if its spin
Explain some facts about magnetic moments from elementary classical and quantum physics 2. Keypoints and Difficulties Keypoints: Magnetic moments Difficulties: The classical and quantum understanding of the magnetic moments 3. Contents 1.1 Magnetic moments 1.1.1 Magnetic moments and angular momentum 1.1.2 Precession 1.1.3 The Bohr magneton 1.1.4 Magnetization and field 1.2 Classical mechanics and magnetic moments 1.2.1 Canonical momentum 1.2.2 The Bohr-van Leeuwen theorem 1.3 Quantum mechanics of spin 1.3.1 Orbital and spin angular momentum 1.3.2 Pauli spin matrices and spinors 1.3.3 Raising and lowering operators 1.3.4 The coupling of two spins 4.Teaching method Teaching; Group Discussion; Autodidacticism under the guidance of the teacher 5.Comments Carefully prepare lessons, prepare students and make preparations before class; In the teaching process, we pay attention to cultivating students' creative thinking, take students as the main body and enhance students' sense of participation; Corresponding exercises and supplementary exercises after class. Problems: (1.1) Calculate the magnetic moment of an electron (with g = 2). What is the Larmor precession frequency of this electron in a magnetic field of flux density 0.3 T? What is the difference in energy of the electron if its spin

points parallel or antiparallel to the magnetic field?Convert this energy into a frequency. (1.2)Using the definition of spin operators in eqn 1.43.prove eqn 1.53 and the commutation relations,egns 1.54 and 1.55. (1.3)Using the definition of the raising and lowering operators in eans 1.57, prove eans 1.58.1.61. (1.)Using the commutation relation for spin,namely that [,5l=i (and cyclic permutations),prove that [6.XS=i×X, where X is a vector. (1.5)Using eqns 1.58 and 1.61,show that S±lS,S)=√SS+I)-Sz(S2±S,S2±1. where \S,SZ>represents a state with total spin angular momentum S(S+ 1)h2 and z component of spin angular momentum Szh.Hence prove the following special cases of eqn 1.76: 5-1S,5)=√2S1S,S-1) 5+lS,S-1)=√2S1S.S (1.6)The kinetic energy operator for an electron is p2/2m.Use ean 1.41 to show that this can be rewritter (o·)2 2me If a magnetic field is applied one must replace p by p +eA.With the aid of ean 1.40,show that this replacement substituted into eqn 1.79 leads to kinetic energy of the form (+eA)2 2me +8uBB.S where the g-factor in this case is g=2.(Note that in this problem you have to be careful how you apply eqn 1.40 and 1.41 because p is an operator and will not commute with A.)
points parallel or antiparallel to the magnetic field? Convert this energy into a frequency. (1.2) Using the definition of spin operators in eqn 1.43, prove eqn 1.53 and the commutation relations, eqns 1.54 and 1.55. (1.3) Using the definition of the raising and lowering operators in eqns 1.57, prove eqns 1.58, 1.61. (1.4) Using the commutation relation for spin, namely that (and cyclic permutations), prove that where X is a vector. (1.5) Using eqns 1.58 and 1.61, show that where \S, SZ> represents a state with total spin angular momentum S(S + l)h2 and z component of spin angular momentum Szh. Hence prove the following special cases of eqn 1.76: (1.6) The kinetic energy operator for an electron is p2/2m. Use eqn 1.41 to show that this can be rewritten If a magnetic field is applied one must replace p by p +eA. With the aid of eqn 1.40, show that this replacement substituted into eqn 1.79 leads to kinetic energy of the form where the g-factor in this case is g = 2. (Note that in this problem you have to be careful how you apply eqn 1.40 and 1.41 because p is an operator and will not commute with A.)

Chapter Two:Isolated magnetic moments 1.Teaching aims Explain the properties of isolated magnetic moments: Understand the concepts of paramagnetism and Diamagnetism; Determine the magnetic ground of 4f ions by using the Hund's rules 2.Keypoints and Difficulties Keypoints:susceptibility:paramagnetism:Diamagnetism:Hund's Rule: SC coupling:JJ coupling Difficulties:the classical and quantum theory of paramagnetism: determine the magnetic ground of 4f ions by using the Hund's rules 3.Contents 2.1 An atom in a magnetic field 2.2 Magnetic susceptibility 2.3 Diamagnetism 2.4 Paramagnetism 2.4.1 Semiclassical treatment of paramagnetism 2.4.2 Paramagnetism for J=1/2 2.4.3 The Brillouin function 2.4.4 Van Vleck paramagnetism 2.5 The ground state of an ion and Hund's rules 2.5.1Fine structure 2.5.2 Hund's rules 2.5.3 L-S and j-j coupling 4.Teaching method Teaching:Group Discussion:Autodidacticism under the guidance of the teacher 5.Comments Carefully prepare lessons,prepare students and make preparations before class:In the teaching process,we pay attention to cultivating students'creative thinking,take students as the main body and enhance students'sense of participation;Corresponding exercises and supplementary exercises after class
Chapter Two: Isolated magnetic moments 1. Teaching aims Explain the properties of isolated magnetic moments; Understand the concepts of paramagnetism and Diamagnetism; Determine the magnetic ground of 4f ions by using the Hund’s rules. 2. Keypoints and Difficulties Keypoints: susceptibility; paramagnetism; Diamagnetism; Hund’s Rule; SC coupling; JJ coupling Difficulties: the classical and quantum theory of paramagnetism; determine the magnetic ground of 4f ions by using the Hund’s rules 3. Contents 2.1 An atom in a magnetic field 2.2 Magnetic susceptibility 2.3 Diamagnetism 2.4 Paramagnetism 2.4.1 Semiclassical treatment of paramagnetism 2.4.2 Paramagnetism for J = 1/2 2.4.3 The Brillouin function 2.4.4 Van Vleck paramagnetism 2.5 The ground state of an ion and Hund's rules 2.5.1 Fine structure 2.5.2 Hund's rules 2.5.3 L-S and j-j coupling 4. Teaching method Teaching; Group Discussion; Autodidacticism under the guidance of the teacher 5. Comments Carefully prepare lessons, prepare students and make preparations before class; In the teaching process, we pay attention to cultivating students' creative thinking, take students as the main body and enhance students' sense of participation; Corresponding exercises and supplementary exercises after class

Problems: (2.1)Calculate the diamagnetic orbital susceptibility of a gas of hydrogen atoms (with number density 1020 m)in the ground state,and compare this with the entirely of water).What magnetic field would be necessary to induce the same magnetic moment in the duck as is contained in a magnetized iron filing?Repeat the calculation for a cow. (2.3)Calculate the mass 249.7 g)in a field of 1 T at 10 K. (2.4)Using the expressions for the partition function and the Helmholtz function of a spin-1/2 particle in a magnetic field B from eans 2.29 and 2.30 respectively, show that for such non-interacting particles per unit volume, the energy E pe unit volume is given by 公=-e8an(给)】 the heat capacity per unit volume is given by c(需}a(》) and the entropy per unit volume is given by s[(c(器)》-器m(e】 (2.5)Show that Hund's rules for a shell of angular momentum 1 and containing n electrons can be summarized by S=21+1-2☑+1-m L=S12l+1-m川 J=S121-nl. (2.6)Find the term symbols for the ground states of the ions (a)Ho3+(4f10), (b)Er3+(4f11),(c)Tm3+(4f12),and(d)Lu3+(4f14). Chapter Three:Environments 1.Teaching aims Understand the physical picture of the interactions between an atom and its immediate surroundings: Determine the magnetic ground of 3d ions under an octahedral or tetrahedral crystal field
Problems: (2.1) Calculate the diamagnetic orbital susceptibility of a gas of hydrogen atoms (with number density 1020 m-3) in the ground state, and compare this with the paramagnetic spin susceptibility at 100 K. (2.2) Estimate the diamagnetic susceptibility of a duck (assume it is composed entirely of water). What magnetic field would be necessary to induce the same magnetic moment in the duck as is contained in a magnetized iron filing? Repeat the calculation for a cow. (2.3) Calculate the paramagnetic moment of a crystal (with dimensions 2 mm x 2 mm x 2 mm) of CuSO4 5H2O (see Table 2.1, density 2286 kg m- 3 , relative molecular mass 249.7 g) in a field of 1 T at 10 K. (2.4) Using the expressions for the partition function and the Helmholtz function of a spin-1/2 particle in a magnetic field B from eqns 2.29 and 2.30 respectively, show that for n such non-interacting particles per unit volume, the energy E per unit volume is given by the heat capacity per unit volume is given by and the entropy per unit volume is given by (2.5) Show that Hund's rules for a shell of angular momentum l and containing n electrons can be summarized by (2.6) Find the term symbols for the ground states of the ions (a) Ho3+ (4f10), (b) Er3+ (4f11), (c) Tm3+ (4f 12), and (d) Lu3+ (4f14). Chapter Three: Environments 1. Teaching aims Understand the physical picture of the interactions between an atom and its immediate surroundings; Determine the magnetic ground of 3d ions under an octahedral or tetrahedral crystal field

2.Keypoints and Difficulties Keypoints:crystal field;orbital quenching:Jahn-Teller effects Difficulties:crystal field:orbital quenching:Jahn-Teller effects 3.Contents 3.1 Crystal fields 3.1.1 Origin of crystal fields 3.1.2 Orbital quenching 3.1.3 The Jahn-Teller effect 3.2 Magnetic resonance techniques 3.2.1 Nuclear magnetic resonance 4.Teaching method Teaching:Group Discussion:Autodidacticism under the guidance of the teacher 5.Comments Carefully prepare lessons,prepare students and make preparations before class:In the teaching process,we pay attention to cultivating students'creative thinking,take students as the main body and enhance students sense of participation:Correspondingexercises and supplementary exercises after class. Problems: (3.1)A Sc++ion has one electron in the 3d shell.It is in an anisotropic crystal and the crystal field can be written as a potential acting on the 3d electron as Al'z.What are the lowest orbital states of the Sc ion if A>0 and if A0?The spin-orbit coupling A.1s is much smaller than the crystal field When this is included,what are the approximate ground states of the ion,for A 0?Discuss the effect on these states of applying a small magnetic field along the z axis and perpendicular to the z axis,and sketch the temperature dependence of the susceptibility. (3.2)Equal point positive charges are placed on each of the six comers of an octahedron.Taking the origin of a set of cartesian coordinates to be at the centre of the octahedron,show that the potential close to the centre is given by where q is the magnitude of each charge and a is the distance between the origin and each charge
2. Keypoints and Difficulties Keypoints: crystal field; orbital quenching; Jahn-Teller effects Difficulties: crystal field; orbital quenching; Jahn-Teller effects 3. Contents 3.1 Crystal fields 3.1.1 Origin of crystal fields 3.1.2 Orbital quenching 3.1.3 The Jahn-Teller effect 3.2 Magnetic resonance techniques 3.2.1 Nuclear magnetic resonance 4. Teaching method Teaching; Group Discussion; Autodidacticism under the guidance of the teacher 5. Comments Carefully prepare lessons, prepare students and make preparations before class; In the teaching process, we pay attention to cultivating students' creative thinking, take students as the main body and enhance students' sense of participation; Corresponding exercises and supplementary exercises after class. Problems: (3.1) A Sc++ ion has one electron in the 3d shell. It is in an anisotropic crystal and the crystal field can be written as a potential acting on the 3d electron as Al2 z. What are the lowest orbital states of the Sc ion if A > 0 and if A 0? Discuss the effect on these states of applying a small magnetic field along the z axis and perpendicular to the z axis, and sketch the temperature dependence of the susceptibility. (3.2) Equal point positive charges are placed on each of the six comers of an octahedron. Taking the origin of a set of cartesian coordinates to be at the centre of the octahedron, show that the potential close to the centre is given by where q is the magnitude of each charge and a is the distance between the origin and each charge

(3.3)An ion,whose nucleus has zero nuclear spin,has a ground state comprising two degenerate levels corresponding to an effective spin S=1/2.The application of a magnetic field of flux density B produces a separation of the levels which is linear in B.A single electron paramagnetic resonance line observed fo the ion at a frequency of 30 GHz and a magnetic flux density of 0.6 T.An isotope with non-zero nuclear spin I gives rise to a hyperfine structure (described in the spin-Hamiltonian by a term AI S)comprising four approximately equally spaced resonance lines.with separation 10T.symmetrically disposed about the line due to the isotope with ze ronuclear spin.What information does this give about (a)the nuclear spin and (b)the nuclear magnetic moment of the isotope?Calculate the value of the parameter A.Why is it sometimes necessary to perform these measurements at low temperature? (3.4)An NMR spectrometer operates at a frequency of 60 MHz.At what applied to observe the resonance of H,2H,13C and 19F nuclei?(Use the data in Table 2.3.) (3.5)An ESR spectrometer operates at a frequency of 9 GHz (known as X-band). oudbe required to observe a signal fro the electron in DPPH (an calibrate ESR spectrometers which gives a sharp signal at g=2). Chapter Four:Interactions 1.Teaching aims Understand the different types of magnetic interaction 2.Keypoints and Difficulties Keypoints:Direct exchange Difficulties:Indirect exchange in ionic solids:superexchange 3.Contents 4.1 Magnetic dipolar interaction 4.2 Exchange interaction 4.2.1 Origin of exchange 4.2.2 Direct exchange 4.2.3 Indirect exchange in ionic solids:superexchange 4.2.4 Indirect exchange in metals 4.2.5 Double exchange 4.2.6 Anisotropic exchange interaction
(3.3) An ion, whose nucleus has zero nuclear spin, has a ground state comprising two degenerate levels corresponding to an effective spin S = 1/2. The application of a magnetic field of flux density B produces a separation of the levels which is linear in B. A single electron paramagnetic resonance line is observed for the ion at a frequency of 30 GHz and a magnetic flux density of 0.6 T. An isotope with non-zero nuclear spin I gives rise to a hyperfine structure (described in the spin-Hamiltonian by a term AI S) comprising four approximately equally spaced resonance lines, with separation 10-2 T, symmetrically disposed about the line due to the isotope with zero nuclear spin. What information does this give about (a) the nuclear spin and (b) the nuclear magnetic moment of the isotope? Calculate the value of the parameter A. Why is it sometimes necessary to perform these measurements at low temperature? (3.4) An NMR spectrometer operates at a frequency of 60 MHz. At what applied magnetic field would you expect to observe the resonance of 1H, 2H, 13C and 19F nuclei? (Use the data in Table 2.3.) (3.5) An ESR spectrometer operates at a frequency of 9 GHz (known as X-band). What magnetic field would be required to observe a signal from the unpaired electron in DPPH (an organic molecule used to calibrate ESR spectrometers which gives a sharp signal at g = 2). Chapter Four: Interactions 1. Teaching aims Understand the different types of magnetic interaction 2. Keypoints and Difficulties Keypoints: Direct exchange Difficulties: Indirect exchange in ionic solids: superexchange 3. Contents 4.1 Magnetic dipolar interaction 4.2 Exchange interaction 4.2.1 Origin of exchange 4.2.2 Direct exchange 4.2.3 Indirect exchange in ionic solids: superexchange 4.2.4 Indirect exchange in metals 4.2.5 Double exchange 4.2.6 Anisotropic exchange interaction

4.2.7 Continuum approximation 4.Teaching method Teaching:Group Discussion:Autodidacticism under the guidance of the teacher 5.Comments Carefully prepare lessons,prepare students and make preparations before class:In the teaching process,we pay attention to cultivating students'creative thinking,take students as the main body and enhance students'sense of participation:Corresponding exercises and supplementary exercises after class. Problems (4.1)Show that two magnetic dipoles ul and u2 separated by r have a dipolar energy equal to 3 E= 40 (4.2)Calculate the magnitude of the magnetic field 1 A and 10 A from a proton in a direction (a)parallel and (b)perpendicular to the proton spin direction. (4.3)Estimate the ratio of the exchange and dipolar coupling of two adjacent Fe atoms in metallic Fe. (The exchange constant in Fe can be c setting it equal to kTc where TC is the Curie temperature.For Fe,TC =1043 K. (4.4)Provide a rough estimate of the size of the exchange constant in a magnetic oxide which is coupled by superexchange using the measured value of the electronic bandwidth (determined by inelastic neutron scattering)of 0.05 eV.Take the Coulomb energy to be ordering temperature (4.5)Consider the case of two interacting spin-1/2 electrons.The good quantum numbers are S=0 and 1 so that there is a triplet state and a singlet state which will be separated by an energy gap A.We define the sign of A so that when A >0 the singlet state (S=0)is the lower state and A 0 the triplet state is the lower state.These situations are shown in Fig.4.6(a)and (b) Show that the susceptibility in this model is given by 2Ng43 X=kT6+eak可 which is known as the Bleaney-Bowers equation.It is plotted in Fig.4.6(c)
4.2.7 Continuum approximation 4. Teaching method Teaching; Group Discussion; Autodidacticism under the guidance of the teacher 5. Comments Carefully prepare lessons, prepare students and make preparations before class; In the teaching process, we pay attention to cultivating students' creative thinking, take students as the main body and enhance students' sense of participation; Corresponding exercises and supplementary exercises after class. Problems: (4.1) Show that two magnetic dipoles u1 and u2 separated by r have a dipolar energy equal to (4.2) Calculate the magnitude of the magnetic field 1 A and 10 A from a proton in a direction (a) parallel and (b) perpendicular to the proton spin direction. (4.3) Estimate the ratio of the exchange and dipolar coupling of two adjacent Fe atoms in metallic Fe. (The exchange constant in Fe can be crudely estimated by setting it equal to kBTc where TC is the Curie temperature. For Fe, TC =1043 K.) (4.4) Provide a rough estimate of the size of the exchange constant in a magnetic oxide which is coupled by superexchange using the measured value of the electronic bandwidth (determined by inelastic neutron scattering) of 0.05 eV. Take the Coulomb energy to be ~1 eV, Hence estimate the antiferromagnetic ordering temperature. (4.5) Consider the case of two interacting spin-1/2 electrons. The good quantum numbers are S = 0 and 1 so that there is a triplet state and a singlet state which will be separated by an energy gap A. We define the sign of A so that when A > 0 the singlet state (S = 0) is the lower state and when A < 0 the triplet state is the lower state. These situations are shown in Fig. 4.6(a) and (b). Show that the susceptibility in this model is given by which is known as the Bleaney-Bowers equation. It is plotted in Fig. 4.6(c)