
《量子力学》课程教学大纲 一、课程基本信息 英文名称Quantum Mechanics 课程代码 PHYS3004 课程性质专业必修课程 授课对象 物理学 学分4学分 学时 72学时 主讲教师 周丽萍 修订日期 2021.9 指定教材曾谨言,《量子力学教程》,科学出版社,2000年 二、课程目标 (一)总体目标: 本课程的知识目标:了解量子力学的实验基础和发据史、应用和前沿,及其对现代到学 技术的支撑作用:系统掌握量子力学的基本概念、基本原理及处理量子系统实际问的计算 方法。能力目标 掌握微观体系的物理研究方法和前沿进展,提高解决交叉学科领域量子问 题的能力,锤炼科学思维能力和科研创新能力。素质目标:掌捉辩证唯物主义基本原理,建 立科学的世界观和方法论:富有科学精神,勇于在物理学前沿及交叉领域探素、创新与攀登。 (二)课程目标: 课程目标1:了解量子力学的发展简史,量子力学理论发展中的著名物理实验及其地位 和作用:了解量子力学的诠释及适用范围:了解量子力学实验和理论研究的前沿进展和应用 前景:使学生认识到量子力学理论在现代科学研究领域的重要性,掌握辩证唯物主义基本原 理,建立科学的世界观和方法论。 课程目标2:掌握量子力学基本原理和基本计算方法,学会运用量子力学理论对一维定 态若干问题,以及: 力场 原子等问题的分析 和处 训练学生 求解并分析 量子系统的能力,培养和提高学生的抽象思维能力和解决交叉学科领域量子问题的能力。 课程目标3:掌握定态微扰论的近似计算方法,掌握利用含时微扰理论处理近代物理实 验量子跃迁等的方法,掌握自旋及全同粒子体系的处理方法:培养和提高学生对非精确求解、 自旋纠缠态等复杂系统的求解能力,掌握对近似解的误差分析和数据处理等基本技能,锤炼 科学思维能力和科研创新能力 (三)课程目标与毕业要求、课程内容的对应关系 表1:课程目标与课程内容、毕业要求的对应关系表
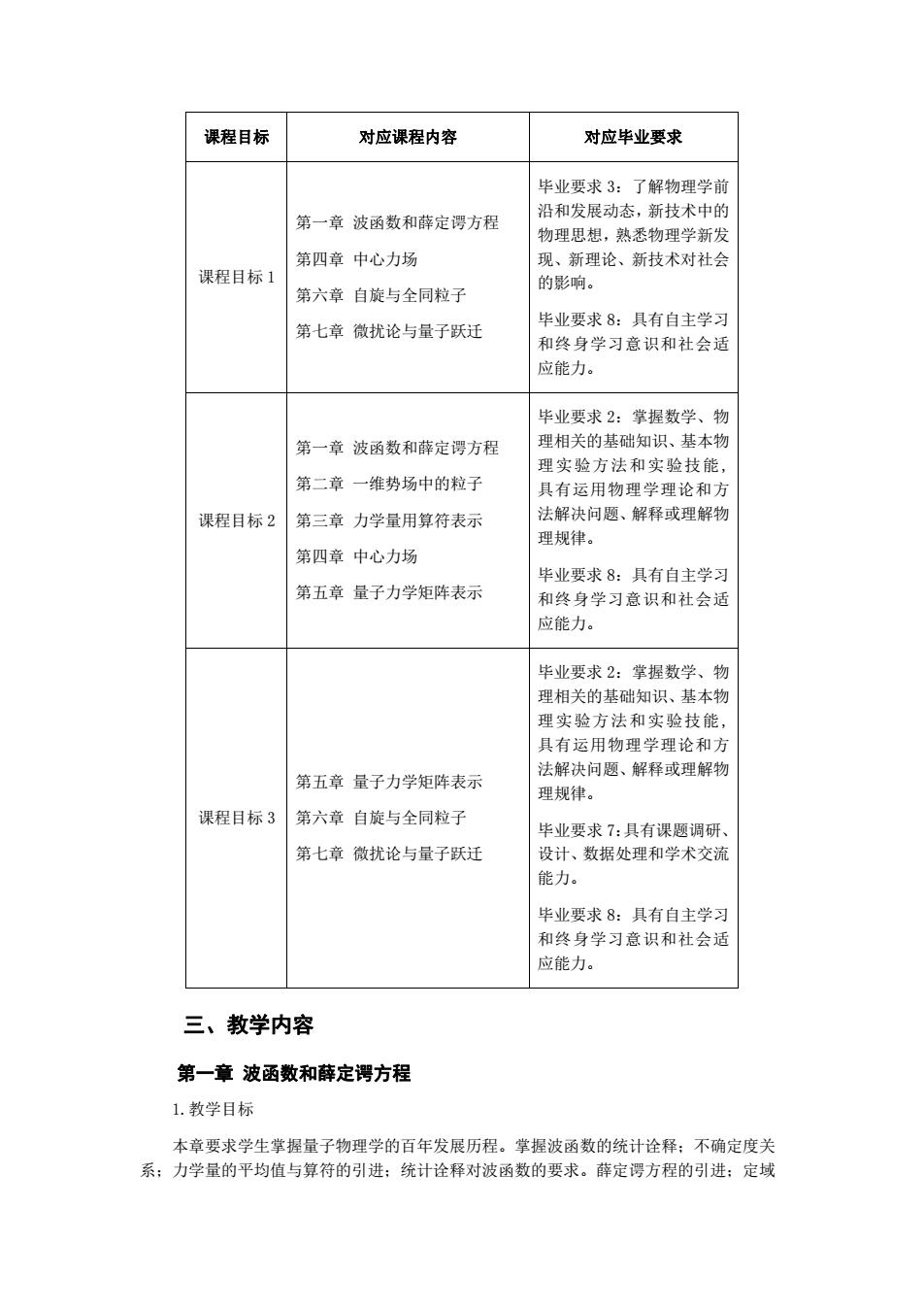
《量子力学》课程教学大纲 一、课程基本信息 英文名称 Quantum Mechanics 课程代码 PHYS3004 课程性质 专业必修课程 授课对象 物理学 学 分 4 学分 学 时 72 学时 主讲教师 周丽萍 修订日期 2021.9 指定教材 曾谨言,《量子力学教程》,科学出版社,2000 年 二、课程目标 (一)总体目标: 本课程的知识目标:了解量子力学的实验基础和发展史、应用和前沿,及其对现代科学 技术的支撑作用;系统掌握量子力学的基本概念、基本原理及处理量子系统实际问题的计算 方法。能力目标:掌握微观体系的物理研究方法和前沿进展,提高解决交叉学科领域量子问 题的能力,锤炼科学思维能力和科研创新能力。素质目标:掌握辩证唯物主义基本原理,建 立科学的世界观和方法论;富有科学精神,勇于在物理学前沿及交叉领域探索、创新与攀登。 (二)课程目标: 课程目标 1:了解量子力学的发展简史,量子力学理论发展中的著名物理实验及其地位 和作用;了解量子力学的诠释及适用范围;了解量子力学实验和理论研究的前沿进展和应用 前景;使学生认识到量子力学理论在现代科学研究领域的重要性,掌握辩证唯物主义基本原 理,建立科学的世界观和方法论。 课程目标 2:掌握量子力学基本原理和基本计算方法,学会运用量子力学理论对一维定 态若干问题,以及中心力场氢原子等问题的分析和处理;训练学生运用理论公式求解并分析 量子系统的能力,培养和提高学生的抽象思维能力和解决交叉学科领域量子问题的能力。 课程目标 3:掌握定态微扰论的近似计算方法,掌握利用含时微扰理论处理近代物理实 验量子跃迁等的方法,掌握自旋及全同粒子体系的处理方法;培养和提高学生对非精确求解、 自旋纠缠态等复杂系统的求解能力,掌握对近似解的误差分析和数据处理等基本技能,锤炼 科学思维能力和科研创新能力。 (三)课程目标与毕业要求、课程内容的对应关系 表 1:课程目标与课程内容、毕业要求的对应关系表
课程目标 对应课程内容 对应毕业要求 毕业要求3:了解物理学前 第一章波函数和薛定谔方程 沿和发展动态,新技术中的 物理思相,熟采物理学新发 第四章中心力场 现、新理论、新技术对社会 课程目标1 第六章自旋与全同粒子 的影响。 第七章微扰论与量子跃迁 毕业要求8:具有自主学习 和终身学习意识和社会适 应能力。 毕业要求2:掌握数学、物 第一章波函数和薛定谔方程 理相关的基础知识 、基本物 理实验方法和实验技能 第二章一维势场中的粒子 具有运用物理学理论和方 课程目标2 第三章力学量用算符表示 法解决间题、解释或理解物 理规律。 第四章中心力场 毕业要求8:具有自主学习 第五章量子力学矩阵表示 和终身学习意识和社会适 应能力。 毕业要求2:掌握数学、物 理相关的基础知识、基本物 理实验方法和实验技能 具有运用物理学理论和方 法解决问题、解释或理解物 第五章量子力学矩阵表示 理规律。 课程目标3 第六章自旋与全同粒子 毕业要求7:具有课题调研、 第七章微扰论与量子跃迁 设计、数据处理和学术交流 能力。 毕业要求8:且右省白主学习 和终身学习意识和社会适 应能力。 三、教学内容 第一章波函数和薛定谔方程 1.教学目标 本章要求学生掌握量子物理学的百年发展历程。掌握波函数的统计诠释:不确定度关 系:力学量的平均值与算符的引进:统计诠释对波函数的要求。薛定谔方程的引进:定域
课程目标 对应课程内容 对应毕业要求 课程目标 1 第一章 波函数和薛定谔方程 第四章 中心力场 第六章 自旋与全同粒子 第七章 微扰论与量子跃迁 毕业要求 3:了解物理学前 沿和发展动态,新技术中的 物理思想,熟悉物理学新发 现、新理论、新技术对社会 的影响。 毕业要求 8:具有自主学习 和终身学习意识和社会适 应能力。 课程目标 2 第一章 波函数和薛定谔方程 第二章 一维势场中的粒子 第三章 力学量用算符表示 第四章 中心力场 第五章 量子力学矩阵表示 毕业要求 2:掌握数学、物 理相关的基础知识、基本物 理实验方法和实验技能 , 具有运用物理学理论和方 法解决问题、解释或理解物 理规律。 毕业要求 8:具有自主学习 和终身学习意识和社会适 应能力。 课程目标 3 第五章 量子力学矩阵表示 第六章 自旋与全同粒子 第七章 微扰论与量子跃迁 毕业要求 2:掌握数学、物 理相关的基础知识、基本物 理实验方法和实验技能 , 具有运用物理学理论和方 法解决问题、解释或理解物 理规律。 毕业要求 7:具有课题调研、 设计、数据处理和学术交流 能力。 毕业要求 8:具有自主学习 和终身学习意识和社会适 应能力。 三、教学内容 第一章 波函数和薛定谔方程 1.教学目标 本章要求学生掌握量子物理学的百年发展历程。掌握波函数的统计诠释;不确定度关 系;力学量的平均值与算符的引进;统计诠释对波函数的要求。薛定谔方程的引进;定域

概率守恒:能量本征方程:定态和非定态:多粒子体系的薛定谔方程。态叠加原理,测量 与波函数的塌缩。使学生认识到量子力学理论在现代科学研究领域的重要性,掌握辩证唯 物主义基本原理,建立科学的世界观和方法论。 2.教学重难点 波粒二象性:波函数的统计诠释:算符概念:薛定谔方程 3教学内容 第一节波函数的统计诠释 一、波粒二象性 教学要点:掌握描述微观粒子运动状态的物理量:掌握波函数的性质,波函数的归 化,掌握波函数的概率解释:理解动量概率分布:初步理解不确定度关系:算符本征函数 和本征值。 二、力学量的引进 教学要点:力学量平均值计算方法,力学量算符引进,掌握哈密顿算符的书写。 三、统计诠释对波函数的要求 教学要点:理解统计诠释对波函数提出的单值、有限、连续、平方可积等要求 第二节薛定谔方程 一、薛定谔方程的引进和讨论 教学要点:对比薛定谔方程与经典牛顿方程,掌握薛定谔方程的书写:基于薛定谔方 程掌握概率流密度矢量,理解定域概率守恒定律。 二、能量本征方程 教学要点:了解能量本征方程,掌握定态概念,了解定态与非定态随时间变化的特 点。 三、多粒子体系的薛定谔方程 教学要点:掌握多粒子体系的薛定调方程的书写。 第三节量子态叠加原理 一、量子态及其表象 教学要点:初步了解表象概念,了解坐标表象和动量表象及其变换方法。 二、量子态叠加原理 教学要点:了解态叠加原理:了解量子态的测量与波函数塌缩的现象 4.教学方法 教师讲授,师生讨论,翻转课堂,指导学生自主学习等。 5.教学评价
概率守恒;能量本征方程;定态和非定态;多粒子体系的薛定谔方程。态叠加原理,测量 与波函数的塌缩。使学生认识到量子力学理论在现代科学研究领域的重要性,掌握辩证唯 物主义基本原理,建立科学的世界观和方法论。 2.教学重难点 波粒二象性;波函数的统计诠释;算符概念;薛定谔方程 3.教学内容 第一节 波函数的统计诠释 一、波粒二象性 教学要点:掌握描述微观粒子运动状态的物理量;掌握波函数的性质,波函数的归一 化,掌握波函数的概率解释;理解动量概率分布;初步理解不确定度关系;算符本征函数 和本征值。 二、力学量的引进 教学要点:力学量平均值计算方法,力学量算符引进,掌握哈密顿算符的书写。 三、统计诠释对波函数的要求 教学要点:理解统计诠释对波函数提出的单值、有限、连续、平方可积等要求。 第二节 薛定谔方程 一、薛定谔方程的引进和讨论 教学要点:对比薛定谔方程与经典牛顿方程,掌握薛定谔方程的书写;基于薛定谔方 程掌握概率流密度矢量,理解定域概率守恒定律。 二、能量本征方程 教学要点:了解能量本征方程,掌握定态概念,了解定态与非定态随时间变化的特 点。 三、多粒子体系的薛定谔方程 教学要点:掌握多粒子体系的薛定谔方程的书写。 第三节 量子态叠加原理 一、量子态及其表象 教学要点:初步了解表象概念,了解坐标表象和动量表象及其变换方法。 二、量子态叠加原理 教学要点:了解态叠加原理;了解量子态的测量与波函数塌缩的现象。 4.教学方法 教师讲授,师生讨论,翻转课堂,指导学生自主学习等。 5.教学评价

课后相应习题,补充习题,开放课题讨论“量子力学的测量内涵,塌缩的理解”, 完成“观最强朋友圈合影,走进量子力学的黄金时代”小论文。 第二章一维势场中的粒子 1.教学目标 本章要求学生掌握一维势场中粒子能量本征态的一般性质:无限深方势阱,离散谱: 有限深方势阱:方势垒的反射与透射:方势阱的反射、透射与共振:一维谐振子系统的求 解。掌握微观体系的物理研究方法和前沿进展,熟悉物理学新发现、新理论、新技术对社 会的影响。 2.教学重难点 无限深方势与有限深方势的求解,奇偶宇称态的理解,厄密多项式,谐振子解的特点 3.教学内容 第一节一维势场中粒子能量本征态的一般性质 教学要点:掌握一维粒子能量本征态的共同特点,掌握字称概念,理解几个重要定 理。 第二节方势 一、无限深方势与有限深方势 教学要点:掌握无限深方势的求解,了解能量量子化特点:理解有限深方势阱的奇偶 字称态:束缚态和离散谱概念 二、方势垒的反射与透射 教学要点:了解方势垒的反射与透射:对比方势阱的反射、透射与共振。 第三节一维谐振子 教学要点:了解一维谐振子的求解过程,掌握厄密多项式,掌握谐振子解的特点 4.教学方法 教师讲授,同伴教学,翻转课堂,师生讨论,指导学生自主学习等。 5.教学评价 第三章力学量用算符表示 L.教学目标 本章要求学生掌握算符运算规则:厄米算符的定义和特性:量子力学的基本对易式 厄米算符的本征值和本征函数:动量和角动量算符的表达及对易关系:算符的共同本征态 球谐函数:连续谱本征函数的归一化:守恒量与对称性的关系。科学思维方法的训练,掌 握数学和物理相关的基础知识,运用物理学理论和方法解释或理解物理规律
课后相应习题,补充习题,开放课题讨论“量子力学的测量内涵,塌缩的理解”, 完成“观最强朋友圈合影,走进量子力学的黄金时代”小论文。 第二章 一维势场中的粒子 1.教学目标 本章要求学生掌握一维势场中粒子能量本征态的一般性质;无限深方势阱,离散谱; 有限深方势阱;方势垒的反射与透射;方势阱的反射、透射与共振;一维谐振子系统的求 解。掌握微观体系的物理研究方法和前沿进展,熟悉物理学新发现、新理论、新技术对社 会的影响。 2.教学重难点 无限深方势与有限深方势的求解,奇偶宇称态的理解,厄密多项式,谐振子解的特点 3.教学内容 第一节 一维势场中粒子能量本征态的一般性质 教学要点:掌握一维粒子能量本征态的共同特点,掌握宇称概念,理解几个重要定 理。 第二节 方势 一、无限深方势与有限深方势 教学要点:掌握无限深方势的求解,了解能量量子化特点;理解有限深方势阱的奇偶 宇称态;束缚态和离散谱概念。 二、方势垒的反射与透射 教学要点:了解方势垒的反射与透射;对比方势阱的反射、透射与共振。 第三节 一维谐振子 教学要点:了解一维谐振子的求解过程,掌握厄密多项式,掌握谐振子解的特点。 4.教学方法 教师讲授,同伴教学,翻转课堂,师生讨论,指导学生自主学习等。 5.教学评价 课后相应习题,补充习题,开放课题讨论“势垒贯穿拓展,双势垒周期性势垒问题”,实践 教学“连续波实验”。 第三章 力学量用算符表示 1.教学目标 本章要求学生掌握算符运算规则;厄米算符的定义和特性;量子力学的基本对易式; 厄米算符的本征值和本征函数;动量和角动量算符的表达及对易关系;算符的共同本征态, 球谐函数;连续谱本征函数的归一化;守恒量与对称性的关系。科学思维方法的训练,掌 握数学和物理相关的基础知识,运用物理学理论和方法解释或理解物理规律

2.教学重难点 算符概念,对易关系,量子力学本征方程的内涵,不确定度关系,共同本状态 3.教学内容 第一节算符的运算规则 教学要点:了解算符的概念和基本的运算规则:重点掌握厄米算符概念:掌握量子力 学的基本对易式。 第二节厄米算符的本征值与本征函数 教学要点:理解量子力学本征方程的内涵:掌握厄米算符本征值、本征函数的特点: 掌握几个典型系统的本征方程的求解。 第三节共同本征函数 一、不确定度关系的严格证明 教学要点:掌握不确定关系的严格证明并会应用。 二、共同本征态,球谱函数 教学要点:掌握角动量算符的对易关系,理解球谐函数的求解过程以及解的特点。 三、对易力学量完全集 教学要点:掌握力学量的完全集概念,了解几个常见量子系统的力学量对易守恒完全 集。 第四节力学量随时间的演化 教学要点:了解量子力学中力学量随时间演化的特点:掌握量子力学中守恒量的定义 和特征:理解能级简并与守恒量的关系。 4.教学方法 教师讲授,同伴教学,翻转课堂,实践教学,指导学生自主学习等 5.教学评价 课后相应习题,补充习题,开放课题讨论“能量时间不确定关系的数学本质”,创新拓展课 题“非平衡状态下所诵现的新奇物理现象”,量子实验课“拉比振荡”。 第四章中心力场 1.教学日标 本章要求学生掌握中心力场中粒子运动的一般性质:无限深球方势阱和三维各向同性 谐振子:氢原子的求解与讨论。加强科学的方法论和科学思维方法等的训练。 2.教学重难点 中心力场角动量守恒,两体问题转单体问题的研究方法,能量简并度的讨论
2.教学重难点 算符概念,对易关系,量子力学本征方程的内涵,不确定度关系,共同本状态 3.教学内容 第一节 算符的运算规则 教学要点:了解算符的概念和基本的运算规则;重点掌握厄米算符概念;掌握量子力 学的基本对易式。 第二节 厄米算符的本征值与本征函数 教学要点:理解量子力学本征方程的内涵;掌握厄米算符本征值、本征函数的特点; 掌握几个典型系统的本征方程的求解。 第三节 共同本征函数 一、不确定度关系的严格证明 教学要点:掌握不确定关系的严格证明并会应用。 二、共同本征态,球谐函数 教学要点:掌握角动量算符的对易关系,理解球谐函数的求解过程以及解的特点。 三、对易力学量完全集 教学要点:掌握力学量的完全集概念,了解几个常见量子系统的力学量对易守恒完全 集。 第四节 力学量随时间的演化 教学要点:了解量子力学中力学量随时间演化的特点;掌握量子力学中守恒量的定义 和特征;理解能级简并与守恒量的关系。 4.教学方法 教师讲授,同伴教学,翻转课堂,实践教学,指导学生自主学习等 5.教学评价 课后相应习题,补充习题,开放课题讨论“能量时间不确定关系的数学本质”,创新拓展课 题“非平衡状态下所涌现的新奇物理现象”,量子实验课“拉比振荡”。 第四章 中心力场 1.教学目标 本章要求学生掌握中心力场中粒子运动的一般性质;无限深球方势阱和三维各向同性 谐振子; 氢原子的求解与讨论。加强科学的方法论和科学思维方法等的训练。 2.教学重难点 中心力场角动量守恒,两体问题转单体问题的研究方法,能量简并度的讨论

3.教学内容 第一节中心力场中粒子运动的一般性质 一、角动量守恒与径向方程 教学要点:掌握中心力场下角动量守恒性质,掌握径向方程的导出和求解。 二、两体问题化为单体问题 教学要点:理解两体问题转单体问题的研究方法:理解质心坐标和相对坐标的引入。 掌握方程的转化。 第二节无限深球方势阱和三维各向同性谐振子 教学要点:了解无限深球方势阱能量本征值和本征函数:掌握利用分离变量法求解 维各向同(异)性谐振子本征能级和本征波函数,会进行能量简并度的讨论。 第三节氢原子 教学要点:了解氢原子的求解过程,理解能量本征态和本征函数的特点,包括能级简 并度和电子在径向、角向概率分布规律。 4.教学方法 教师讲授,师生讨论,指导学生自主学习等 5.教学评价 课后相应习题 ,补充习,思考题等开放课题讨论“力学量随时间的演化和对称性 的关系讨论”,创新拓展课题“天问一号是否可以靠电磁力加速”。 第五章量子力学矩阵表示 1.教学目标 本章要求学生掌握量子态的不同表象以及么正变换:力学量算符的矩阵表示:量子力 学的矩阵表示,包括薛定谔方程、平均值方程和本征方程的矩阵形式:了解Dirac符号的 使用。增强物理方法的训练,物理认知能力、抽象思维能力等的培养。 2.教学重难点 量子态在不同表象下的描述,表象变换,无穷维函数空间的概念,Dirac符号的书写 运 3.教学内容 第一节量子态的不同表象 一、量子态和力学量的矩阵表示 教学要点:了解一个量子态在不同表象下的描述:了解无穷维函数空间的概念,以及 在函数空间中量子态的矩阵表示
3.教学内容 第一节 中心力场中粒子运动的一般性质 一、角动量守恒与径向方程 教学要点:掌握中心力场下角动量守恒性质,掌握径向方程的导出和求解。 二、两体问题化为单体问题 教学要点:理解两体问题转单体问题的研究方法;理解质心坐标和相对坐标的引入, 掌握方程的转化。 第二节 无限深球方势阱和三维各向同性谐振子 教学要点:了解无限深球方势阱能量本征值和本征函数;掌握利用分离变量法求解三 维各向同(异)性谐振子本征能级和本征波函数,会进行能量简并度的讨论。 第三节 氢原子 教学要点:了解氢原子的求解过程,理解能量本征态和本征函数的特点,包括能级简 并度和电子在径向、角向概率分布规律。 4.教学方法 教师讲授,师生讨论,指导学生自主学习等 5.教学评价 课后相应习题,补充习题,思考题等;开放课题讨论“力学量随时间的演化和对称性 的关系讨论”,创新拓展课题“天问一号是否可以靠电磁力加速”。 第五章 量子力学矩阵表示 1.教学目标 本章要求学生掌握量子态的不同表象以及幺正变换;力学量算符的矩阵表示;量子力 学的矩阵表示,包括薛定谔方程、平均值方程和本征方程的矩阵形式;了解 Dirac 符号的 使用。增强物理方法的训练,物理认知能力、抽象思维能力等的培养。 2.教学重难点 量子态在不同表象下的描述,表象变换,无穷维函数空间的概念,Dirac 符号的书写 运算。 3.教学内容 第一节 量子态的不同表象 一、量子态和力学量的矩阵表示 教学要点:了解一个量子态在不同表象下的描述;了解无穷维函数空间的概念,以及 在函数空间中量子态的矩阵表示

二、量子力学的矩阵形式 教学要点:掌握薛定谔方程、平均值方程和本征方程的矩阵形式的导出和求解。 第二节Dirac符号 教学要点:掌握左矢右矢、对偶空间的概念:掌握Dirc符号的书写,以及基于 Dirac符号的简单运算。 4.教学方法 教师讲授,师生讨论,指导学生自主学习等。 5.教学评价 课后相应习恩,补充习题,思考题等:创新拓展课题“一维扩展指南针模型”, 第六章自旋与全同粒子 1.教学目标 本章要求学生掌握电子自旋态和自旋算符:Pauli矩阵:全同粒子体系的交换对称 性:两个全同粒子组成体系:泡利原理:N个全同粒子波函数:自旋单态和三重态:自旋 纠缠态。培养和提高学生的抽象思维能力和解决前沿交叉学科领域量子问题的能力。 2.教学重难点 电子自旋概念,全同性原理,自旋纠缠态概念 3.教学内容 第一节自旋 一、电子自旋态 教学要点:了解自旋假设的实验基础:理解电子自旋概念:掌握电子自旋态的描述, 以及旋量波函数的书写。 二、自旋算符与Pauli矩阵 教学要点:掌握Pauli矩阵及其性质。 第二节全同粒子体系 一、全同粒子体系的交换对称性 教学要点:掌握全同粒子概念,以及全同性原理:理解对称波函数和反对称波函数的 概念:掌握Fermi子和Bose子概念。 二、N个粒子组成的体系 教学要点:掌握两个全同粒子组成体系的波函数书写:掌握N个全同Fermi子和Bose 子体系的波函数的书写。 第三节自旋单态与三重态 教学要点:掌握两个电子自旋单态和三重态;了解自旋纠缠态概念
二、量子力学的矩阵形式 教学要点:掌握薛定谔方程、平均值方程和本征方程的矩阵形式的导出和求解。 第二节 Dirac 符号 教学要点:掌握左矢右矢、对偶空间的概念;掌握 Dirac 符号的书写,以及基于 Dirac 符号的简单运算。 4.教学方法 教师讲授,师生讨论,指导学生自主学习等。 5.教学评价 课后相应习题,补充习题,思考题等;创新拓展课题“一维扩展指南针模型”。 第六章 自旋与全同粒子 1.教学目标 本章要求学生掌握电子自旋态和自旋算符;Pauli 矩阵;全同粒子体系的交换对称 性;两个全同粒子组成体系;泡利原理;N 个全同粒子波函数;自旋单态和三重态;自旋 纠缠态。培养和提高学生的抽象思维能力和解决前沿交叉学科领域量子问题的能力。 2.教学重难点 电子自旋概念,全同性原理,自旋纠缠态概念 3.教学内容 第一节 自旋 一、电子自旋态 教学要点:了解自旋假设的实验基础;理解电子自旋概念;掌握电子自旋态的描述, 以及旋量波函数的书写。 二、自旋算符与 Pauli 矩阵 教学要点:掌握 Pauli 矩阵及其性质。 第二节 全同粒子体系 一、全同粒子体系的交换对称性 教学要点:掌握全同粒子概念,以及全同性原理;理解对称波函数和反对称波函数的 概念;掌握 Fermi 子和 Bose 子概念。 二、N 个粒子组成的体系 教学要点:掌握两个全同粒子组成体系的波函数书写;掌握 N 个全同 Fermi 子和 Bose 子体系的波函数的书写。 第三节 自旋单态与三重态 教学要点:掌握两个电子自旋单态和三重态;了解自旋纠缠态概念

4.教学方法 教师讲授,师生讨论,实践教学,指导学生自主学习等。 5.教学评价 课后相应习题,补充习题,思考题等:创新拓展课题“贝尔不等式的实验验证”。 第七章微扰论与量子跃迁 1.教学目标 本章要求学生掌握定态微扰理论:量子跃迁:突发微扰和绝热微扰:周期微扰,有限时 间内常微扰:能量-时间不确定度关系。培养和提高学生对非精确求解、自旋纠缠态等复杂 系统的求解能力,掌握对近似解的误差分析和数据处理等基本技能,锤炼科学思维能力和 科研创新能力。 2.教学重难点 定态微扰理论,量子跃迁 3.教学内容 第一节微扰论 教学要点:了解几种近似方法;掌握定态微扰理论,会用微扰方法处理非简并和简并 情况下的量子系统。 第二节量子跃迁 教学要点:了解量子态随时间的演化规律:了解突发微扰和绝热微扰:周期微扰,以 及有限时间内常微扰 4.教学方法 教师讲授,师生讨论,指导学生自主学习等。 5.教学评价 课后相应习题,补充习题,思考等:创新拓展课题“一维周期场电子运动的模型和 计算”。 四、学时分配 表2:各章节的具体内容和学时分配表 章节 章节内容 学时分配 第一章 波函数和薛定谔方程 14学时 第二章 维势场中的粒子 14学时
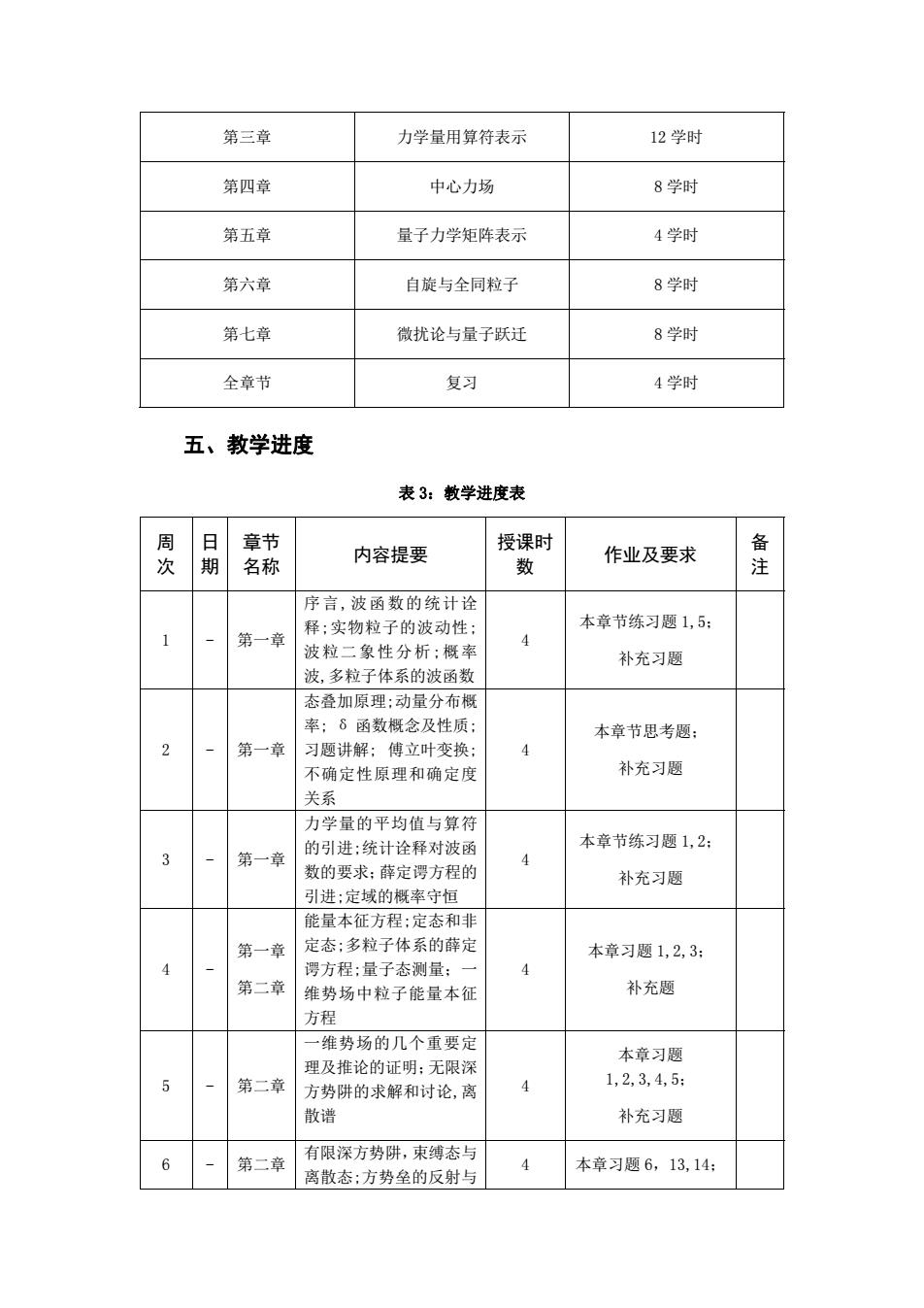
4.教学方法 教师讲授,师生讨论,实践教学,指导学生自主学习等。 5.教学评价 课后相应习题,补充习题,思考题等;创新拓展课题“贝尔不等式的实验验证”。 第七章 微扰论与量子跃迁 1.教学目标 本章要求学生掌握定态微扰理论;量子跃迁;突发微扰和绝热微扰;周期微扰,有限时 间内常微扰;能量-时间不确定度关系。培养和提高学生对非精确求解、自旋纠缠态等复杂 系统的求解能力,掌握对近似解的误差分析和数据处理等基本技能,锤炼科学思维能力和 科研创新能力。 2.教学重难点 定态微扰理论,量子跃迁 3.教学内容 第一节 微扰论 教学要点:了解几种近似方法;掌握定态微扰理论,会用微扰方法处理非简并和简并 情况下的量子系统。 第二节 量子跃迁 教学要点:了解量子态随时间的演化规律;了解突发微扰和绝热微扰;周期微扰,以 及有限时间内常微扰。 4.教学方法 教师讲授,师生讨论,指导学生自主学习等。 5.教学评价 课后相应习题,补充习题,思考题等;创新拓展课题“一维周期场电子运动的模型和 计算”。 四、学时分配 表 2:各章节的具体内容和学时分配表 章节 章节内容 学时分配 第一章 波函数和薛定谔方程 14 学时 第二章 一维势场中的粒子 14 学时
第三章 力学量用算符表示 12学时 第四章 中心力场 8学时 第五章 量子力学矩阵表示 4学时 第六章 自旋与全同粒子 8学时 第七章 微扰论与量子跃迁 8学时 全章节 复习 4学时 五、教学进度 表3:教学进度表 周日章节 内容提要 课 次期名称 数 作业及要求 注 序言波函数的统计 第一章 释 实物 子的波动性 本章节练习题1,5: 粒二象性分析:概率 补充习题 波,多粒子体系的波函数 态叠加原理:动量分布概 室:8函款概今及性质 本章节思考题: 2 第一章 习题讲解 傅立叶变换 4 不确定性原理和确定度 补充习题 关系 力学量的平均值与算符 的引进:统计诠释对波函 本章节练习题1,2: 3 第一章 数的要求:薛定方程的 4 补充习题 引进:定域的概率守恒 能量本征方程:定态和非 第一章 定态:多粒子体系的薛定 本章习题1,2,3: 四方程:量子态测量: 4 第二章 维势场中粒子能量本征 补充题 方程 一维势场的几个重要定 本竞习题 理及推论的证明:无限深 第二章 方势阱的求解和讨论,离 1,2,34,5: 补充习题 第二章 有限深方势阱,束缚态与 离散态:方势垒的反射与 本章习题6,13,14:
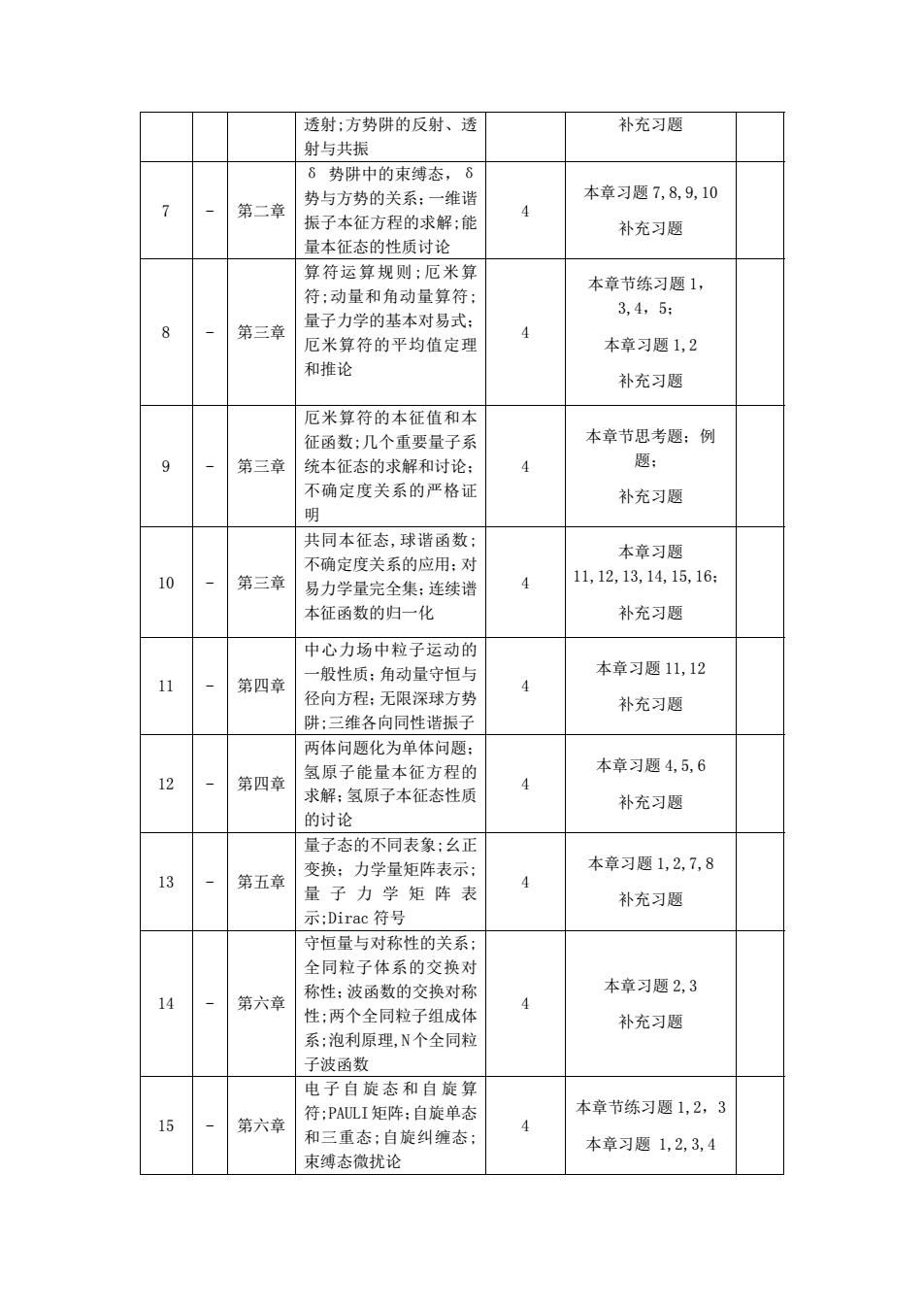
第三章 力学量用算符表示 12 学时 第四章 中心力场 8 学时 第五章 量子力学矩阵表示 4 学时 第六章 自旋与全同粒子 8 学时 第七章 微扰论与量子跃迁 8 学时 全章节 复习 4 学时 五、教学进度 表 3:教学进度表 周 次 日 期 章节 名称 内容提要 授课时 数 作业及要求 备 注 1 - 第一章 序言,波函数的统计诠 释;实物粒子的波动性; 波粒二象性分析;概率 波,多粒子体系的波函数 4 本章节练习题 1,5; 补充习题 2 - 第一章 态叠加原理;动量分布概 率; δ 函数概念及性质; 习题讲解; 傅立叶变换; 不确定性原理和确定度 关系 4 本章节思考题; 补充习题 3 - 第一章 力学量的平均值与算符 的引进;统计诠释对波函 数的要求;薛定谔方程的 引进;定域的概率守恒 4 本章节练习题 1,2; 补充习题 4 - 第一章 第二章 能量本征方程;定态和非 定态;多粒子体系的薛定 谔方程;量子态测量;一 维势场中粒子能量本征 方程 4 本章习题 1,2,3; 补充题 5 - 第二章 一维势场的几个重要定 理及推论的证明;无限深 方势阱的求解和讨论,离 散谱 4 本章习题 1,2,3,4,5; 补充习题 6 - 第二章 有限深方势阱,束缚态与 离散态;方势垒的反射与 4 本章习题 6,13,14;
透射:方势阱的反射、透 补充习题 射与共振 8势阱中的柬缚态 8 势与方势的关系: 一维话 本章习题7,8,9,10 第二章 振子本征方程的求解:能 补充习题 量本征态的性质过论 算符运算规则:厄米算 符:动量和角动量算符 本章节练习题1 3,4,5 第三章 童子力学的基本对易式; 厄米算符的平均值定理 本章习题1,2 和推论 补充习题 厄米算符的本征值和本 征函数:几个重要量子系 本章节思考题:例 9 第三章 统本征态的求解和讨论: 题: 不确定度关系的严格证 补充习题 共同本征态,球谐函数 本章习题 不确定度关系的应用:对 第三章 11,12,13,14,15,16: 易力学量完全集:连续谱 本征函数的归一化 补充习题 中心力场中粒子运动的 本章习题11,12 第四章 般性质:角动量守恒 4 径向方程:无限深球方势 补充习题 阱:三维名向同性谐振子 两体间顺化为单体间颗: 氢原子能量本征方程的 本章习题4.5.6 12 第四 求解:氢原子本征态性 4 补充习题 的讨论 量子态的不同表象:么正 变换:力学量矩阵表示 本章习题1,2,7,8 第五章 子力学矩阵表 4 补充习题 示:Dirac符号 守恒量与对称性的关系: 全同粒子体系的交换对 称性:波函影的交换对称 本章习题2,3 第六章 4 补充习题 子波函数 电子自旋态和自旋算 符:PAULI矩阵:自旋单态 本章节练习题1,2,3 15 第六章 和三重态:自旋纠缠态 4 本章习题1,2,34 束缚态微扰论
透射;方势阱的反射、透 射与共振 补充习题 7 - 第二章 δ 势阱中的束缚态,δ 势与方势的关系;一维谐 振子本征方程的求解;能 量本征态的性质讨论 4 本章习题 7,8,9,10 补充习题 8 - 第三章 算符运算规则;厄米算 符;动量和角动量算符; 量子力学的基本对易式; 厄米算符的平均值定理 和推论 4 本章节练习题 1, 3,4,5; 本章习题 1,2 补充习题 9 - 第三章 厄米算符的本征值和本 征函数;几个重要量子系 统本征态的求解和讨论; 不确定度关系的严格证 明 4 本章节思考题;例 题; 补充习题 10 - 第三章 共同本征态,球谐函数; 不确定度关系的应用;对 易力学量完全集;连续谱 本征函数的归一化 4 本章习题 11,12,13,14,15,16; 补充习题 11 - 第四章 中心力场中粒子运动的 一般性质;角动量守恒与 径向方程;无限深球方势 阱;三维各向同性谐振子 4 本章习题 11,12 补充习题 12 - 第四章 两体问题化为单体问题; 氢原子能量本征方程的 求解;氢原子本征态性质 的讨论 4 本章习题 4,5,6 补充习题 13 - 第五章 量子态的不同表象;幺正 变换;力学量矩阵表示; 量子力学矩阵表 示;Dirac 符号 4 本章习题 1,2,7,8 补充习题 14 - 第六章 守恒量与对称性的关系; 全同粒子体系的交换对 称性;波函数的交换对称 性;两个全同粒子组成体 系;泡利原理,N个全同粒 子波函数 4 本章习题 2,3 补充习题 15 - 第六章 电子自旋态和自旋算 符;PAULI矩阵;自旋单态 和三重态;自旋纠缠态; 束缚态微扰论 4 本章节练习题 1,2,3 本章习题 1,2,3,4