《数学物理方法(英文版)》课程教学大纲 一、课程基本信息 英文名称 Mathematical methods for Physicists 课程代码 PHYS3103 课程性质Required 授课对象 Physics (international) 学分 4 credits 学时 72 hours 主讲教师 Ruidong Zhu(朱睿东) 修订日期 2023.9 指定教材 Philippe Dennery and Andre Krzywicki,Mathematics for physicists,Dover Publications,INC.,Mineola,New York 二、课程目标 (一)总体目标: Mathematical method for physicists is a fundamental course for many specialties.The course aims to provide students with:complex analysis (including complex variables,analytic functions. Cauchy theorem,residues,contour integrals and Laurent series),techniques to solve differential equations (including the method of separation of variables.Legendre polynomial.spherical harmonic functions,Gren functions and Fourier transforms)and knowledge of special functions (including Bessel functions,the Gamma function,the Beta function and some basics of hypergeometric functions).The course is a prerequisite to Electrodynamics,Statistical Physics, Solid State Physics and Quantum Mechanics. (二)课程目标: i课程目标l:As the last mathematical ouse during the undergraduate study,this cours the mathematical knowledge and skill necessarily needed for studying advanced physics courses.Students are required to learn the basic knowledge for the complex analysis and some properties of the differential equations and the special functions. 课程目标2:In addition,thiscourse soopens the road to lear other advanced mathematical courses Cauchy theorem is deeply related with thehom oog时neeythe时tk。re Consequently,the course also aims to stimulate students'interest in further studying more advanced courses. 课程目标3:Many theorems in this course are deeply related to the linear algebra and that the have aredy leamed in the previous mester Therefore,the are also required to reviewsome of the imporant in advanced mathematics and linear
《数学物理方法(英文版)》课程教学大纲 一、课程基本信息 英文名称 Mathematical methods for Physicists 课程代码 PHYS3103 课程性质 Required 授课对象 Physics (international) 学 分 4 credits 学 时 72 hours 主讲教师 Ruidong Zhu (朱睿东) 修订日期 2023.9 指定教材 Philippe Dennery and Andre Krzywicki, Mathematics for physicists, Dover Publications, INC., Mineola, New York 二、课程目标 (一)总体目标: Mathematical method for physicists is a fundamental course for many specialties. The course aims to provide students with: complex analysis (including complex variables, analytic functions, Cauchy theorem, residues, contour integrals and Laurent series), techniques to solve differential equations (including the method of separation of variables, Legendre polynomial, spherical harmonic functions, Green functions and Fourier transforms) and knowledge of special functions (including Bessel functions, the Gamma function, the Beta function and some basics of hypergeometric functions). The course is a prerequisite to Electrodynamics, Statistical Physics, Solid State Physics and Quantum Mechanics. (二)课程目标: 课程目标 1:As the last mathematical course during the undergraduate study, this course provides the mathematical knowledge and skill necessarily needed for studying advanced physics courses. Students are required to learn the basic knowledge for the complex analysis and some properties of the differential equations and the special functions. 课程目标 2:In addition, this course also opens the road to learn other advanced mathematical courses. For example, the Cauchy theorem is deeply related with the homotopy theory in algebraic topology, and the analytic functions are widely used in the study of conformal field theories. Consequently, the course also aims to stimulate students’ interest in further studying more advanced courses. 课程目标 3:Many theorems in this course are deeply related to the linear algebra and calculus that the students have already learned in the previous semesters. Therefore, the students are also required to review some of the important contents in advanced mathematics and linear
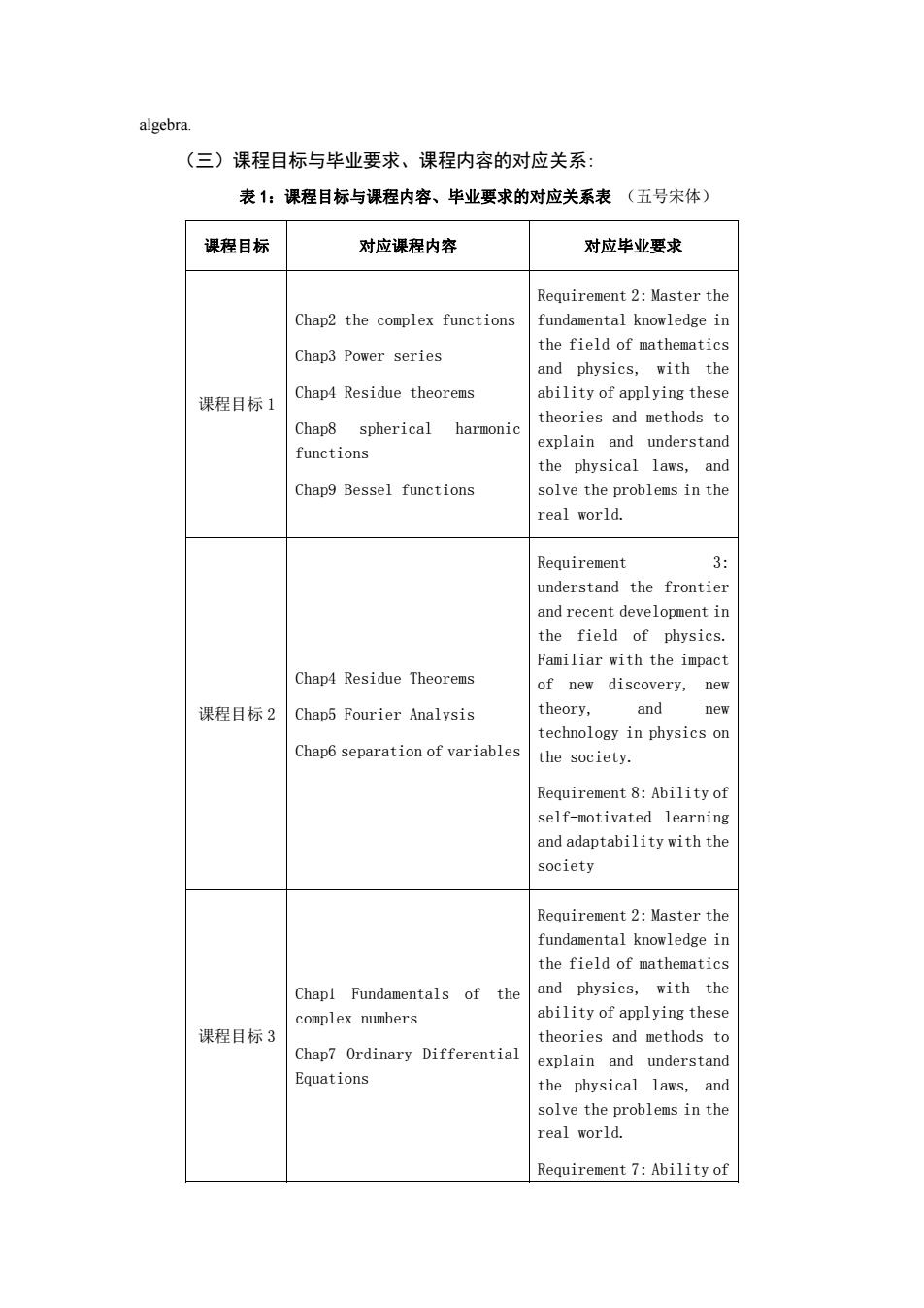
algebra (三)课程目标与毕业要求、课程内容的对应关系: 表1:课程目标与课程内容、毕业要求的对应关系表(五号宋体) 课程目标 对应课程内容 对应毕业要求 Requirement 2:Master the Chap2 the complex functions fundamental knowledge in the field of mathematics Chap3 Power series and physics,with the ability of applving these 课程目标1 Chap4 Residue theorems Chap8 spherical harmoni theories and methods explain and understand functions the physical laws,and Chap9 Bessel functions solve the problems in the ceal world. Requirement 3: understand the frontier and recent development in the field of physics. Familiar with the impact Chap4 Residue Theorems of new discovery,new 课程目标2Chap5 Fourier Analysis theory, and new technology in physics on Chap6 separation of variables the society. Requirement 8:Ability of self-motivated learnin and adaptability with the society Requirement 2:Master the fundamental knowledge in the field of mathematics Chapl Fundamentals of th and physics,with the complex numbers ability of applying these 课程目标3 theories and methods to Chap7 Ordinary Differentia xplain and understan Equations the physical laws,an solve the problems in the real world. Requirement 7:Ability of
algebra. (三)课程目标与毕业要求、课程内容的对应关系: 表 1:课程目标与课程内容、毕业要求的对应关系表 (五号宋体) 课程目标 对应课程内容 对应毕业要求 课程目标 1 Chap2 the complex functions Chap3 Power series Chap4 Residue theorems Chap8 spherical harmonic functions Chap9 Bessel functions Requirement 2: Master the fundamental knowledge in the field of mathematics and physics, with the ability of applying these theories and methods to explain and understand the physical laws, and solve the problems in the real world. 课程目标 2 Chap4 Residue Theorems Chap5 Fourier Analysis Chap6 separation of variables Requirement 3: understand the frontier and recent development in the field of physics. Familiar with the impact of new discovery, new theory, and new technology in physics on the society. Requirement 8: Ability of self-motivated learning and adaptability with the society 课程目标 3 Chap1 Fundamentals of the complex numbers Chap7 Ordinary Differential Equations Requirement 2: Master the fundamental knowledge in the field of mathematics and physics, with the ability of applying these theories and methods to explain and understand the physical laws, and solve the problems in the real world. Requirement 7: Ability of

investigating.designing projects. processin data during research,and academic communication. 三、教学内容 第-章Fundamentals of Complex Variables 1.教学目标 This chapter requires the students to understand the basic operations of complex numbers,different representations of a complex number,Euler's formula.The students are expected to expand their knowledge from the real numbers to complex numbers,understand the principles of the materialist dialectics,and construct a scientific understanding of the world. 2.教学难点 Representations of the complex numbers and the applications of Euler's formula. 3.教学内容 A.Algebraic operation Master the addition,subtraction,multiplication,division between two complex numbers,as well as the conjugation,inverse of a single complex number. B.Representations of a complex number Complex plane,rectangular and polar coordinates. C.Euler's formula,the calculation of exponential of a complex number the geometric meaning of the modulus and argument of a complex number. 4.教学方法 Lectures,discussions,etc 5.教学评价 Corresponding exercises and quiz. 第二章The complex function 1.教学目标 The students are required to understand the definition of a complex function, an analytic function and the multi-valuedness of some complex functions,the branch cut,the differential and integrals of a complex functions,the similarity and
investigating, designing projects, processing data during research, and academic communication. 三、教学内容 第一章 Fundamentals of Complex Variables 1. 教学目标 This chapter requires the students to understand the basic operations of complex numbers, different representations of a complex number, Euler’s formula. The students are expected to expand their knowledge from the real numbers to complex numbers, understand the principles of the materialist dialectics, and construct a scientific understanding of the world. 2. 教学难点 Representations of the complex numbers and the applications of Euler’s formula. 3. 教学内容 A. Algebraic operation Master the addition, subtraction, multiplication, division between two complex numbers, as well as the conjugation, inverse of a single complex number. B. Representations of a complex number Complex plane, rectangular and polar coordinates. C. Euler’s formula, the calculation of exponential of a complex number, the geometric meaning of the modulus and argument of a complex number. 4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 第二章 The complex function 1. 教学目标 The students are required to understand the definition of a complex function, an analytic function and the multi-valuedness of some complex functions, the branch cut, the differential and integrals of a complex functions, the similarity and

difference between real analysis and the complex analysis,the dependence of integral on the path. 2.教学难点 Multi-valuedness of a complex function and the associated branch cut,the path dependence of a complex integral. 3.教学内容 A.definition of a complex function:map from complex number to the complex number:definition of an analytic function. B.Mutli-valuedness of some complex functions,and the introduction of the branch cut. C.continuity and differentiability of a complex function,Cauchy-Riemann condition,and the analytical function D.Integrals of a complex function and its path dependent 4.教学方法 Lectures,discussions,ete 5.教学评价 Corresponding exercises and quiz. 第三章Power Series 1.教学目标 Understand the convergence of a series.and apply several methods to check the 2.教学难点 Convergence vs uniform convergence,Laurent expansion 3.教学内容 A.definition of convergence and uniform convergence. B.the general method to check the convergence of a series C.various methods to obtain the Laurent expansion 4.教学方法 Lectures,discussions,etc 5.教学评价
difference between real analysis and the complex analysis, the dependence of integral on the path. 2. 教学难点 Multi-valuedness of a complex function and the associated branch cut, the path dependence of a complex integral. 3. 教学内容 A. definition of a complex function: map from complex number to the complex number; definition of an analytic function. B. Mutli-valuedness of some complex functions, and the introduction of the branch cut. C. continuity and differentiability of a complex function, Cauchy-Riemann condition, and the analytical function D. Integrals of a complex function and its path dependent 4. 教学方法 Lectures, discussions, etc. 5. 教学评价 Corresponding exercises and quiz. 第三章 Power Series 1. 教学目标 Understand the convergence of a series, and apply several methods to check the convergence. Uniform convergence, convergence circle, local expansion of an analytical function, Taylor and Laurent series 2. 教学难点 Convergence vs uniform convergence, Laurent expansion 3. 教学内容 A. definition of convergence and uniform convergence. B. the general method to check the convergence of a series C. various methods to obtain the Laurent expansion 4.教学方法 Lectures, discussions, etc. 5.教学评价

Corresponding exercises and quiz. 第四章Residue Theorem 1.教学日目标 Master the calculation of the residue of an analytical function at the pole understand the general proof of the residue theorem,and get familiar with different techniques to apply the residue theorem to calculate the integrals. 2.教学难点 The concept of residue and its calculations,residue theorem and its application to the calculation of various integrals. 3.教学内容 A.the definition of the residue based on the laurent expansion. B.the proof of the residue theorem based on the Cauchy integral theorem. C.Various techniques to calculate the residue,especially at the rank 1 pole. D.the application of the residue theorem to the calculation of the integrals. 1.the integrals of trigonometric function 2.the integrals over the whole real axis 3.the appropriate choice of the closed contours E.Principle integral 4.教学方法 Lectures,discussions,etc. 5.教学评价 Corresponding exercises and quiz. 第五章Laplace Transform and Fourier Analysis 1.教学目标 Master the Laplace transform,the Fourier series of a periodic function,the derivation of Fourier integrals,and the inverse Fourier transformation. 2.教学难点
Corresponding exercises and quiz. 第四章 Residue Theorem 1. 教学目标 Master the calculation of the residue of an analytical function at the pole, understand the general proof of the residue theorem, and get familiar with different techniques to apply the residue theorem to calculate the integrals. 2. 教学难点 The concept of residue and its calculations, residue theorem and its application to the calculation of various integrals. 3. 教学内容 A. the definition of the residue based on the Laurent expansion. B. the proof of the residue theorem based on the Cauchy integral theorem. C. Various techniques to calculate the residue, especially at the rank 1 pole. D. the application of the residue theorem to the calculation of the integrals. 1. the integrals of trigonometric function 2. the integrals over the whole real axis 3. the appropriate choice of the closed contours E. Principle integral 4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 第五章 Laplace Transform and Fourier Analysis 1. 教学目标 Master the Laplace transform, the Fourier series of a periodic function, the derivation of Fourier integrals, and the inverse Fourier transformation. 2. 教学难点

The idea behind the Laplace transform,the Fourier series and transformation, i.e.the transformation between space/time and momentum/frequency.The parity and the Fourier integrals after the original function is translated in space/time 3.教学内容 A.The definition of Laplace transform. B.The definition of Fourier series of a periodic function. C.Discuss the convergence of the Fourier series and its behavior at the discontinuity. D.The derivation of Fourier transformation of an a periodic function. E.several simple conclusions based on the definition of Fourier analysis 4.教学方法 Lectures,discussions,etc. 5.教学评价 Corresponding exercises and quiz. 第六章Separation of Variables 1.教学目标 Obtain the ability of transforming a physical problem into a mathematical equation,get familiar with the classification of the partial differential equation, understand the general rule for the separation of variables,and the Laplace equation under different coordinate systems 2.教学难点 Oscillation equation,Laplace equation in polar and spherical coordinate systems,and the method of separation of variables. 3.教学内容 A.Introduce the physical model for longitudinal and transverse oscillations, and derive the mathematical partial differential equations. B.Use the oscillation equation as an example to introduce the separation of variables and decompose the PDE into several ODEs C.Derive the Laplace operators in the polar and spherical coordinate systems and apply the separation of variables to transform the Laplace equations into the ODEs
The idea behind the Laplace transform, the Fourier series and transformation, i.e. the transformation between space/time and momentum/frequency. The parity symmetry, and the Fourier integrals after the original function is translated in space/time. 3. 教学内容 A. The definition of Laplace transform. B. The definition of Fourier series of a periodic function. C. Discuss the convergence of the Fourier series and its behavior at the discontinuity. D. The derivation of Fourier transformation of an a periodic function. E. several simple conclusions based on the definition of Fourier analysis 4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 第六章 Separation of Variables 1. 教学目标 Obtain the ability of transforming a physical problem into a mathematical equation, get familiar with the classification of the partial differential equation, understand the general rule for the separation of variables, and the Laplace equation under different coordinate systems 2. 教学难点 Oscillation equation, Laplace equation in polar and spherical coordinate systems, and the method of separation of variables. 3. 教学内容 A. Introduce the physical model for longitudinal and transverse oscillations, and derive the mathematical partial differential equations. B. Use the oscillation equation as an example to introduce the separation of variables and decompose the PDE into several ODEs. C. Derive the Laplace operators in the polar and spherical coordinate systems, and apply the separation of variables to transform the Laplace equations into the ODEs

4.教学方法 Lectures,discussions,etc 5.教学评价 Corresponding exercises and quiz. 第七章0 rdinary Differential Equation 1.教学目标 Introduce the general theorem for the differential equation.The eigen-functions form a complete and orthogonal basis of the functional space,and the classification as well as the series method to solve the ODE. 2.教学难点 Series method and eigen-functions 3.教学内容 A.classification of the ordinary differential equations B.the series method to obtain the solutions of ODE C.eigenfunctions and eigenvalues,relationship with the linear space 4.教学方法 Lectures,discussions,etc. 5.教学评价 Corresponding exercises and quiz. 第八章Spherical Harmonic Functions 1.教学目标 Use the series method to obtain the solution of Laplace equation in the spherical coordinate system.Derive the recursion relations for the spherical harmonic functions and Legendre functions. 2.教学难点 Property of the spherical harmonic functions. 3.教学内容
4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 第七章 Ordinary Differential Equation 1. 教学目标 Introduce the general theorem for the differential equation. The eigen-functions form a complete and orthogonal basis of the functional space, and the classification as well as the series method to solve the ODE. 2. 教学难点 Series method and eigen-functions. 3. 教学内容 A. classification of the ordinary differential equations B. the series method to obtain the solutions of ODE C. eigenfunctions and eigenvalues, relationship with the linear space. 4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 第八章 Spherical Harmonic Functions 1. 教学目标 Use the series method to obtain the solution of Laplace equation in the spherical coordinate system. Derive the recursion relations for the spherical harmonic functions and Legendre functions. 2. 教学难点 Property of the spherical harmonic functions. 3. 教学内容

A.series method to solve the Laplace equations in the spherical harmonic functions,and the asymptotic behavior of the solutions B.the recursion relation of the Legendre functions C.the characteristic functions for the Legendre functions. 4.教学方法 Lectures,discussions,etc 5.教学评价 Corresponding exercises and quiz. 第九章Bessel Functions 1.教学目标 Use the series method to obtain the solution of Laplace equation in the polar coordinate system.Derive the recursion relations for the Bessel functions 2.教学难点 Property of the Bessel functions. 3.教学内容 A.series method to solve the Laplace equations in the polar coordinate system. and the asymptotic behavior of the solutions B.the recursion relations of the Bessel functions C.the characteristic functions for the Bessel functions 4.教学方法 Lectures,discussions,etc. 5.教学评价 Corresponding exercises and quiz 四、学时分配 表2:各章节的具体内容和学时分配表 章节 章节内容 学时分配
A. series method to solve the Laplace equations in the spherical harmonic functions, and the asymptotic behavior of the solutions B. the recursion relation of the Legendre functions C. the characteristic functions for the Legendre functions. 4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 第九章 Bessel Functions 1. 教学目标 Use the series method to obtain the solution of Laplace equation in the polar coordinate system. Derive the recursion relations for the Bessel functions. 2. 教学难点 Property of the Bessel functions. 3. 教学内容 A. series method to solve the Laplace equations in the polar coordinate system, and the asymptotic behavior of the solutions B. the recursion relations of the Bessel functions C. the characteristic functions for the Bessel functions. 4.教学方法 Lectures, discussions, etc. 5.教学评价 Corresponding exercises and quiz. 四、学时分配 表 2:各章节的具体内容和学时分配表 章节 章节内容 学时分配

第一章 Fundamental of complex variables 第二章 Complex functions 8 第三章 Power series 8 第四章 Residue theorem 16 第五章 Fourier analysis 6 第六章 Separation of variables 6 第七章 Ordinary differential equation 第八章 Spherical harmonic function 8 第九章 Bessel function 8 五、教学进度 表3:教学进度表 周次 章节 名称 内容提要 授课 时数 作业及要求 备注 fundamentals of 1 the complex number,magnitud 4 Exercise 1,5; and argument Continuity and differentiability complex 4 functions Riemann theorem 4 Probleml,2: and its proof 3 Taylor expansion Problem 1,2,3: aurent expansion 4 Problem 4,5:
第一章 Fundamental of complex variables 4 第二章 Complex functions 8 第三章 Power series 8 第四章 Residue theorem 16 第五章 Fourier analysis 6 第六章 Separation of variables 6 第七章 Ordinary differential equation 8 第八章 Spherical harmonic function 8 第九章 Bessel function 8 五、教学进度 表 3:教学进度表 周次 章节 名称 内容提要 授课 时数 作业及要求 备注 1 1 fundamentals of the complex number, magnitude and argument 4 Exercise 1,5; 2 2 Continuity and differentiability of the complex functions 4 3 2 Riemann theorem and its proof 4 Problem1,2; 4 3 Taylor expansion 4 Problem 1,2,3; 5 3 Laurent expansion 4 Problem 4,5;

Classification of the singularity d definition o 4 Problem 6,13,14; poles Definition of residue based on the 4 Laurent Prob1e7,8.9,10 expansion Various techniques to calculate the and the 8 Prob1em11,12,15,16 residue theorem to the integrals Fourier series and 9 5 the derivation of 4 the Fourier integrals Several theorems of the Fourier 10 5,6 introduction 0 4 Prob1em11,12,13,14,15,16 the partia. differential equations Use separation of 11 6 4 Problem 11,12 transform into several ODEs Classification of 2order ODEs 12 based on the 4 Problem 4.5,6 singularity properties Series method to solve ODEs.the 13 4 independent Problem 1,2,7,8 solutions The Laplace operator in the 4 spberical 4 Problem 2,3 coordinate system, and
6 4 Classification of the singularity and definition of poles 4 Problem 6,13,14; 7 4 Definition of residue based on the Laurent expansion 4 Problem 7,8,9,10 8 4 Various techniques to calculate the residues and the application of the residue theorem to the integrals 8 Problem 11,12,15,16 9 5 Fourier series and the derivation of the Fourier integrals 4 10 5,6 Several theorems of the Fourier analysis, introduction on the partial differential equations 4 Problem11,12,13,14,15,16; 11 6 Use separation of variables to transform PDE into several ODEs 4 Problem 11,12 12 7 Classification of 2 nd order ODEs based on the singularity properties 4 Problem 4,5,6 13 7 Series method to solve ODEs, the two independent solutions 4 Problem 1,2,7,8 14 8 The Laplace operator in the spherical coordinate system, and 4 Problem 2,3