
物理实验中心 简谐振动参量的传感 器测量
简谐振动参量的传感 器测量

■随着科学技术的发展,测量方法也不断进步,70年代初,光 电技术迅速发展,光敏传感器计时技术在工业和家用电器中 得到大量应用。90年代初,集成霍尔传感器技术得到了迅猛 发展。各种性能的集成霍尔传感器不断涌现,在工业、交通、 通信等领域的自动控制中得到广泛的应用。 本实验将学习集成开关型霍尔传感器的特性,并用该传感器 测量弹簧振子的振动周期。集成开关型霍尔传感器测量周期 的优点是装置体积小,可靠性强,价格低廉,特别是它隔着 介质(非磁介质)仍能工作,这些是光电传感器很难做得到 的,因而有广泛的应用前景
▪ 随着科学技术的发展,测量方法也不断进步,70年代初,光 电技术迅速发展,光敏传感器计时技术在工业和家用电器中 得到大量应用。90年代初,集成霍尔传感器技术得到了迅猛 发展。各种性能的集成霍尔传感器不断涌现,在工业、交通、 通信等领域的自动控制中得到广泛的应用。 ▪ 本实验将学习集成开关型霍尔传感器的特性,并用该传感器 测量弹簧振子的振动周期。集成开关型霍尔传感器测量周期 的优点是装置体积小,可靠性强,价格低廉,特别是它隔着 介质(非磁介质)仍能工作,这些是光电传感器很难做得到 的,因而有广泛的应用前景

实验目的 ·通过测量弹簧振子振动周期,掌握霍尔传感器的特 性。了解其在自动测量和自动控制中的应用。 ·测量弹簧的倔强系数,研究弹簧振子运动规律。 ·测量集成开关型霍尔传感器的特性,掌握集成霍尔 传感器的使用方法。 用集成开关型霍尔传感器设计测量角度、转速、产 品计数、液位控制等有关应用性实验
实验目的 ▪ 通过测量弹簧振子振动周期,掌握霍尔传感器的特 性。了解其在自动测量和自动控制中的应用。 ▪ 测量弹簧的倔强系数,研究弹簧振子运动规律。 ▪ 测量集成开关型霍尔传感器的特性,掌握集成霍尔 传感器的使用方法。 ▪ 用集成开关型霍尔传感器设计测量角度、转速、产 品计数、液位控制等有关应用性实验

实验原理 1.位移法测弹簧倔强系数 ·弹簧在外力作用下将产生形变(即伸长或缩短)。在弹性限 度内,外力F和它的变形量成正比,即: F=K△Y或mg=K△Y 即胡克定律,比例系数K称为弹簧的倔强系数,其值与弹簧 的形状,材料有关。若改变施加在弹簧上的外力,并测量相 应的形变量,即可通过该式推算该弹簧的倔强系数K
实验原理 1. 位移法测弹簧倔强系数 ▪ 弹簧在外力作用下将产生形变(即伸长或缩短)。在弹性限 度内,外力F和它的变形量成正比,即: ▪ 即胡克定律,比例系数K称为弹簧的倔强系数,其值与弹簧 的形状,材料有关。若改变施加在弹簧上的外力,并测量相 应的形变量,即可通过该式推算该弹簧的倔强系数K。 F = KY或mg = KY

2.周期法测弹簧倔强系数 ·质量为M的物体系于一轻弹簧的自由端,并放置在光滑的水 平台面上,弹簧的另一端固定,这就构成一个弹簧振子。弹 簧振子将在平衡点附近来回作简谐振动,其周期为: T=2πK M 实际上弹簧本身具有质量M,它必对周期产生影响,可修 正为 T=2π1 M+PM或K=4T(M+PM,) K T2 式中P是一个介于0与1之间的系数(0<P<1),其准确值可以通过实验予 以确定,对柱形弹簧P≈13。PM称为弹簧的有效质量(亦称折合质量)
2. 周期法测弹簧倔强系数 ▪ 质量为M的物体系于一轻弹簧的自由端,并放置在光滑的水 平台面上,弹簧的另一端固定,这就构成一个弹簧振子。弹 簧振子将在平衡点附近来回作简谐振动,其周期为: ▪ 实际上弹簧本身具有质量M0,它必对周期产生影响,可修 正为 K M T = 2 2 0 2 0 4 2 T M PM K K M PM T ( ) 或 + = + = ▪ 式中P是一个介于0与1之间的系数(0<P<1),其准确值可以通过实验予 以确定,对柱形弹簧P1/3。PM0称为弹簧的有效质量(亦称折合质量)
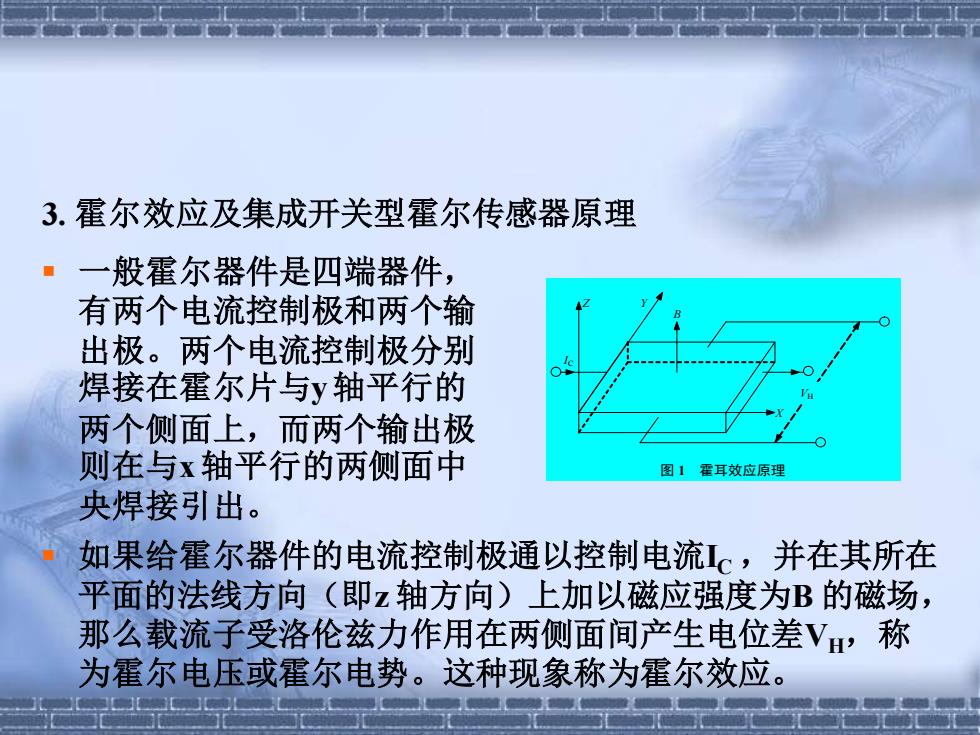
3.霍尔效应及集成开关型霍尔传感器原理 ·一般霍尔器件是四端器件, 有两个电流控制极和两个输 出极。两个电流控制极分别 焊接在霍尔片与y轴平行的 两个侧面上,而两个输出极 则在与x轴平行的两侧面中 图1霍耳效应原理 央焊接引出。 如果给霍尔器件的电流控制极通以控制电流。,并在其所在 平面的法线方向(即z轴方向)上加以磁应强度为B的磁场, 那么载流子受洛伦兹力作用在两侧面间产生电位差V,称 为霍尔电压或霍尔电势。这种现象称为霍尔效应
3. 霍尔效应及集成开关型霍尔传感器原理 图 1 霍耳效应原理 B Z Y X IC VH ▪ 一般霍尔器件是四端器件, 有两个电流控制极和两个输 出极。两个电流控制极分别 焊接在霍尔片与y 轴平行的 两个侧面上,而两个输出极 则在与x 轴平行的两侧面中 央焊接引出。 ▪ 如果给霍尔器件的电流控制极通以控制电流IC ,并在其所在 平面的法线方向(即z 轴方向)上加以磁应强度为B 的磁场, 那么载流子受洛伦兹力作用在两侧面间产生电位差VH,称 为霍尔电压或霍尔电势。这种现象称为霍尔效应

开关型霍尔传感器(集成霍尔开关)是把霍尔片产生的霍尔电压V:放大 后驱动触发电路,输出电压是能反映B的变化的方脉冲。集成霍尔开关 由稳压器、霍尔电势发生器(即硅霍尔片)、差分放大器、施密特触发 器和0C门输出五个基本部分组成。在输入端(1、2之间)输入电压Vc, 经稳压器稳压后加在霍尔发生器的两电流端。根据霍尔效应原理,当霍 尔片处于磁场中时,霍尔发生器的两电压端将会有一个霍尔电势差V 输出。VH经放大器放大以后送至施密特触发器整形,使其成为方波输 送到OC门输出。 输出 工作点 9 (ON) 释放点 (OFF) 施密特触爱器 B/mT 20 图2开关型霍尔传感器原理和输出特性
▪ 开关型霍尔传感器(集成霍尔开关)是把霍尔片产生的霍尔电压VH放大 后驱动触发电路,输出电压是能反映B的变化的方脉冲。集成霍尔开关 由稳压器、霍尔电势发生器(即硅霍尔片)、差分放大器、施密特触发 器和OC门输出五个基本部分组成。在输入端(1、2之间)输入电压Vcc, 经稳压器稳压后加在霍尔发生器的两电流端。根据霍尔效应原理,当霍 尔片处于磁场中时,霍尔发生器的两电压端将会有一个霍尔电势差VH 输出。VH 经放大器放大以后送至施密特触发器整形,使其成为方波输 送到OC门输出。 稳 压 霍 尔 片 Vcc 输出 1 3 + - 施密特触发器 2 2 图 2 开关型霍尔传感器原理和输出特性 V0/V 12 9 6 3 B/mT 0 5 10 15 20 释放点 (OFF) 工作点 (ON)

■ 当外磁场B达到“工作点”B。m时,触发器输出高电平(相对 于地电位),三极管导通,此时,OC门输出端输出低电平, 通常称这种状态为“开”;当外磁场B达到“释放点”B时, 触发器输出低电平,三极管截止,0OC门输出高电平,这时 称其为“关”状态。本实验就是利用磁钢与霍尔传感器之间 的距离周期性改变来测量弹簧的振动周期的,把这些开关信 号(方脉冲)送入计数器计数就能测出振动的周期数。 Bop与Bm是有一定差值的,此差值BH-BOp-BrD7称为霍尔开关 的磁滞。B的变化不超过B,霍尔开关不翻转,这就使得开 关输出稳定可靠。集成霍尔开关传感器的输出特性如图(2)
▪ 当外磁场B达到“工作点”Bop时,触发器输出高电平(相对 于地电位),三极管导通,此时,OC门输出端输出低电平, 通常称这种状态为“开”;当外磁场B达到“释放点”Brp时, 触发器输出低电平,三极管截止,OC门输出高电平,这时 称其为“关”状态。本实验就是利用磁钢与霍尔传感器之间 的距离周期性改变来测量弹簧的振动周期的,把这些开关信 号(方脉冲)送入计数器计数就能测出振动的周期数。 ▪ Bop与Brp是有一定差值的,此差值BH=Bop-Brp称为霍尔开关 的磁滞。B的变化不超过BH,霍尔开关不翻转,这就使得开 关输出稳定可靠。集成霍尔开关传感器的输出特性如图(2)

实验内容 1.用位移法测定弹簧倔强系数K。 实验装置如图所示。游标卡尺3固定在 支架上,在游标卡尺的活动爪上装有一 面小反射镜1,镜上有一条刻度线。利 用1的帮助(主要是为了消除视差)可 以用游标卡尺准确读出砝码托盘2末端 的位置。在砝码盘中放置质量为M的砝 码,则M产生的作用力F=Mg。设在放 置M前砝码托盘末端的位置读数为Yo, 放置后为Y,利用1)式可得: Mg=k(Y-Yo) 式中g为重力加速度
实验内容 1. 用位移法测定弹簧倔强系数 K 。 ▪ 实验装置如图所示。游标卡尺 3固定在 支架上,在游标卡尺的活动爪上装有一 面小反射镜 1,镜上有一条刻度线。利 用 1的帮助(主要是为了消除视差)可 以用游标卡尺准确读出砝码托盘 2末端 的位置。在砝码盘中放置质量为 M的砝 码,则 M产生的作用力F=Mg。设在放 置 M前砝码托盘末端的位置读数为 Y 0 , 放置后为 Y,利用(1)式可得: Mg=k(Y-Y0) 式中 g为重力加速度。 3 21

()调节支架的底脚螺丝,使焦利秤立柱垂直。 (2)将弹簧固定在焦利秤上部悬臂上。旋转悬臂,使挂于弹簧 下方的砝码盘的尖针靠拢游标尺上的小镜。 (3)法码盘中放置一定质量的砝码后,弹簧伸长。调节游标尺 的活动爪,使砝码托盘末端的针尖对准小镜上的刻线,记录 M及游标尺上相应的读数Y。 (④改变M,测量不同的M对应的Y(参看数据记录表,加砝码 过程测一次为Y1;减砝码过程再测一次为Y2,取平均)。 5)作M-Y图,验证M-Y的线性关系,并求曲线的斜率k, k=kg即为弹簧的倔强系数。 (6同时用逐差法求K和△K,并与作图法的计算结果比较
(1) 调节支架的底脚螺丝,使焦利秤立柱垂直。 (2) 将弹簧固定在焦利秤上部悬臂上。旋转悬臂,使挂于弹簧 下方的砝码盘的尖针靠拢游标尺上的小镜。 (3) 法码盘中放置一定质量的砝码后,弹簧伸长。调节游标尺 的活动爪,使砝码托盘末端的针尖对准小镜上的刻线,记录 M及游标尺上相应的读数Y。 (4) 改变M,测量不同的M对应的Y(参看数据记录表,加砝码 过程测一次为Y1;减砝码过程再测一次为Y2,取平均)。 (5) 作M-Y图,验证M-Y的线性关系,并求曲线的斜率k, k=k·g即为弹簧的倔强系数。 (6) 同时用逐差法求K和K,并与作图法的计算结果比较