
第十一章非线性回归概述曲线回归的线性化多项式回归曲线配合的拟合度
第十一章 非线性回归 ⚫概述 ⚫曲线回归的线性化 ⚫多项式回归 ⚫曲线配合的拟合度
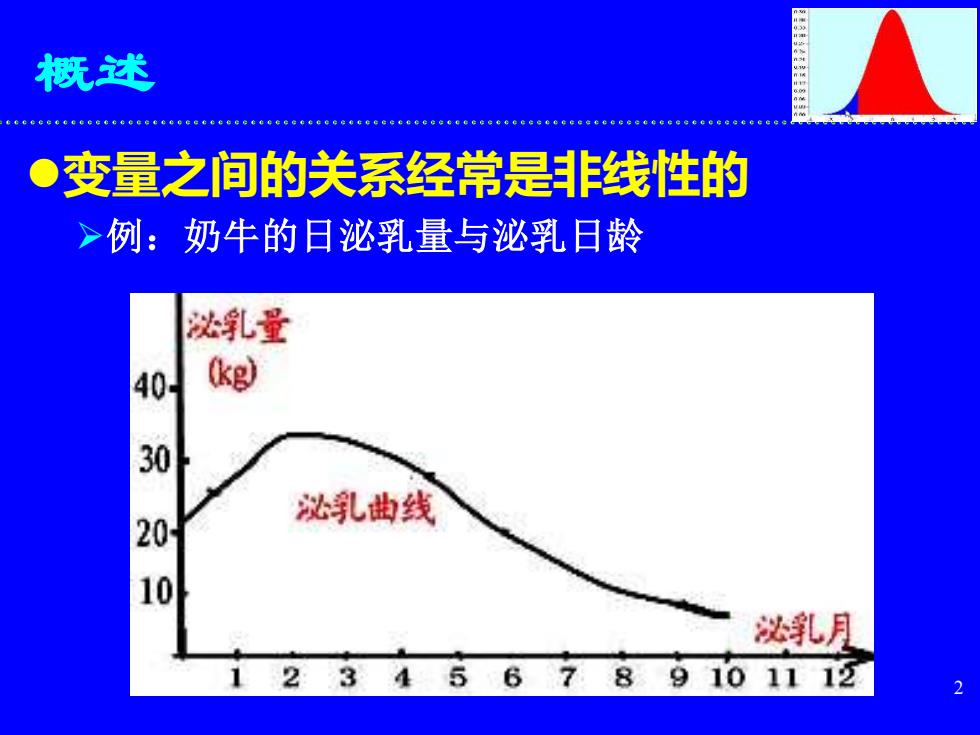
概述·变量之间的关系经常是非线性的>例:奶牛的日泌乳量与泌乳日龄泌乳量(kg)40-30泌乳曲线2010泌乳月9101112
2 概述 ⚫变量之间的关系经常是非线性的 ➢例:奶牛的日泌乳量与泌乳日龄

EARAATPEESES概述非线性回归分析>已知曲线类型·判断:根据专业知识(理论和经验),或样本数据的散点分布趋势·分析方法:曲线方程线性化直接配合曲线方程>未知曲线类型·分析方法:多项式回归
3 概述 ⚫非线性回归分析 ➢已知曲线类型 • 判断:根据专业知识(理论和经验),或样本数 据的散点分布趋势 • 分析方法:曲线方程线性化 直接配合曲线方程 ➢未知曲线类型 • 分析方法:多项式回归

TS曲线回归的线性化设有回归模型相乘Y =αX线性化:InY = lnα + β lnX+ lnee' ~ N(0,α2)Y'=α'+βX'+e一元线性回归模型相加但是2Y =αX通常的做法:不考虑误差的出现形式,只考虑模型的主体部分
4 曲线回归的线性化 ⚫设有回归模型 Y X e = 线性化: Y = X + e 但是 ? 相乘 相加 通常的做法:不考虑误差的出现形式,只考虑模 型的主体部分 一元线性回归模型
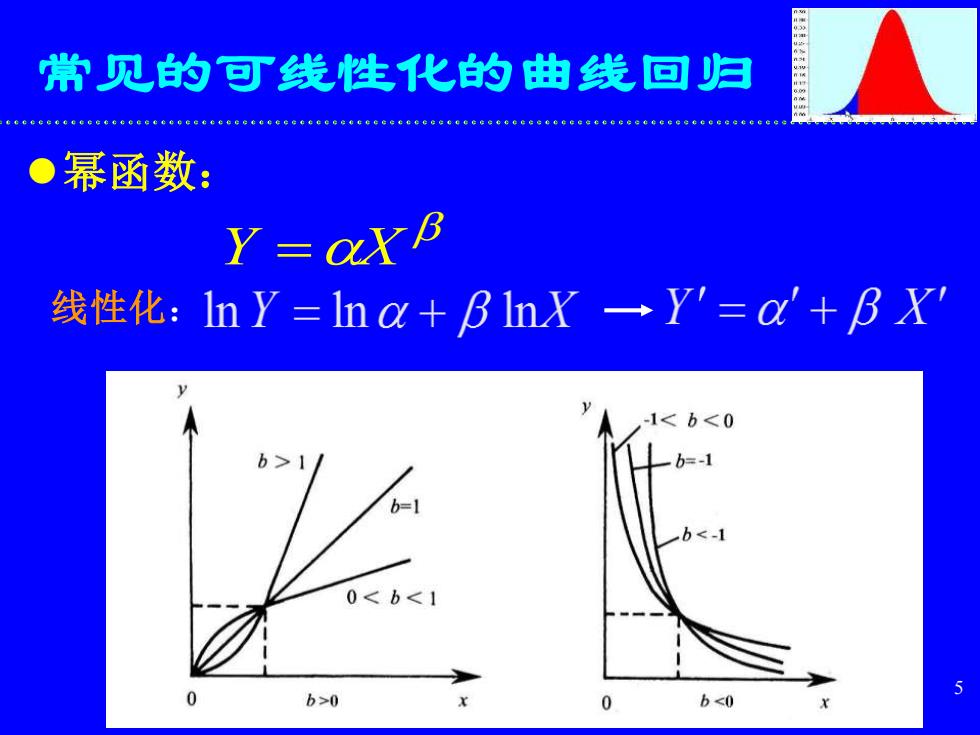
常见的可线性化的曲典线回归幂函数:Y=αXβ线性化:ln Y=lnα+βlnX —→Y'=α'+βX"b00b<0X
5 常见的可线性化的曲线回归 ⚫幂函数: Y =X 线性化:

ARASE常见的可线性化的曲典线回归●指数函数Y=αeβX线性化:一Y=α'+βXlnY = lnα+ βX(b0)00X6
6 常见的可线性化的曲线回归 ⚫指数函数 X Y e = 线性化:

OS常见的可线性化的曲线回归●对数函数Y=α+βlnXY=α+βX'线性化:b000
7 常见的可线性化的曲线回归 ⚫对数函数 Y = + ln X 线性化:

S常见的可线性化的曲线回归双曲线函数α+βY'=α+βX线性化:a>ob001
8 常见的可线性化的曲线回归 ⚫双曲线函数 Y X 1 1 = + 线性化:

S常见的可线性化的曲线回归S型曲线Y=-α+βe=α+βe-X线性化:Y'=α+βXx0
9 常见的可线性化的曲线回归 ⚫ S型曲线 X e Y − + = 1 线性化:

O41S多项式回归eeeeceeeeeeeeeeeeeeeeeeeeecee用于无法确定曲线类型的曲线回归原理:任何函数都可以用多项式来近似y= f(x)~a+bjx+b,x+11y=a+bx+bx(二项式)二次抛物线:(三项式) :y=a+bx+b,x~ +bax三次抛物线10
10 多项式回归 ⚫用于无法确定曲线类型的曲线回归 ⚫原理:任何函数都可以用多项式来近似 k k y = f x a + b x + b x ++ b x 2 1 2 ( ) 二次抛物线(二项式): 2 1 2 y = a + b x + b x 三次抛物线(三项式): 3 3 2 1 2 y = a + b x + b x + b x