
第9章简单相关与回归从数学的角度表示事物之间的联系,或者称为变量间的关系:(1)确定的函数关系,变量之间是一一对应的,可以用公式来表示。2如:圆面积与半径的关系S = r=vt距离与速度的关系S等等
第9章 简单相关与回归 从数学的角度表示事物之间的联系,或者称为变量间 的关系: (1)确定的函数关系,变量之间是一一对应的,可以用公 式来表示。 如:圆面积与半径的关系 距离与速度的关系 等等 2 S = r s = vt

(2)非确定的关系,不是一一对应的函数关系,不能用公式来表示。如:仔猪断奶重与出生重的关系,改变某一性状,就会引起另一性状也发生变异但是断奶重并仅仅与出生重有关,还受遗传、饲养、管理、疾病等多方面因素的影响,因此,二者不是一一对应的函数关系。但是还存在着必然的联系。例如:奶的产奶量越高,乳脂率反而减少猪、鸡的生长速度越快,肉质和风味下降。母猪的体重越大,仔猪出生重越大
(2)非确定的关系,不是一一对应的函数关系,不能用公 式来表示。 如:仔猪断奶重与出生重的关系,改变某一性状,就 会引起另一性状也发生变异。 但是断奶重并仅仅与出生重有关,还受遗传、饲养、 管理、疾病等多方面因素的影响。 因此,二者不是一一对应的函数关系。但是还存在着 必然的联系。 例如:奶牛的产奶量越高,乳脂率反而减少。 猪、鸡的生长速度越快,肉质和风味下降。 母猪的体重越大,仔猪出生重越大

相关关系(relationship)统计学将这种非确定的关系称为统计相关关系生物的性状一般都属于这种关系(1)7相关关系(correlation)研究变量间关系的强弱程度,变量间的地位是平等的,无因果关系。(2)回归关系(regression)变量间的关系是因果关系,由某种变量的变化去估计或预测另一些变量的变化。一元相关、一元回归;多元相关、多元回归
相关关系(relationship): 统计学将这种非确定的关系称为统计相关关系, 生物的性状一般都属于这种关系。 (1)相关关系(correlation): 研究变量间关系的强弱程度,变量间的地位是平等的, 无因果关系。 (2)回归关系(regression): 变量间的关系是因果关系,由某种变量的变化去估计或 预测另一些变量的变化。 一元相关、一元回归;多元相关、多元回归

相关与回归的主要区别相关:定性分析“有或无”,非确定性的关系侧重二者之间的关系。x与y之间是平等的,回归:定量分析“y=a+bx”,在相关的基础上进行进一步的分析,自变量与依变量有从属之分
相关与回归的主要区别 相关:定性分析 “有或无”,非确定性的关系, x与y之间是平等的,侧重二者之间的关系。 回归:定量分析 “y=a+bx”,在相关的基础上 进行进一步的分析,自变量与依变量有 从属之分
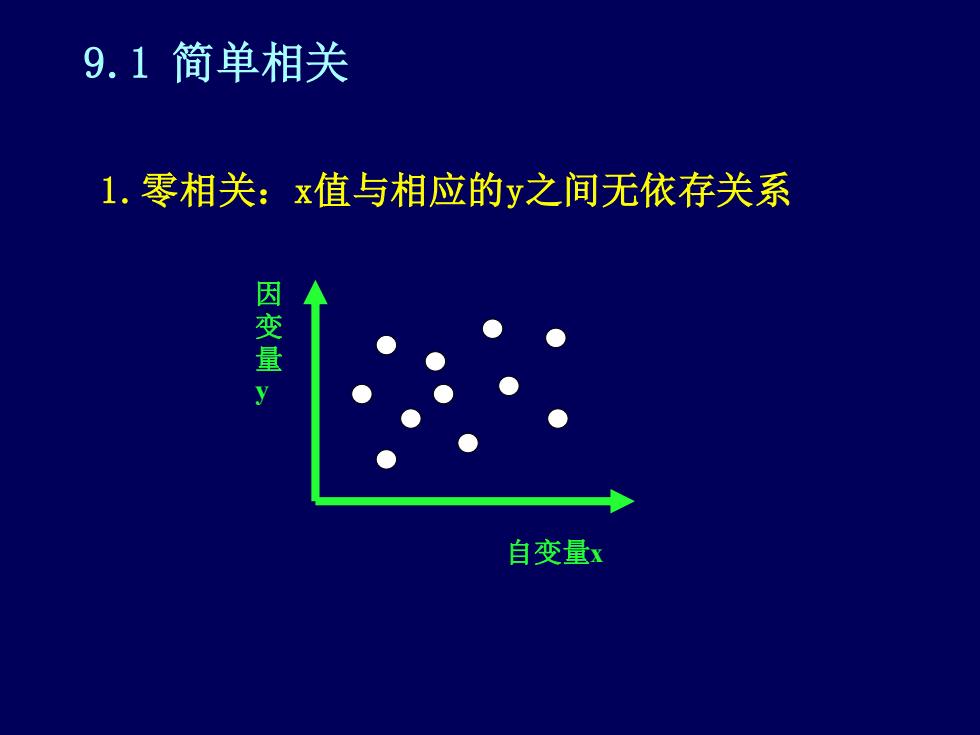
9.1 简单相关1.零相关:x值与相应的y之间无依存关系因变量自变量x
9.1 简单相关 1.零相关:x值与相应的y之间无依存关系 自变量x 因 变 量 y
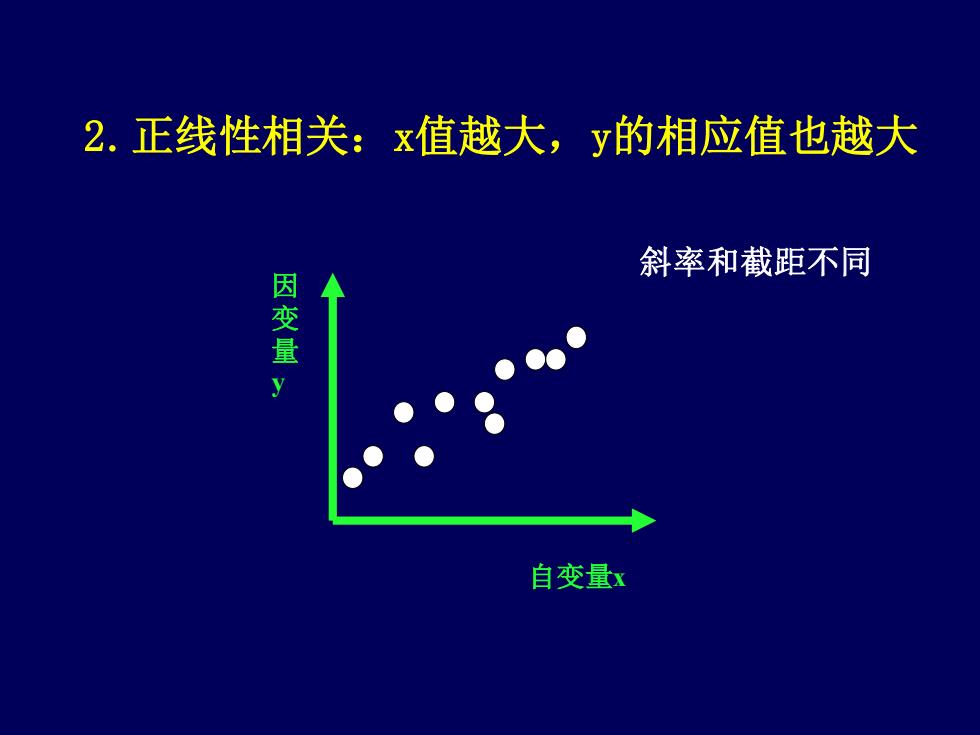
2.正线性相关:x值越大,y的相应值也越大斜率和截距不同因变量自变量x
自变量x 因 变 量 y 2.正线性相关:x值越大,y的相应值也越大 斜率和截距不同
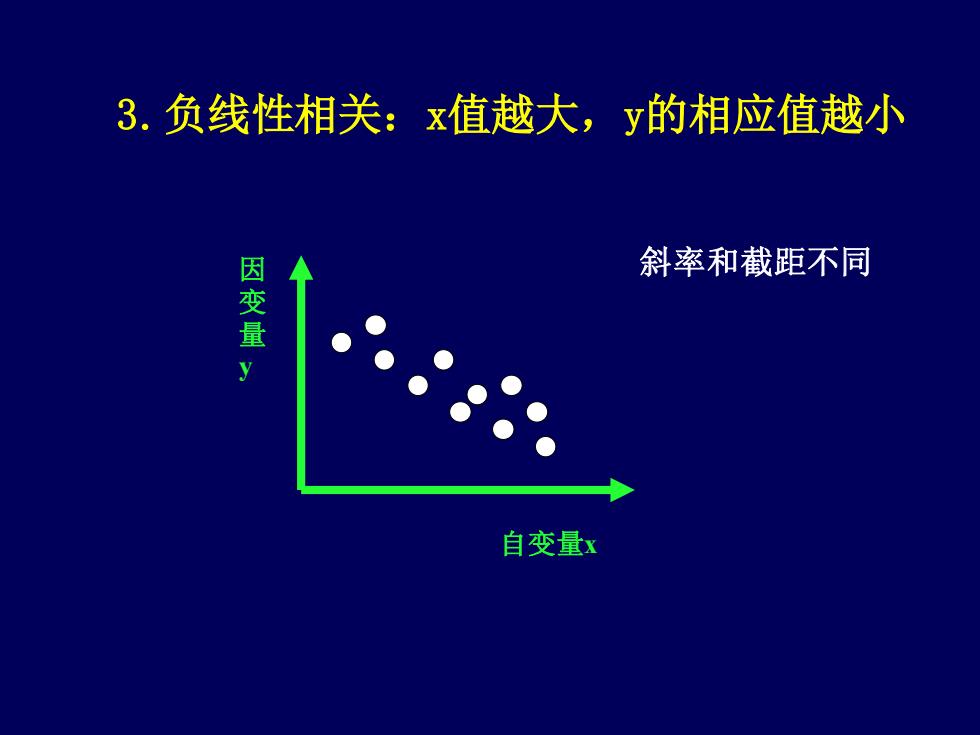
3.负线性相关:x值越大,y的相应值越小斜率和截距不同因变量自变量x
3.负线性相关:x值越大,y的相应值越小 自变量x 因 变 量 y 斜率和截距不同
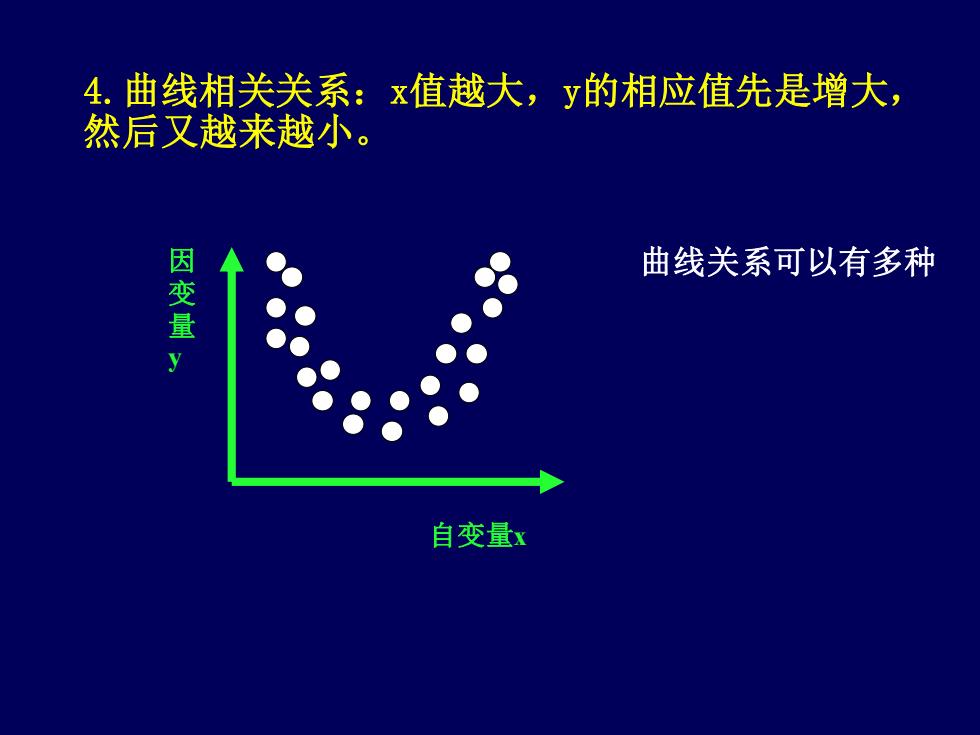
4.曲线相关关系:x值越大,y的相应值先是增大然后又越来越小。因变量曲线关系可以有多种自变量x
4.曲线相关关系:x值越大,y的相应值先是增大, 然后又越来越小。 自变量x 因 变 量 y 曲线关系可以有多种

9. 1. 1 7样本相关系数的定义相关系数的意义是一个常数。不仅能够代表两个变量之间的相关关系的性质,而且还能度量相关的紧密程度。用r表示
相关系数的意义 是一个常数。不仅能够代表两个变量之间 的相关关系的性质,而且还能度量相关的紧密 程度。 用 r 表示 9.1.1 样本相关系数的定义

1.离均差乘积和,简称乘积和。E(X -X)(Y-Y)SPxY=乘积和:正值,X与Y为正线性相关关系;负值,X与Y为负线性相关关系。绝对值越大,线性相关关系越强。所以,乘积和可以用来度量两个变量之间的线性相关关系。但是与样本含量有关。为了消除样本含量的影响,可以除以自由度
SP = (X − X)(Y −Y) XY 1. 离均差乘积和,简称乘积和。 乘积和: 正值,X与Y为正线性相关关系;负值,X与Y为负线性 相关关系。 绝对值越大,线性相关关系越强。 所以,乘积和可以用来度量两个变量之间的线性相关关 系。但是与样本含量有关。 为了消除样本含量的影响,可以除以自由度