第三章 烯烃和二烯烃
第三章 烯烃和二烯烃

第一节 烯烃 第二节 二烯烃
第一节 烯烃 第二节 二烯烃

第一节 烯烃 一 、烯烃的通式和异构现象 (一) 烯烃的通式 分子中只含有一个碳碳双(或三)键的链烃叫做 单烯(或炔)烃。单烯烃比相应烷烃少两个氢原子, 通式为CnH2n
第一节 烯烃 一 、烯烃的通式和异构现象 (一) 烯烃的通式 分子中只含有一个碳碳双(或三)键的链烃叫做 单烯(或炔)烃。单烯烃比相应烷烃少两个氢原子, 通式为CnH2n

烯烃由于碳架不同和双键在碳架上的 位置不同而有各种构造异构体。 如丁烯的三个同分异构体为: (二) 烯烃的异构现象 ① ② ③ CH2 CHCH2CH3 CH2 C CH3 CH3 CH3CH CHCH3 其中 ①或③和②互为碳链异构体. ①和③互为位置异构体
烯烃由于碳架不同和双键在碳架上的 位置不同而有各种构造异构体。 如丁烯的三个同分异构体为: (二) 烯烃的异构现象 ① ② ③ CH2 CHCH2CH3 CH2 C CH3 CH3 CH3CH CHCH3 其中 ①或③和②互为碳链异构体. ①和③互为位置异构体
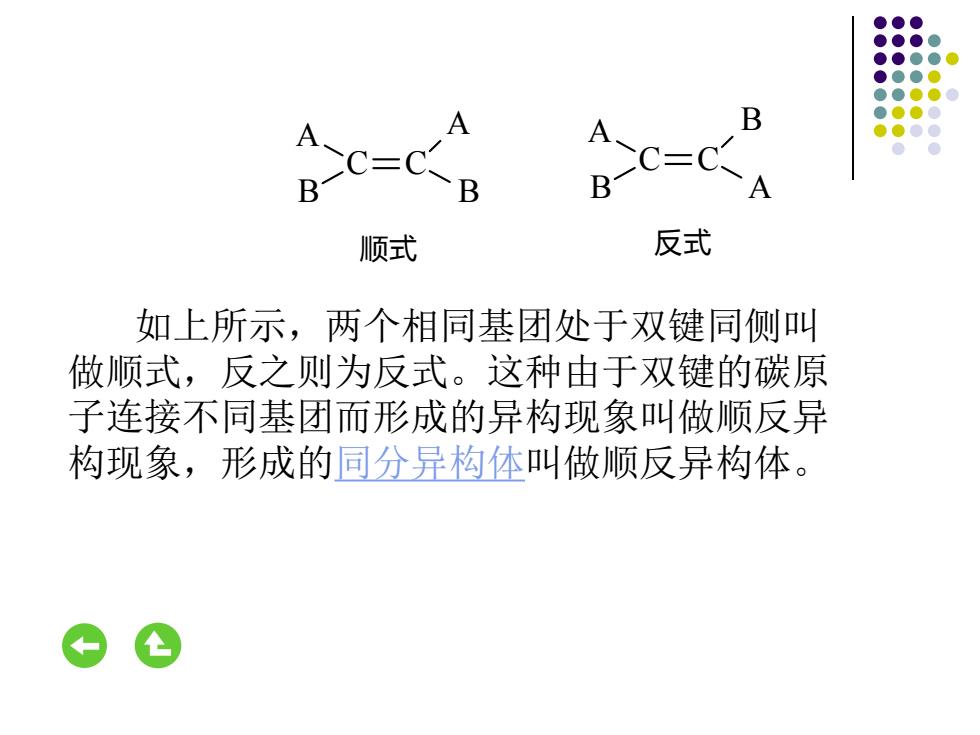
如上所示,两个相同基团处于双键同侧叫 做顺式,反之则为反式。这种由于双键的碳原 子连接不同基团而形成的异构现象叫做顺反异 构现象,形成的同分异构体叫做顺反异构体。 C C A B A B C C B A A B 顺式 反式
如上所示,两个相同基团处于双键同侧叫 做顺式,反之则为反式。这种由于双键的碳原 子连接不同基团而形成的异构现象叫做顺反异 构现象,形成的同分异构体叫做顺反异构体。 C C A B A B C C B A A B 顺式 反式

孤立二烯烃 CH2 CH CH2 CH CH2 共轭二烯烃 CH2 CH CH CH2 (2) 二烯烃的通式和分类 分子中含有两个碳碳双键的链烃叫做二烯烃。 通式为CnH2n-2。根据二烯烃分子中两个碳碳双 键的相对位置不同分类: C H 2 C C H 2 二烯烃 累积二烯烃 (丙二烯) (1,3-丁二烯) (1,4-戊二烯)
孤立二烯烃 CH2 CH CH2 CH CH2 共轭二烯烃 CH2 CH CH CH2 (2) 二烯烃的通式和分类 分子中含有两个碳碳双键的链烃叫做二烯烃。 通式为CnH2n-2。根据二烯烃分子中两个碳碳双 键的相对位置不同分类: C H 2 C C H 2 二烯烃 累积二烯烃 (丙二烯) (1,3-丁二烯) (1,4-戊二烯)
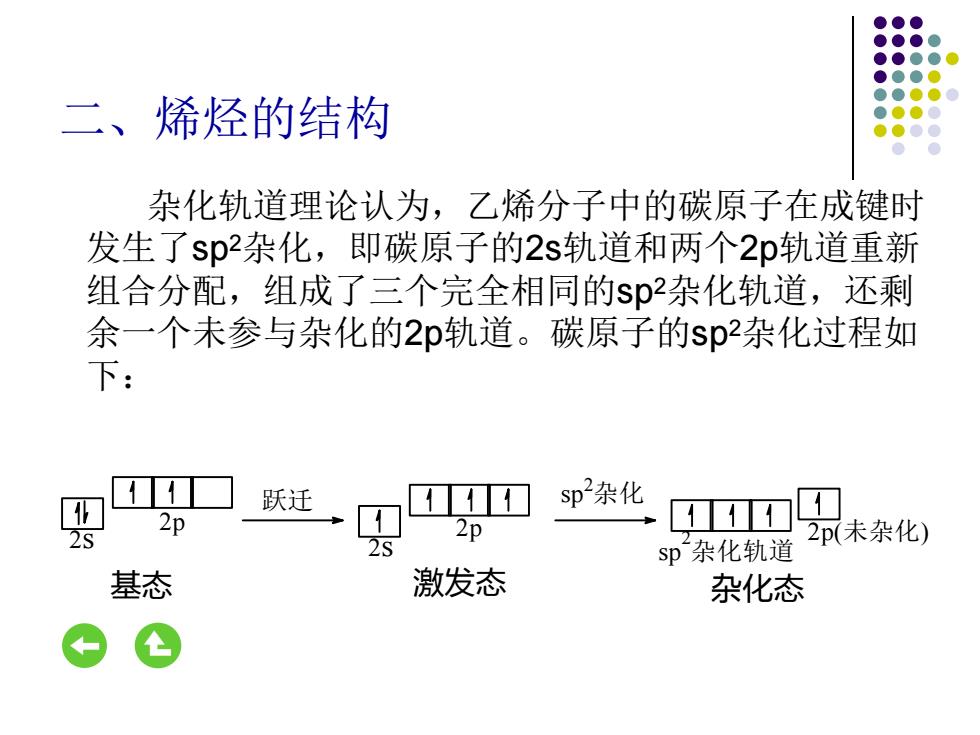
二、烯烃的结构 杂化轨道理论认为,乙烯分子中的碳原子在成键时 发生了sp2杂化,即碳原子的2s轨道和两个2p轨道重新 组合分配,组成了三个完全相同的sp2杂化轨道,还剩 余一个未参与杂化的2p轨道。碳原子的sp2杂化过程如 下: 2p(未杂化) 基态 激发态 杂化态 sp 2杂化 sp 2杂化轨道 跃迁 2p 2p 2s 2s
二、烯烃的结构 杂化轨道理论认为,乙烯分子中的碳原子在成键时 发生了sp2杂化,即碳原子的2s轨道和两个2p轨道重新 组合分配,组成了三个完全相同的sp2杂化轨道,还剩 余一个未参与杂化的2p轨道。碳原子的sp2杂化过程如 下: 2p(未杂化) 基态 激发态 杂化态 sp 2杂化 sp 2杂化轨道 跃迁 2p 2p 2s 2s

sp2轨道模型
sp2轨道模型

三、烯烃的命名 (一)烯基的命名 烯烃去掉一个H后的一价基团. 烯基在命 名时, 其编号应从游离价所在的C开始。 CH2=CH- 乙烯基 -CH2CH=CH2 烯丙基 (或 2–丙烯基) CH3CH=CH- 丙烯基 (或 1–丙烯基) CH3C=CH2 异丙烯基
三、烯烃的命名 (一)烯基的命名 烯烃去掉一个H后的一价基团. 烯基在命 名时, 其编号应从游离价所在的C开始。 CH2=CH- 乙烯基 -CH2CH=CH2 烯丙基 (或 2–丙烯基) CH3CH=CH- 丙烯基 (或 1–丙烯基) CH3C=CH2 异丙烯基

2. 乙烯的结构和π键 乙烯分子形成时,两个碳原子各以一个sp2杂化 轨道沿键轴方向重叠形成一个C—Cσ键,并以剩余 的两个sp2杂化轨道分别与两个氢原子的1s轨道沿键 轴方向重叠形成4个等同的C—Hσ键,5个σ键都在 同一平面内,因此乙烯为平面构型。此外,每个碳 原子上还有一个未参与杂化的p轨道,两个碳原子的 p轨道相互平行,于是侧面重叠(也称为“肩并肩” 重叠)成键。这种成键原子的p轨道平行侧面重叠形 成的共价键叫做π键
2. 乙烯的结构和π键 乙烯分子形成时,两个碳原子各以一个sp2杂化 轨道沿键轴方向重叠形成一个C—Cσ键,并以剩余 的两个sp2杂化轨道分别与两个氢原子的1s轨道沿键 轴方向重叠形成4个等同的C—Hσ键,5个σ键都在 同一平面内,因此乙烯为平面构型。此外,每个碳 原子上还有一个未参与杂化的p轨道,两个碳原子的 p轨道相互平行,于是侧面重叠(也称为“肩并肩” 重叠)成键。这种成键原子的p轨道平行侧面重叠形 成的共价键叫做π键