银川能源学院（银川大学）：《大学物理》课程教学资源（PPT课件讲稿）第一篇 力学基础 第3章 刚体力学基础

第3章刚体力学基出 ，§3.1刚体刚体定轴转动的描述 )§3.2刚体定轴转动的转动定律 )§3.3刚体定轴转动的动能定理 >§3.4刚体定轴转动的角动量定理和角动量 守恒定律 A下A

------------------------------------------------------------------------------- 第3章 刚体力学基础 §3.1 刚体 刚体定轴转动的描述 §3.2 刚体定轴转动的转动定律 §3.3 刚体定轴转动的动能定理 §3.4 刚体定轴转动的角动量定理和角动量 守恒定律

刚体力学的基础知识包括刚体绕定轴转 动的动力学方程和动能定理，刚体绕定轴 转动的角动量定理及角动量守恒定律

------------------------------------------------------------------------------- 刚体力学的基础知识包括刚体绕定轴转 动的动力学方程和动能定理，刚体绕定轴 转动的角动量定理及角动量守恒定律

§3-1刚体刚体定轴转动的描述 刚体，指在任何情况下都没有形变的物体 一、刚体定轴转动的描述 1.平动和转动 刚体在运动中，其上任意两点的连线始终保持平行 如果物体上的所有质元都绕某同一直线作圆周运 动，这种运动就称之为转动，这条直线称为转轴

------------------------------------------------------------------------------- §3-1 刚体 刚体定轴转动的描述 刚体，指在任何情况下都没有形变的物体 一、刚体定轴转动的描述 1.平动和转动 刚体在运动中，其上任意两点的连线始终保持平行 如果物体上的所有质元都绕某同一直线作圆周运 动，这种运动就称之为转动，这条直线称为转轴

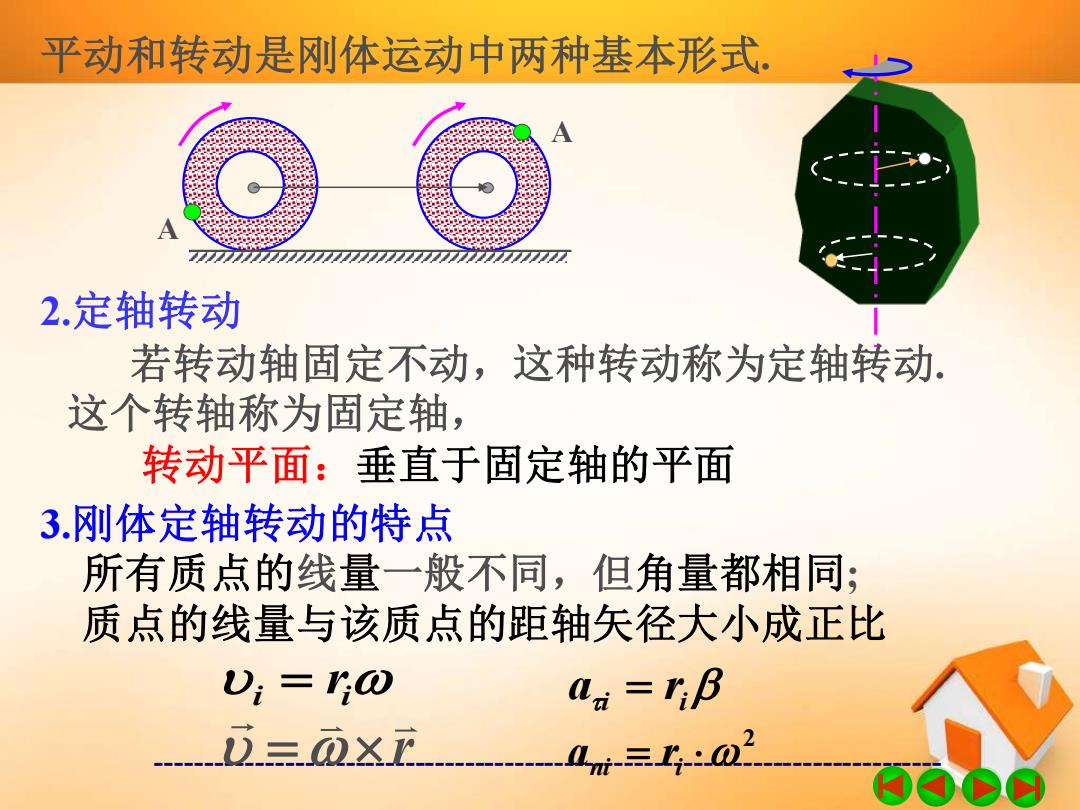
平动和转动是刚体运动中两种基本形式： 2.定轴转动 若转动轴固定不动，这种转动称为定轴转动， 这个转轴称为固定轴， 转动平面：垂直于固定轴的平面 3.刚体定轴转动的特点 所有质点的线量一般不同，但角量都相同； 质点的线量与该质点的距轴矢径大小成正比 D:=0 aa=rB 2.=瓦X正 0-=1-:03

------------------------------------------------------------------------------- 平动和转动是刚体运动中两种基本形式. A A 若转动轴固定不动，这种转动称为定轴转动. 这个转轴称为固定轴， 2.定轴转动 转动平面：垂直于固定轴的平面 3.刚体定轴转动的特点 所有质点的线量一般不同，但角量都相同; 质点的线量与该质点的距轴矢径大小成正比 i = ri  ai = ri  2 r ani = ri      =

>刚体的一般运动 质心的平动十 绕质心的转动 播放 暂停 返回 QODA

------------------------------------------------------------------------------- ➢ 刚体的一般运动 质心的平动 + 绕质心的转动

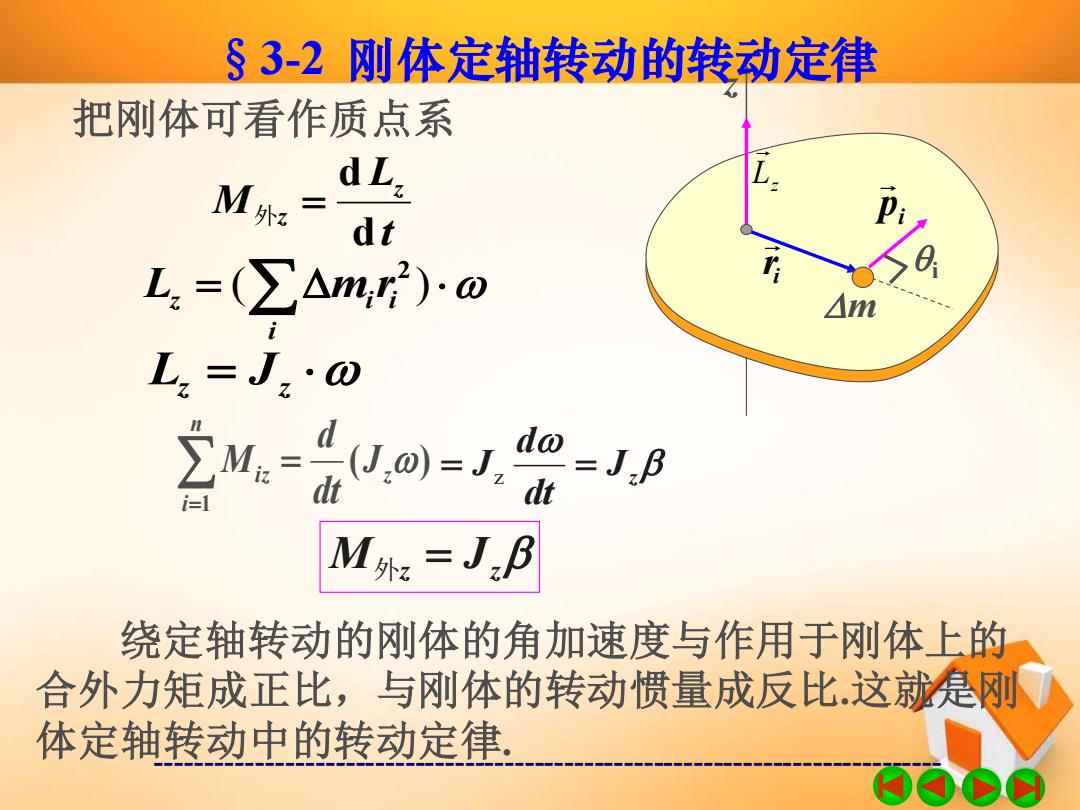
§3-2刚体定轴转动的转动定律 把刚体可看作质点系 M外z= dL: dt L,=(∑△m,)o △m L2=J2·0 M外：=JB 绕定轴转动的刚体的角加速度与作用于刚体上的 合外力矩成正比，与刚体的转动惯量成反比.这就是刚 体定轴转动中的转动定律

------------------------------------------------------------------------------- 把刚体可看作质点系 Lz  z i r  m i i p  t L M z z d d 外 = = ( ) i z i i L m r 2 Lz = Jz  ( ) 1 z  n i iz J dt d  M = =   Jz dt d = Jz = M外z = Jz  绕定轴转动的刚体的角加速度与作用于刚体上的 合外力矩成正比，与刚体的转动惯量成反比.这就是刚 体定轴转动中的转动定律. §3-2 刚体定轴转动的转动定律

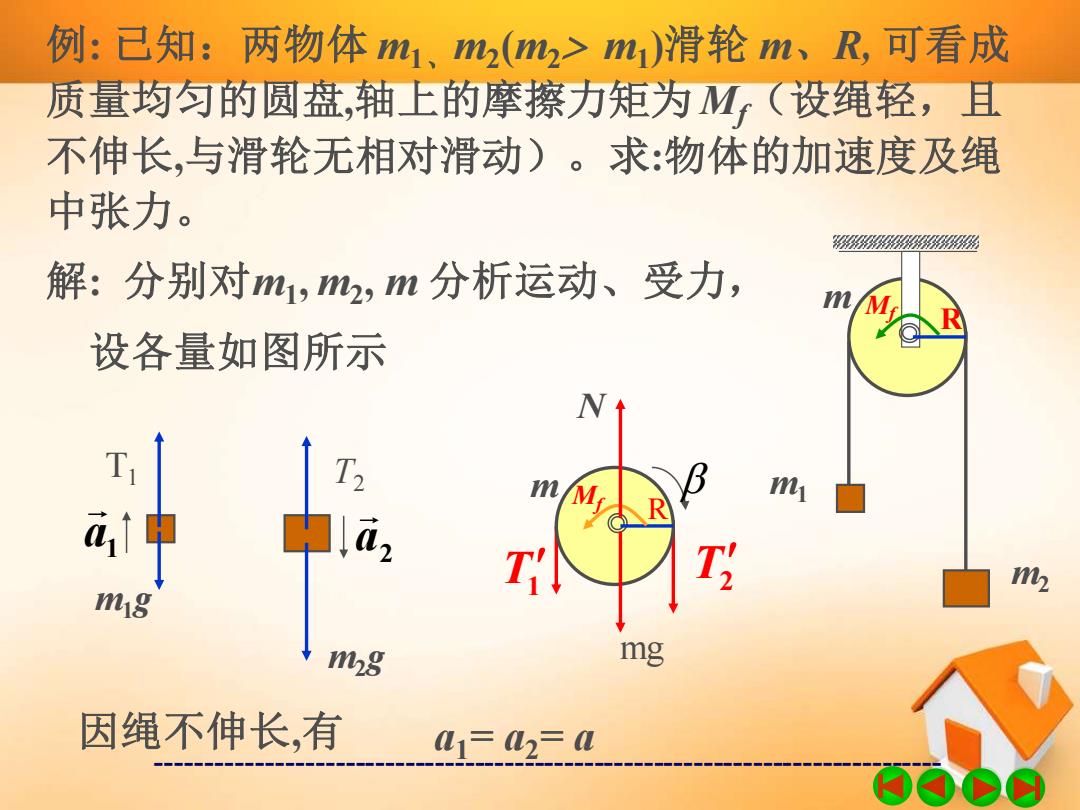
例：已知：两物体m1、m2(m2>m1)滑轮m、R,可看成 质量均匀的圆盘，轴上的摩擦力矩为M(设绳轻，且 不伸长，与滑轮无相对滑动)。求：物体的加速度及绳 中张力。 解：分别对m1,m2,m分析运动、受力， 设各量如图所示 R 白 T T 2 m18 mg mg 因绳不伸长，有 L1=2=M

------------------------------------------------------------------------------- 例: 已知：两物体 m1、 m2 (m2 m1 )滑轮 m、R, 可看成 质量均匀的圆盘,轴上的摩擦力矩为 Mf（设绳轻，且 不伸长,与滑轮无相对滑动）。求:物体的加速度及绳 中张力。 m1 m2 m R Mf 解: 分别对m1 , m2 , m 分析运动、受力， 设各量如图所示 1 a  m1g T1 a2  m2g T2  T2  T1  m R Mf mg N 因绳不伸长,有 a1= a2= a

因绳轻，有T=T,T2=T 以加速度方向为正，可列出 对m1有：T1-m1g=m10 (1) 对m2有：m2g-T2=m2a (2) 对滑轮m由转动方程 R-TR-Mr=JB=2欧 (3) 再从运动学关系上有 a=a=RB (4) (以“B方向”为正) D同

------------------------------------------------------------------------------- 因绳轻,有 T1 T1 T2 T2 =  , =  以加速度方向为正，可列出 对m1有: T1 - m1g = m1a (1) 对 m2有： m2g - T2= m2 a (2) 对滑轮 m 由转动方程   2 2 1 2 1 T R −T R − M f = J = mR (3) 再从运动学关系上有 a = a = R (4) (以“方向”为正)

联立四式解得： a= m,m-是 mmm mM, R m +2 m1+m2 mM R m1+m,+2 当不计滑轮质量和摩擦力矩时： m=0,Mr=0 m-mg T=T= 22g m2+m1 m1+m2 冈

------------------------------------------------------------------------------- 联立四式解得： ( ) m m m R M m m g a f 2 1 1 2 2 1 + + − − = ( ) 2 2 2 1 2 1 2 1 1 1 m m m R m M m g m m T m g a f + +  −      + = + = ( ) 2 2 2 1 2 2 1 2 2 2 m m m R m M m g m m T m g a f + +  +      + = − = 当不计滑轮质量和摩擦力矩时: m = 0, Mf = 0 g m m m m a 2 1 2 1 + − = g m m m m T T 1 2 1 2 1 2 2 + = =

§3-31 刚体定轴转动的动能定理 1.转动动能 E,=∑Am,ia2-2∑amia2 刚体绕定轴转动时的转动动能等于刚体的转动 惯量与角速度平方乘积的一半 比较： Ek= Jo' 2 2J E 2 2m

------------------------------------------------------------------------------- 1.转动动能 2 2 2 2 ( ) 2 1 2 1 Ek =  mi ri  = mi ri  2 2 1 Ek = J 刚体绕定轴转动时的转动动能等于刚体的转动 惯量与角速度平方乘积的一半 比较： J L Ek 2 2 = m p Ek 2 2 = 2 2 1 Ek = m 2 2 1 Ek = J §3-3 刚体定轴转动的动能定理