
第2章质点动力学 §2.1 牛顿运动定律 §2.2 动量动量守恒定律 )§2.3功动能势能机械能守恒定律 人§2.4角动量角动量守恒定律 QODA
------------------------------------------------------------------------------- 第2章 质点动力学 §2.1 牛顿运动定律 §2.2 动量 动量守恒定律 §2.3 功 动能 势能 机械能守恒定律 §2.4 角动量 角动量守恒定律

物体间的相互作用称为力,研究 物体在力的作用下运动的规律称为 动力学
------------------------------------------------------------------------------- 物体间的相互作用称为力,研究 物体在力的作用下运动的规律称为 动力学

§2-1牛顿运动定律 一、惯性定律 惯性参考系 1.牛顿第一定律 一孤立质点将永远保持其原来静止或匀速直线运 动状态. 牛顿第一定律又称为惯性定律。 意义: ()定性给出了两个重要概念,力与惯性 力是物体与物体间的相互作用. 惯性是物体的固有属性. (2)定义了惯性参考系 惯性定律成立的参照系为惯性系
------------------------------------------------------------------------------- 一、惯性定律 惯性参考系 1.牛顿第一定律 一孤立质点将永远保持其原来静止或匀速直线运 动状态. 牛顿第一定律又称为惯性定律. 意义: (1) 定性给出了两个重要概念,力与惯性 力是物体与物体间的相互作用. 惯性是物体的固有属性. (2) 定义了惯性参考系 惯性定律成立的参照系为惯性系。 §2-1 牛顿运动定律
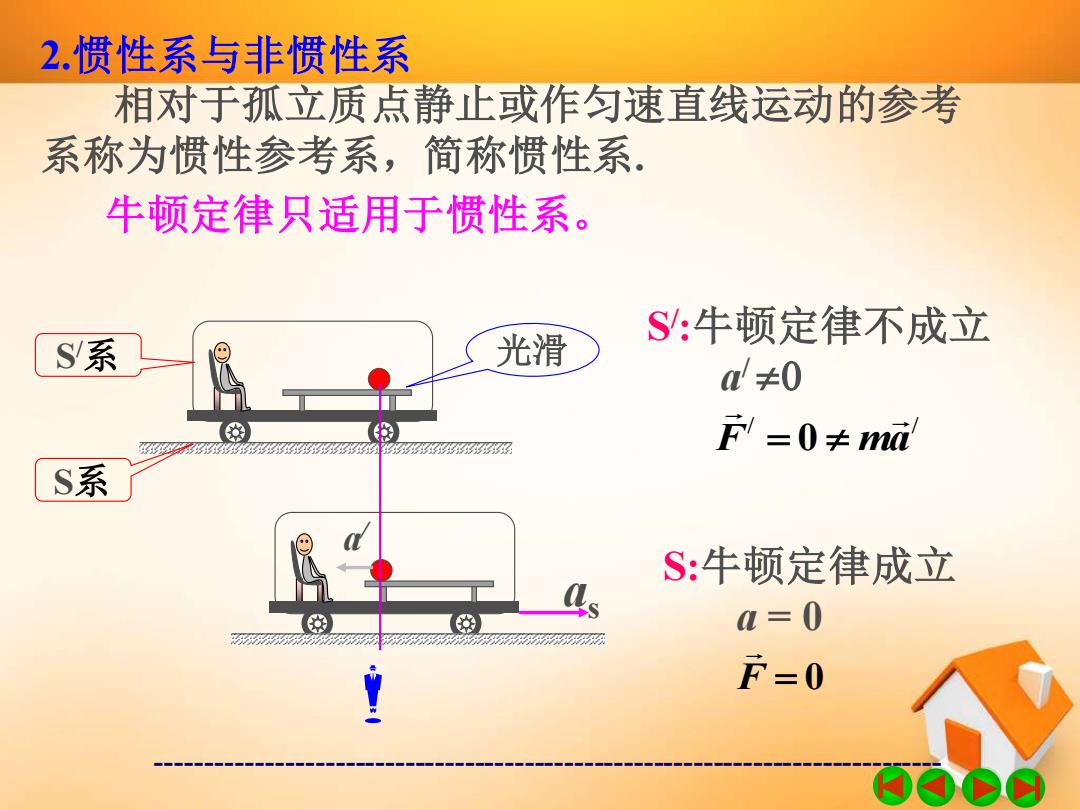
2.惯性系与非惯性系 相对于孤立质点静止或作匀速直线运动的参考 系称为惯性参考系,简称惯性系 牛顿定律只适用于惯性系。 S:牛顿定律不成立 S系 光滑 ≠0 g钢 F=0≠md S系 S:牛顿定律成立 a=0 F=0
------------------------------------------------------------------------------- 2.惯性系与非惯性系 相对于孤立质点静止或作匀速直线运动的参考 系称为惯性参考系,简称惯性系. 牛顿定律只适用于惯性系。 as a / S /系 S系 光滑 S / :牛顿定律不成立 a / 0 / / F ma = 0 S:牛顿定律成立 a = 0 F = 0

①确定惯性系一只有通过力学实验 根据天文观察,以太阳系作为参照系研究行星 运动时发现行星运动遵守牛顿定律,所以太阳系是 一个惯性系。 ②相对于已知惯性系作匀速直线运动的参照系也 是惯性系 非惯性系:相对于已知惯性系作加速运动的参照系
------------------------------------------------------------------------------- ① 确定惯性系──只有通过力学实验 根据天文观察,以太阳系作为参照系研究行星 运动时发现行星运动遵守牛顿定律,所以太阳系是 一个惯性系。 ② 相对于已知惯性系作匀速直线运动的参照系也 是惯性系 非惯性系:相对于已知惯性系作加速运动的参照系

二、牛顿第二定律 物体受到外力作用时,它所获得的加速度的 大小与合外力的大小成正比,与物体的质量成反 比;加速度的方向与合外力F的方向相同 F=ma 瞬时性:第二定律是力的瞬时作用规律 下、之间一一对应 矢量性:有大小和方向,可合成与分解 力的叠加原理 F=F+月+…+F=∑F
------------------------------------------------------------------------------- 二、牛顿第二定律 物体受到外力作用时,它所获得的加速度的 大小与合外力的大小成正比,与物体的质量成反 比;加速度的方向与合外力F的方向相同 F ma = 瞬时性:第二定律是力的瞬时作用规律 F a 、 之间一一对应 矢量性:有大小和方向,可合成与分解 力的叠加原理 = = + + + = i N F F F FN Fi 1 1 2

分解: ∑F=m=m vx d 直角坐标系中: 了∑F,=ma,=m ∑F=ma= dv dt 自然坐标系中: ∑F,=m 2∑E=m p 定量的量度了惯性: m4=号 p ms A ①质量是物体惯性大小的量度; ② 引力质量:F-G元 QODA
------------------------------------------------------------------------------- 分解: dt d F ma m y y y = = dt d F ma m x x x = = dt d F ma m z z z = = 直角坐标系中: dt d F m = 2 自然坐标系中: Fn = m 定量的量度了惯性: A B B A a a m m = ① 质量是物体惯性大小的量度; ② 引力质量: 2 0 r r GMm F =

三、牛顿第三定律 当物体A以力F作用在物体B上时,物体B也必定 同时以力F,作用在物体A上.F和F,大小相等,方向 相反,且力的作用线在同一直线上 F=-F 作用力与反作用力 ①总是成对出现,一一对应的. ②不是一对平衡力. ③是属于同一性质的力 说明: 若相对论效应不能忽略时,牛顿第三定律的这种 表达就失效了,这时取而代之的是动量守恒定律
------------------------------------------------------------------------------- 三、牛顿第三定律 当物体A以力F1作用在物体B上时,物体B也必定 同时以力F2作用在物体A上.F1和F2大小相等,方向 相反,且力的作用线在同一直线上. 作用力与反作用力: ①总是成对出现,一一对应的. ②不是一对平衡力. ③是属于同一性质的力. 说明: 若相对论效应不能忽略时,牛顿第三定律的这种 表达就失效了,这时取而代之的是动量守恒定律. F1 F2 = −

四、牛顿定律的应用 解题思路: (1)选取对象 (2)分析运动 (轨迹、速度、加速度) (3)分析受力(隔离物体、画受力图) (4)列出方程(标明坐标的正方向; 从运动关系上补方程) (5)讨论结果(量纲?特例?等) QOOA
------------------------------------------------------------------------------- 四、牛顿定律的应用 解题思路: (1)选取对象 (2)分析运动(轨迹、速度、加速度) (3)分析受力(隔离物体、画受力图) (4)列出方程(标明坐标的正方向; 从运动关系上补方程) (5)讨论结果(量纲?特例?等)
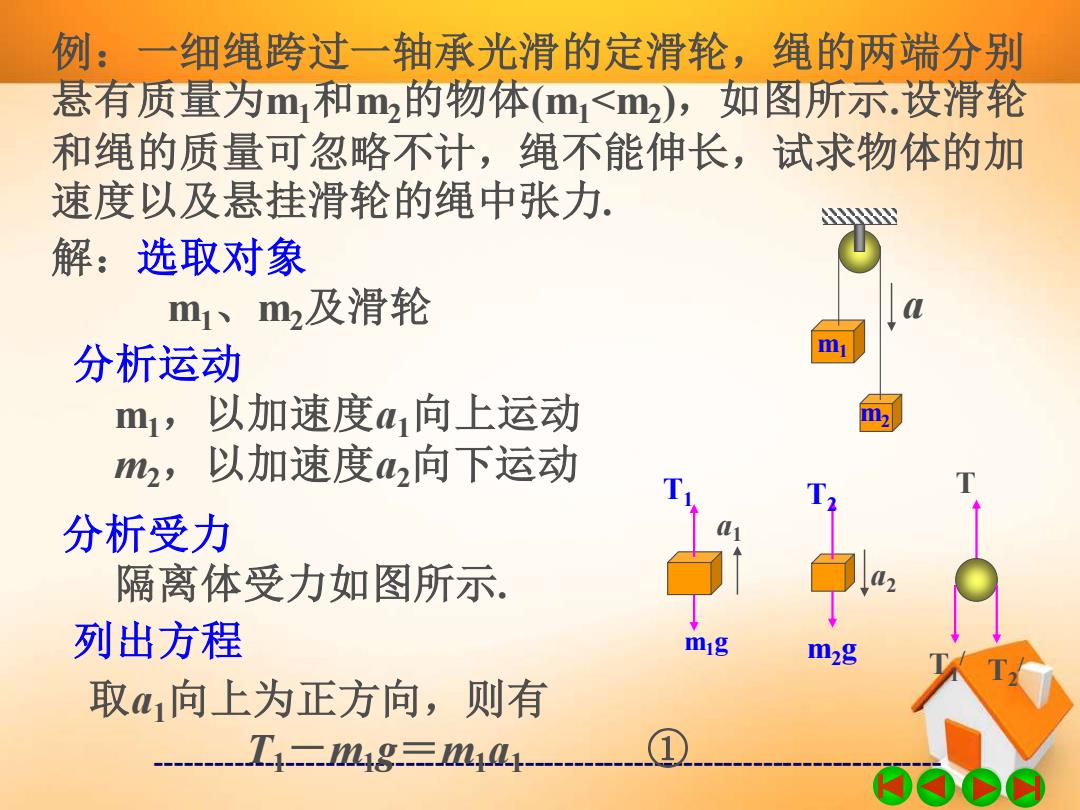
例:一细绳跨过一轴承光滑的定滑轮,绳的两端分别 悬有质量为m1和m2的物体(m<m2),如图所示.设滑轮 和绳的质量可忽略不计,绳不能伸长,试求物体的加 速度以及悬挂滑轮的绳中张力. 解:选取对象 m1、m2及滑轮 分析运动 m1,以加速度a1向上运动 m2,以加速度2向下运动 分析受力 隔离体受力如图所示。 列出方程 mig m2g 取1向上为正方向,则有 工-48三44
------------------------------------------------------------------------------- 例:一细绳跨过一轴承光滑的定滑轮,绳的两端分别 悬有质量为m1和m2的物体(m1<m2 ),如图所示.设滑轮 和绳的质量可忽略不计,绳不能伸长,试求物体的加 速度以及悬挂滑轮的绳中张力. 解:选取对象 m1、m2及滑轮 分析运动 m1,以加速度a1向上运动 m2,以加速度a2向下运动 分析受力 隔离体受力如图所示. 列出方程 取a1向上为正方向,则有 T1-m1g=m1a1 ① a m1 m2 m1g a1 T1 m2g T2 a2 T1 / T2 / T