
第1章, 质点运动学 §1.1 参考系坐标系物理模型 §1.2 位矢、位移、速度及加速度 §1.3 0 曲线运动的描述 b§1.4 运动学中的两类问题 )§1.5相对运动* IA①A
------------------------------------------------------------------------------- 第1章 质点运动学 §1.1 参考系 坐标系 物理模型 §1.2 位矢、位移、速度及加速度 §1.3 曲线运动的描述 §1.4 运动学中的两类问题 §1.5 相对运动*

运动学是从几何的观点来描述物体的 运动,即研究物体的空间位置随时间的变 化关系,不涉及引发物体运动和改变运动 状态的原因
------------------------------------------------------------------------------- 运动学是从几何的观点来描述物体的 运动,即研究物体的空间位置随时间的变 化关系,不涉及引发物体运动和改变运动 状态的原因

§1-1参考系坐标系物理模型 一、运动的绝对性和相对性 运动是绝对的: 任何物体任何时刻都在不停地运动着 运动又是相对的: 运动的描述是相对其他物体而言的
------------------------------------------------------------------------------- 一、运动的绝对性和相对性 运动是绝对的: 任何物体任何时刻都在不停地运动着 运动又是相对的: 运动的描述是相对其他物体而言的。 §1-1 参考系 坐标系物理模型

二、参考系 为描述物体的运动,被选作基准的物体或物体系 称为参考系。 运动学中参考系可任选 常用的参考系: ▲太阳参考系(太阳一恒星参考系)
------------------------------------------------------------------------------- 二、参考系 为描述物体的运动,被选作基准的物体或物体系 称为参考系 。 运动学中参考系可任选 ▲ 太阳参考系(太阳 ─ 恒星参考系) 常用的参考系:
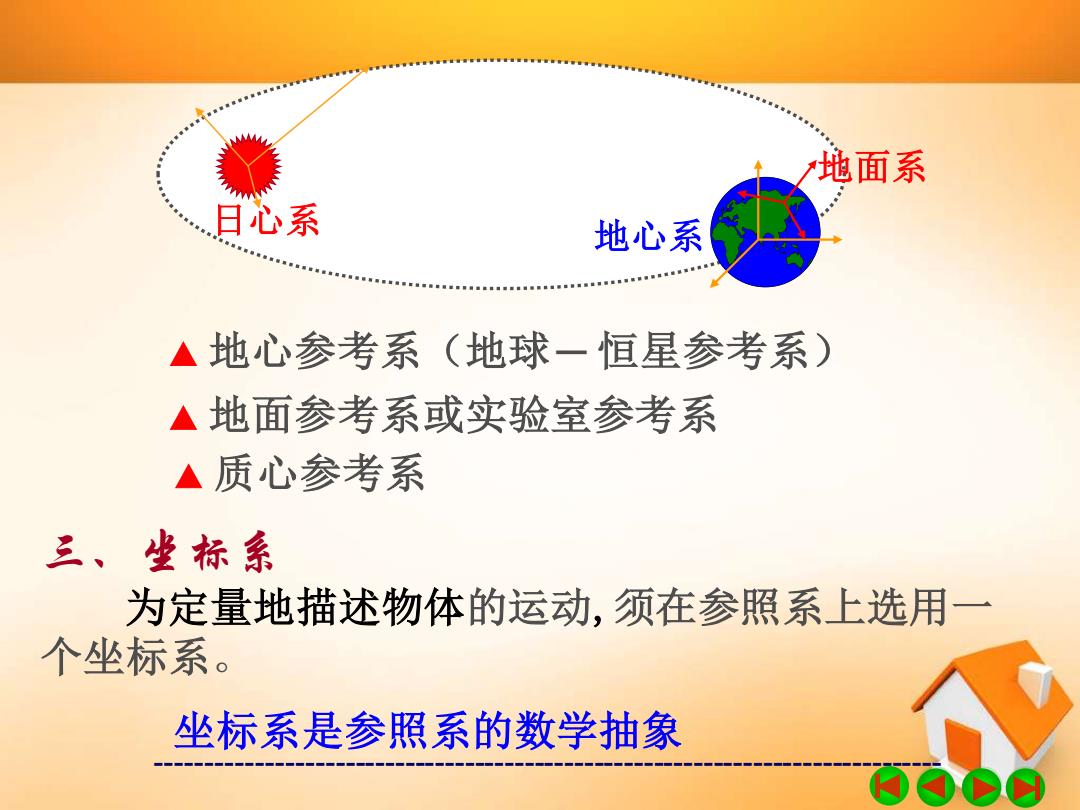
地面系 日心系 地心系 ■ ▲地心参考系(地球一恒星参考系) ▲地面参考系或实验室参考系 ▲质心参考系 三、坐标系 为定量地描述物体的运动,须在参照系上选用一 个坐标系。 坐标系是参照系的数学抽象
------------------------------------------------------------------------------- 日心系 ▲ 地心参考系(地球─ 恒星参考系) 地心系 ▲ 地面参考系或实验室参考系 地面系 ▲ 质心参考系 三、坐标系 为定量地描述物体的运动,须在参照系上选用一 个坐标系。 坐标系是参照系的数学抽象

代21 e 0 X Z B 、S>0 B A <0 QODO
------------------------------------------------------------------------------- x y z 0 (x,y,z) i j k r 0 x r P r e e r x y z P A nA B nB 0 s 0 B

四、物理模型 对真实的物理过程和对象,根据所讨论的问题的 基本要求对其进行理想化的简化,抽象为可以用数学 方法描述的理想模型。 质点模型:物体自身线度与所研究的物体运动的空 间范围比可以忽略;或者物体作平动。 真实的物体不满足上述条件则可将其视为质点系。 综上所述: 选择合适的参考系 以方便确定物体的运动性质; •建立恰当的坐标系. 以定量地描述物体的运动; 提出较准确的物理模型. 以确定所提问题最基本运动律
------------------------------------------------------------------------------- 四、物理模型 对真实的物理过程和对象,根据所讨论的问题的 基本要求对其进行理想化的简化,抽象为可以用数学 方法描述的理想模型。 质点模型: 物体自身线度与所研究的物体运动的空 间范围r比可以忽略;或者物体作平动。 真实的物体不满足上述条件则可将其视为质点系。 综上所述: •选择合适的参考系. 以方便确定物体的运动性质; •建立恰当的坐标系. 以定量地描述物体的运动; •提出较准确的物理模型. 以确定所提问题最基本运动律

§1-2位矢、位移、速度及加速度 一位置头量 由原点引向考察点的矢量。 表示为 直角坐标系中 r=xi+yj+ak F=vx2+y2+z2 cosa=于cosf=eos7=子 cos2 a+cos2 B+cos2y =1
------------------------------------------------------------------------------- 一.位置矢量 由原点引向考察点的矢量。 0 r r 表示为 §1-2 位矢、位移、速度及加速度 直角坐标系中 r xi yj zk = + + x y z 0 (x,y,z) i j k r 2 2 2 r = x + y + z r z γ r y β r x cosα = ,cos = ,cos = 1 2 2 2 cos α + cos β + cos γ =

运动方程和轨迹方程 质点在运动过程中,空间位置随时间变化的函数 式称为运动方程。 表示为: 下=F(t) 直角坐标系中 (t)=x(t)i+y(t)j+z(t)k x=x(t) 或 y=y(t) =(t) 运动方程是时间t的显函数。 质点在空间所经过的路径称为轨道(轨迹) 从运动方程中消去,即可得到轨道方程 轨道方程不是时间t显函数
------------------------------------------------------------------------------- 运动方程和轨迹方程 质点在运动过程中,空间位置随时间变化的函数 式称为运动方程。 表示为: r r(t) = 直角坐标系中 r t x t i y t j z t k ( ) = ( ) + ( ) + ( ) ( ) ( ) ( ) z z t y y t x x t = = = 或 运动方程是时间t的显函数。 质点在空间所经过的路径称为轨道(轨迹) 从运动方程中消去t,即可得到轨道方程 轨道方程不是时间t显函数
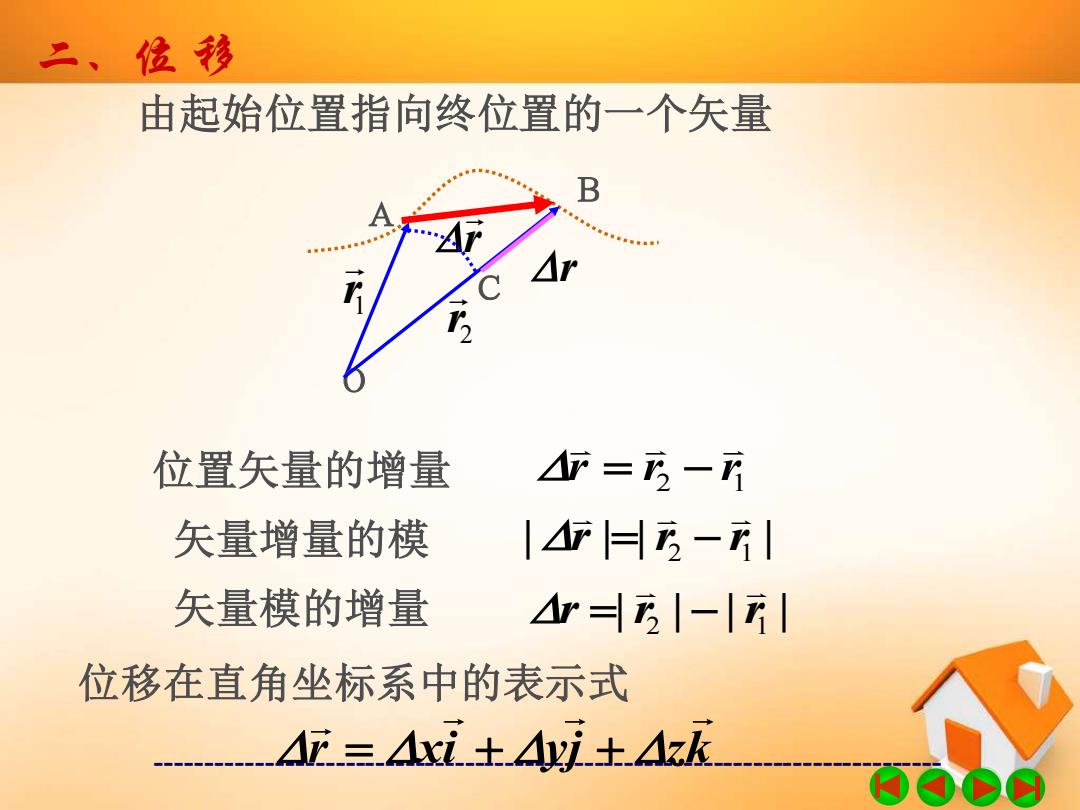
二、位移 由起始位置指向终位置的一个矢量 位置矢量的增量 你=店一 矢量增量的模 |4F曰2-所 矢量模的增量 -| 位移在直角坐标系中的表示式 4匠=.xi.土.±.人k
------------------------------------------------------------------------------- 二、位 移 由起始位置指向终位置的一个矢量 1 r O A 2 r B r 2 1 r r r 位置矢量的增量 = − | | | | 2 1 r r r 矢量增量的模 = − | | | | 2 1 r r r 矢量模的增量 = − C r 位移在直角坐标系中的表示式 r xi yj zk = + +