
银川川大学栽学镖件 物理学电子教案 静电场的环路定理、电势及其计算 1、静电场的环路定理 2、电势,电势能 3、电势的计算
物理学电子教案 银川大学教学课件 静电场的环路定理、电势及其计算 1、静电场的环路定理 2、电势,电势能 3、电势的计算

复习 ·电荷的量子化 电荷守恒定律 库仑定律 静电场的概念 电场强度 ·电场强度叠加原理 电场强度的计算
复 习 • 电荷的量子化 • 电荷守恒定律 • 库仑定律 • 静电场的概念 • 电场强度 • 电场强度叠加原理 • 电场强度的计算
4-3 静电场的环路定理 静电场力所作的功 1、点电荷电场 点电荷q固定于原点0,试验电荷qo 在g的电场中由A点沿任意路径ACB 到达B点,取微元dl,电场力对qo的 元功为 dA=F.di=qE·dd E- 1 在点电荷的非匀强 4π6r2 电场中,电场力对 试验电荷所作的功 dA= 1_99or0.di= 1 qdo dr 4π6r1 4π62 与其移动时起始位 置与终了位置有关, 与其所经历的路径 A= 99o 4π ·dr= 4L60 无关
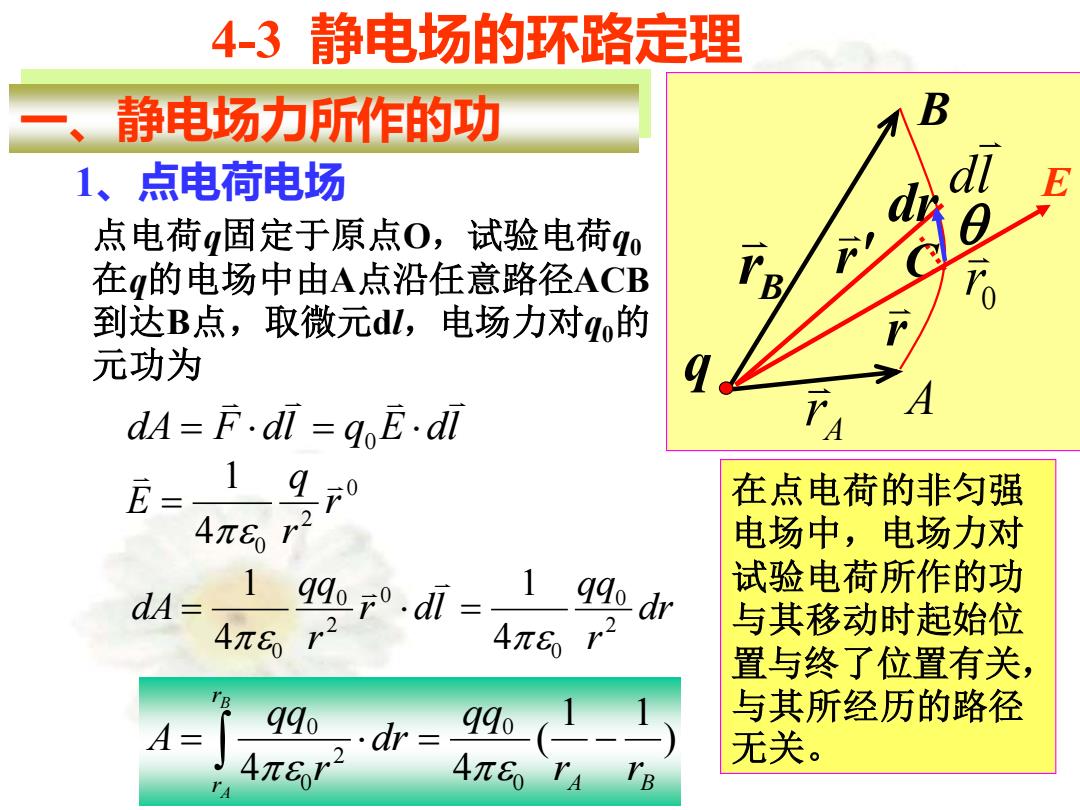
一、静电场力所作的功 4-3 静电场的环路定理 点电荷q固定于原点O,试验电荷q0 在q的电场中由A点沿任意路径ACB 到达B点,取微元dl,电场力对q0的 元功为 B r B A r A 1、点电荷电场 q C r r dr dl 0 r E dA F dl q E dl = = 0 0 2 4 0 1 r r q E = dr r qq r dl r qq dA 2 0 0 0 2 0 0 4 1 4 1 = = ) 1 1 ( 4 4 0 0 2 0 0 A B r r r r qq dr r qq A B A = = − 在点电荷的非匀强 电场中,电场力对 试验电荷所作的功 与其移动时起始位 置与终了位置有关, 与其所经历的路径 无关

2、任意带电体电场 任意带电体都可以看成由许多点电荷组成的点电荷系,根据 叠加原理可知,点电荷系的场强为各点电荷场强的叠加 E=E+E2+… 任意点电荷系的电场力所作的功为 A=9o∫Ei=9o∫E·i+9∫E,l+… 每一项均与路径无关,故它们的代数和也必然与路径无关。 3、结论 在真空中,一试验电荷在静电场中移动时,静电场力对它 所作的功,仅与试验电荷的电量、起始与终了位置有关, 而与试验电荷所经过的路径无关。 静电场力也是保守力,静电场是保守场
2、任意带电体电场 任意带电体都可以看成由许多点电荷组成的点电荷系,根据 叠加原理可知,点电荷系的场强为各点电荷场强的叠加 E = E1 + E2 + 任意点电荷系的电场力所作的功为 = = + + l l l A q E dl q E dl q E dl 0 0 1 0 2 每一项均与路径无关,故它们的代数和也必然与路径无关。 3、结论 在真空中,一试验电荷在静电场中移动时,静电场力对它 所作的功,仅与试验电荷的电量、起始与终了位置有关, 而与试验电荷所经过的路径无关。 静电场力也是保守力,静电场是保守场
二、静电场的环路定理 在静电场中,将试验电荷沿闭合路 径移到一周时,电场力所作的功为 A-ja.E-d-a.jE-dl A=go∫E.di+g6∫Edn 电场力作 ABC CDA 功 ∫E.dl=-∫Edn 与路径无 CDA ADC 关 9∫Edl=∫Edi 定义:电场强度沿任意闭合路径 ADO ABC 的线积分叫电场强度的环流。 A=qoE.dl=0 fE·dl=0 静电场环路定理:在静电场中, 电场强度的环流为零
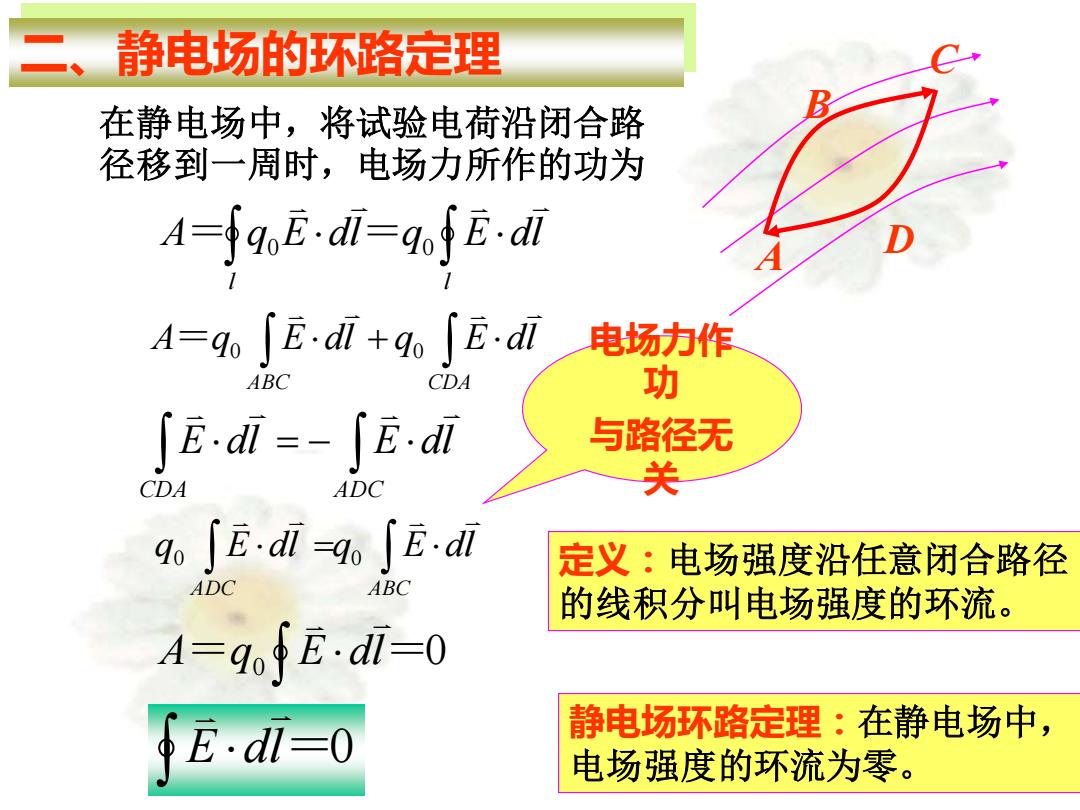
二、静电场的环路定理 在静电场中,将试验电荷沿闭合路 径移到一周时,电场力所作的功为 l l A q E dl q E dl = 0 = 0 A B C D + ABC CDA A q E dl q E dl = 0 0 = − CDA ADC E dl E dl = ADC ABC q E dl q E dl 0 0 = 0 =0 A q E dl =0 E dl 电场力作 功 与路径无 关 定义:电场强度沿任意闭合路径 的线积分叫电场强度的环流。 静电场环路定理:在静电场中, 电场强度的环流为零

三、电势能 电荷在电场的一定位置上,具 有一定的能量,叫做电势能。 静电场力对电荷所作的功等于电 势能增量的负值。 A,6=g6E.di=-(W。-Wa)=W。-W g心Ea=w。-w 电势能的参考点选择也是任意的,若W,=0,则电场中a 点的电势能为: 参考点 W。=qoJa E.dl 结论:试验电荷g在电场中点a的电 势能,在取值上等于把它从点a移 Wp=.di 到到零电势能处的电场力所作的功
三、电势能 电荷在电场的一定位置上,具 有一定的能量,叫做电势能。 a b 静电场力对电荷所作的功等于电 势能增量的负值。 b a a b b a Aab = q0 Edl = −(W −W ) =W −W a b b a q Edl =W −W 0 电势能的参考点选择也是任意的,若Wb=0,则电场中a 点的电势能为: = 参考点 a a W q E dl 0 结论:试验电荷q0在电场中点a的电 势能,在取值上等于把它从点a移 到到零电势能处的电场力所作的功。 = p p W q E dl 0

4-4电势 电势 1、电势 比值W/g与q无关,只决定于电场的性质及场点的位 置,所以这个比值是反映电场本身性质的物理量,可以 称之为电势 静电场中带电体所具有的电势能与该带电体的电 量的比值定义为电势 参考点 V。=W,1g=JD E.dl 当电荷分布在有限空 •电场中某点的电势在数值上等于放 间时,无限远处的电 在该点的单位正电荷的电势能 势能和电势为零 •电场中某点的电势在数值上等于把 =E.di 单位正电荷从该点移到势能为零的 p 点时,电场力所作的功
4-4 电 势 一、电势 1、电势 比值 Wp / q0与q0无关,只决定于电场的性质及场点的位 置,所以这个比值是反映电场本身性质的物理量,可以 称之为电势 静电场中带电体所具有的电势能与该带电体的电 量的比值定义为电势。 = = 参考点 p p p V W q E dl 0 / 当电荷分布在有限空 间时,无限远处的电 势能和电势为零 = p p V E dl •电场中某点的电势在数值上等于放 在该点的单位正电荷的电势能 •电场中某点的电势在数值上等于把 单位正电荷从该点移到势能为零的 点时,电场力所作的功

2、说明: •电势是标量,有正有负; 电势的单位:伏特1V=1JC1; •电势具有相对意义,它决定于电势零点的选择。在理论 计算中,通常选择无穷远处的电势为零; •在实际工作中,通常选择地面的电势为零。 但是对于“无限大”或“无限长”的带电体,只能在 有限的范围内选取某点为电势的零点。 3、电势差 在静电场中,任意两点A和点B之间的电 势之差,称为电势差,也叫电压。 Us='4-V。=∫E·l 静电场中任意两点A、B之间的电势差,在数值上等于 把单位正电荷从点A移到点B时,静电场力所作的功。 W=qo∫E·dl=qUAB=q(VA-Vs)
2、说明: •电势是标量,有正有负; •电势的单位:伏特1V=1J.C-1; •电势具有相对意义,它决定于电势零点的选择。在理论 计算中,通常选择无穷远处的电势为零; •在实际工作中,通常选择地面的电势为零。 •但是对于“无限大”或“无限长”的带电体,只能在 有限的范围内选取某点为电势的零点。 3、电势差 在静电场中,任意两点A和点B之间的电 势之差,称为电势差,也叫电压。 = − = AB AB A B U V V E dl 静电场中任意两点A、B之间的电势差,在数值上等于 把单位正电荷从点A移到点B时,静电场力所作的功。 ( ) AB A B B A W = q E dl = q U = q V −V 0 0 0
二、点电荷电场的电势 正电荷的电势为正,离电 v-jEa-了 荷越远,电势越低; 4元61 负电荷的电势为负,离电 荷越远,电势越高。 三、电势叠加原理 2 连续分布电荷电场的电势 1、点电荷系电场的电势 电场由几个点电 荷q1,42,n E=∑E 产生 v=∫Ei=∫∑E,dl =∑JE·i=∑ dq 点电荷系所激发的电场中 dy- dq_ 某点的电势,等于各点电 4元8' 荷单独存在时在该点的电 Adl 势的代数和。这个结论叫 线分布1 做静电场的电势叠加原理
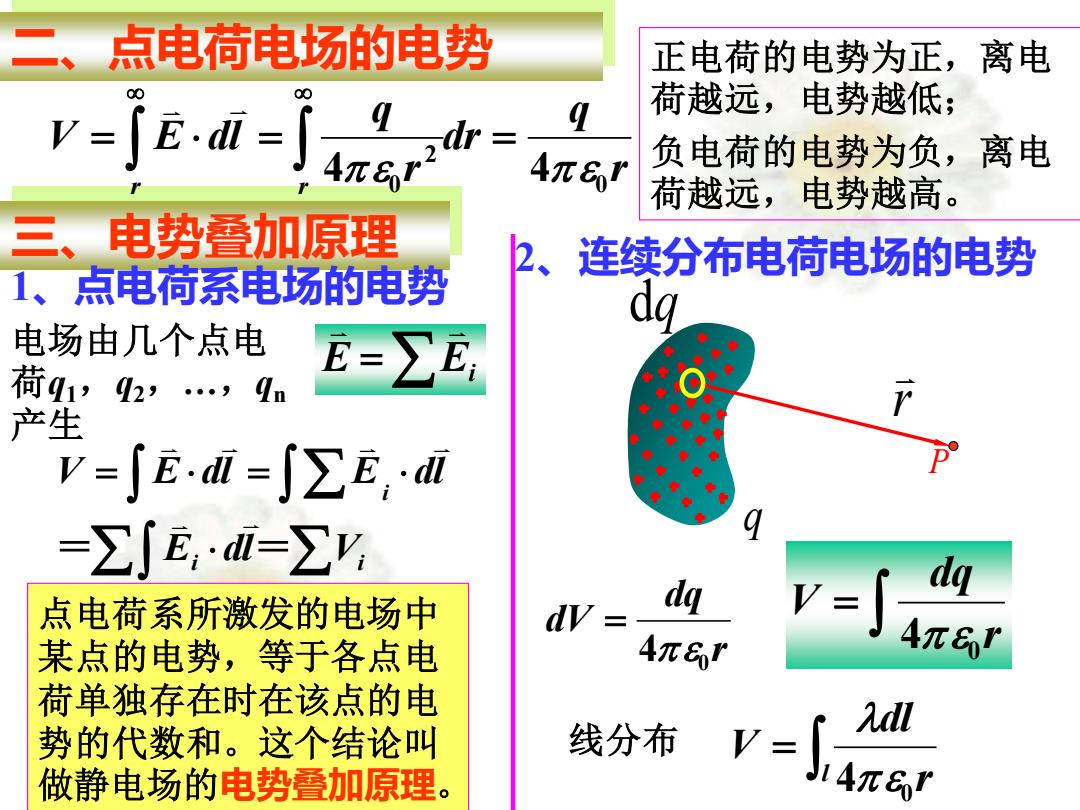
三、电势叠加原理 1、点电荷系电场的电势 电场由几个点电 荷q1,q2,…,qn 产生 E = Ei = = i i i E dl V V E dl E dl = = 点电荷系所激发的电场中 某点的电势,等于各点电 荷单独存在时在该点的电 势的代数和。这个结论叫 做静电场的电势叠加原理。 2、连续分布电荷电场的电势 r dq dV 4 0 = = r dq V 4 0 线分布 = l r dl V 4 0 二、点电荷电场的电势 r q dr r q V E dl r r 0 2 4 0 4 = = = 正电荷的电势为正,离电 荷越远,电势越低; 负电荷的电势为负,离电 荷越远,电势越高。 q r P dq

3、电势的计算 步骤: 计算电势的方法有两种: ()先算场强 利用电势的定义式 (2)选择合适的路径L 3)积分(计算) 要注意参考点的选择,只有电荷分布在有限的空间时, 才能选无穷远点的电势为零; 积分路径上的电场强度的函数形式要求己知或可求。 步骤 利用电势的叠加原理 (1)把带电体→分为无限多dq V= dq (2)由dq→dp 3)由d0→φ=∫d0 要求电荷的分布区域是已知的; 当电荷分布在有限的区域内,可以选择无穷远点作为 电势的零点的;而当激发电场的电荷分布延伸到无穷远 时,只能根据具体问题的性质,在场中选择某点为电势 的零点
3、电势的计算 计算电势的方法有两种: •利用电势的定义式 B AB VA = E dl +V 要注意参考点的选择,只有电荷分布在有限的空间时, 才能选无穷远点的电势为零; 积分路径上的电场强度的函数形式要求已知或可求。 •利用电势的叠加原理 = r dq V 4 0 要求电荷的分布区域是已知的; 当电荷分布在有限的区域内,可以选择无穷远点作为 电势的零点的;而当激发电场的电荷分布延伸到无穷远 时,只能根据具体问题的性质,在场中选择某点为电势 的零点。 步骤: (1)先算场强 (2)选择合适的路径L (3) 积分(计算) 步骤 (1)把带电体→分为无限多dq (2)由dq → d (3)由d → = d