
银川川大学栽学镖件 物理学电子教案 刚体转动的动能定理 1、力矩作功 2、刚体绕定轴转动的动能定理
物理学电子教案 银川大学教学课件 刚体转动的动能定理 1、力矩作功 2、刚体绕定轴转动的动能定理

1.力矩 M=rxF 其大小: M=FrsinO 其方向:由右手螺旋法则来确定。 2.转动定律 M=Ia 3.转动惯量 1=2am2I=j小wrdm i=1 如:半径为R、质量为的圆盘,转轴垂直于盘面且通过中心 R 2
1.力矩 其大小: 3.转动惯量 其方向:由右手螺旋法则来确定。 复习 2.转动定律 M r F = M Fr = sin M I = 2 1 n i i i I m r = = 2 M I r dm = 如:半径为R、质量为m的圆盘,转轴垂直于盘面且通过中心 1 2 2 I mR =

3~3刚体定轴转动的动能定理 本节,从功和能的角度来讨论刚体定轴转动的问题。 一、力矩作功 dA=F.dr=Fds Frde d4=Mde 即:外力对转动刚体所做的元功等于相应力矩和角位移的乘积
o z F Ft Fn Ft o r r d d t t d d d d A F r F s F r = = = d d A M= 本节,从功和能的角度来讨论刚体定轴转动的问题。 即:外力对转动刚体所做的元功等于相应力矩和角位移的乘积。 3-3 刚体定轴转动的动能定理 一、力矩作功

刚体从角坐标8,转到角坐标0 力矩的功 A= t 说明:力矩作功的实质仍然是力作功。对于刚体转动的情 况,用力矩的角位移来表示。 若有若干个外力作用于刚体上,合外力矩就等于外力 矩的代数和,此时得到的功就是合外力矩的功。 力矩的功率:表示力矩做功的快慢。 dA P- =M dt dt 即:力矩的瞬时功率等于力矩的大小与角速度大小的乘积
0 A Md = 力矩的功 刚体从角坐标 0 转到角坐标 力矩的功率:表示力矩做功的快慢。 dA d P M M dt dt = = = 即:力矩的瞬时功率等于力矩的大小与角速度大小的乘积。 若有若干个外力作用于刚体上,合外力矩就等于外力 矩的代数和,此时得到的功就是合外力矩的功。 说明:力矩作功的实质仍然是力作功。对于刚体转动的情 况,用力矩的角位移来表示

二、 刚体的转动动能 刚体以角速度o作定轴转动 质元 △m,距转轴一 ,速度为— V-r@ 动能为 整个刚体的动能就是各个质元的动能之和 E,=∑Ea=∑)Auo2=amrb2 用转动惯量表示 2 列体绕定轴转动的转动动能等于刚体的转动惯量与 角速度的平方的乘积的一半
二、刚体的转动动能 刚体以角速度ω作定轴转动 质元——Δmi,距转轴——ri,速度为——vi=riω 动能为 2 2 2 2 1 2 1 Eki = mi vi = mi ri 整个刚体的动能就是各个质元的动能之和 ( ) 2 2 2 2 2 1 2 1 Ek =Ek i = mi ri = mi ri 用转动惯量表示 2 2 1 Ek = I 刚体绕定轴转动的转动动能等于刚体的转动惯量与 角速度的平方的乘积的一半。 z o ri mi i v

三、刚体绕定轴转动的动能定理 设定轴转动的刚体在合外力矩M的作用下,刚体绕定轴转过的 角位移为d0,合外力矩对刚体所作的元功为 dA MdO dw M=Ia=I dt dA=I do=l@do dt dt 刚体绕定轴转动的动能 A=∫H=1jodo 定理:合外力矩对绕定 00 轴转动的刚体所作的功 等于刚体的转动动能的 A=102-1=E-E 增量
三、刚体绕定轴转动的动能定理 dA = Md d I d dt d d I dt d dA = I = = dt d M I I = = = 0 A= dA I d Ek Eko A I I = − 2 0 2 2 1 2 1 = - 刚体绕定轴转动的动能 定理:合外力矩对绕定 轴转动的刚体所作的功 等于刚体的转动动能的 增量。 设定轴转动的刚体在合外力矩M的作用下,刚体绕定轴转过的 角位移为 d ,合外力矩对刚体所作的元功为
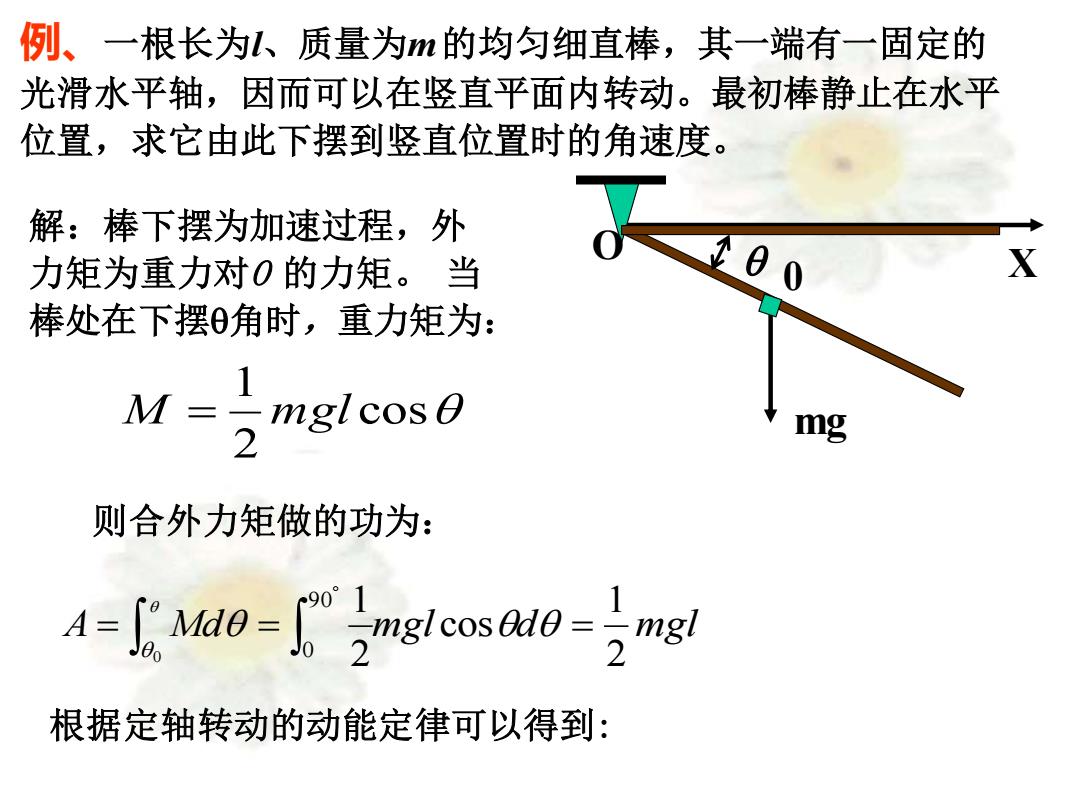
例、一根长为l、质量为m的均匀细直棒,其一端有一固定的 光滑水平轴,因而可以在竖直平面内转动。最初棒静止在水平 位置,求它由此下摆到竖直位置时的角速度。 解:棒下摆为加速过程,外 力矩为重力对0的力矩。当 00 X 棒处在下摆0角时,重力矩为: 1 M=mgl cos 2 mg 则合外力矩做的功为: AMdo-mleos-mg! 根据定轴转动的动能定律可以得到:
例、一根长为l、质量为m 的均匀细直棒,其一端有一固定的 光滑水平轴,因而可以在竖直平面内转动。最初棒静止在水平 位置,求它由此下摆到竖直位置时的角速度。 解:棒下摆为加速过程,外 力矩为重力对O 的力矩。 当 棒处在下摆角时,重力矩为: X O mg 0 cos 2 1 M = mgl A Md mgl d mgl 2 1 cos 2 9 0 1 0 0 = = = 根据定轴转动的动能定律可以得到: 则合外力矩做的功为:

mgl= 2 2-0 1 I= m2 3 得到: 0=1 3g 本题还可以用机械能守恒定律来解
0 2 1 2 1 2 mgl = I − 2 3 1 I = ml l 3g 得到: = 本题还可以用机械能守恒定律来解

例题35:如图所示,一质量为M、半径为R的圆盘,可绕一无摩 擦的水平轴转动。圆盘上绕有轻绳,一端悬挂质量为的物体。 问物体由静止下落高度时,其速度的大小为多少?设绳的质量 忽略不计。 解:圆盘和物体的受力如图,对于 圆盘,根据定轴转动的动能定律 TRAO=102-10 2 I-MR2 2 对于物体来说,由质点动能定理,得 2 2 D
例题3-5:如图所示,一质量为M、半径为R的圆盘,可绕一无摩 擦的水平轴转动。圆盘上绕有轻绳,一端悬挂质量为m的物体。 问物体由静止下落高度h时,其速度的大小为多少?设绳的质量 忽略不计。 解:圆盘和物体的受力如图,对于 圆盘,根据定轴转动的动能定律 2 2 0 2 1 2 1 TR = I − I 2 2 1 I= MR 对于物体来说,由质点动能定理,得 2 0 2 2 1 2 1 mgh −T'h = m v − m v T’ T P N’ P’

由牛第三定律 T=T 由于绳与圆盘之间无相对滑动,故有 h=R△O v=Ro 解上述方程,可得 m V三 2gh V(M/2)+m
由牛顿第三定律 T = T' 由于绳与圆盘之间无相对滑动,故有 v R h R = = 解上述方程,可得 ( ) gh M m m v 2 / 2 + =