
第6章平面电磁波 黄丘林 电子工程学院 西安电子科技大学
第6章 平面电磁波 黄丘林 电子工程学院 西安电子科技大学 1

本章提纲 。1理想介质中的均匀平面波 。2平面波的极化 。3有耗媒质中的均匀平面波 。4均匀平面波对平面分界面的垂直入射 。5均匀平面波对理想导体表面的斜入射 。6均匀平面波对理想介质表面的斜入射 2
本章提纲 1 理想介质中的均匀平面波 2 平面波的极化 3 有耗媒质中的均匀平面波 4 均匀平面波对平面分界面的垂直入射 5 均匀平面波对理想导体表面的斜入射 6 均匀平面波对理想介质表面的斜入射 2

1理想介质中的均匀平面波 交变电磁场具有波动性,电场和磁场(龙,庄)都满 足波动方程,其解是以波动的形式在空间传播的, 即电磁波。 ·平面波:波阵面是平面的波叫平面波。 均匀平面波:波阵面上各点电场E和磁场丑都分别 相等的平面波叫均匀平面波。 均匀平面波是一种理想模型,但实际中某些电磁波 可作为均匀平面波处理。如:偶极子天线的远区辐 射场是球面波,但当球面半径足够大,而研究其一 个局部时,可近似认为是均匀平面波。 3
1 理想介质中的均匀平面波 交变电磁场具有波动性,电场和磁场( , )都满 足波动方程,其解是以波动的形式在空间传播的, 即电磁波。 平面波:波阵面是平面的波叫平面波。 均匀平面波:波阵面上各点电场 和磁场 都分别 相等的平面波叫均匀平面波。 均匀平面波是一种理想模型,但实际中某些电磁波 可作为均匀平面波处理。如:偶极子天线的远区辐 射场是球面波,但当球面半径足够大,而研究其一 个局部时,可近似认为是均匀平面波。 E H E H 3

1理想介质中的均匀平面波 。均匀平面波方程 在均匀、线性、各向同性的理想介质中的无源区域, 复数形式的麦克斯韦方程组为: V×H=j08E V×E=-j0uH V.i=0 V.E=0 若均匀平面波是沿之轴方向传播的,测等相位面为2C 的平面,由均匀平面波的定义,E、i与x、y无关,即: =0 8x
1 理想介质中的均匀平面波 均匀平面波方程 在均匀、线性、各向同性的理想介质中的无源区域, 复数形式的麦克斯韦方程组为: 若均匀平面波是沿z轴方向传播的,则等相位面为z=C 的平面,由均匀平面波的定义, 、 与x、y无关,即: 0 0 H j E E j H H E = = − = = E H 0 x y = = 4

1理想介质中的均匀平面波 则: ax a, VxH= 00 H. H H a,+是马,=aa8a+ae) 0z .E=- 1 OH, 1( Hs E.=0 jos 0z jos 0z 5
1 理想介质中的均匀平面波 则: ∴ 0 0 x y z x y z a a a H z H H H = ( ) y x x y x x y y z z H H a a j a E a E a E z z = − + = + + 1 y x H E j z = − 1 x y H E j z = − 0 E z = 5

1理想介质中的均匀平面波 同理,由:V×E=-j0uH 得: 1 E H.=0 (*) jou oz jou dz 可见:理想介质中的均匀平面波是横电磁波或TEM 波,将坐标系旋转使x轴与彦方向一致,则电场只有 x分量,则: E=Eax 由(*),i只有y分量 1 OBsd, 6 jou oz
1 理想介质中的均匀平面波 同理,由: 得: 可见:理想介质中的均匀平面波是横电磁波或TEM 波,将坐标系旋转使x轴与 方向一致,则电场只有 x分量,则: 由(*), 只有y分量: = − E j H 1 y x E H j z = − 1 x y E H j z = − 0 H z = (*) E E E a = x x H 1 x y E H a j z = − 6

1理想介质中的均匀平面波 ·此时,均匀平面波只有配,、H,二分量。 E=- 整w恶】 jos oz 1a2E. 02u60z2 Es+kE,=0 dz2 其解为: E,=Aeik:+Beik= 7
1 理想介质中的均匀平面波 此时,均匀平面波只有 、 二分量。 ∴ 其解为: E x H y 1 1 1 y x x H E E j z j z j z = − = − − 2 2 2 1 E x z = − 2 2 2 0 x x d E k E d z + =jk z jk z E Ae B e x − = + 7

1理想介质中的均匀平面波 o 第一项代表沿+z方向传播的波,第二项代表沿-2方 向传播的波。 ·以+z方向传播的波为例讨论: E.Ae-ik= 则: E.= E 04 Es 7= 媒质的波阻抗(单位Ω) H 真空中:7=120π≈3772 8
1 理想介质中的均匀平面波 第一项代表沿+z方向传播的波,第二项代表沿-z方 向传播的波。 以+z方向传播的波为例讨论: 则: 真空中: jk z E Ae x − = ( ) 1 jk z x y x k E H A jk e E j − = − − = = x y E H = = ——媒质的波阻抗(单位Ω) 0 = 120 377 8

1理想介质中的均匀平面波 E=aEx H=a,H,=a×a a×E 7 7 龙.i=0 .∴均匀平面波的电场、磁场相互垂直,且垂直于传播 方向 实数 故,龙和庄同相 9
1 理想介质中的均匀平面波 ∴ 均匀平面波的电场、磁场相互垂直,且垂直于传播 方向 ∵ ——实数 故 , 和 同相 E a E = x x x 1 y y z x z E H a H a a a E = = = E H = 0 x y E H = E H 9
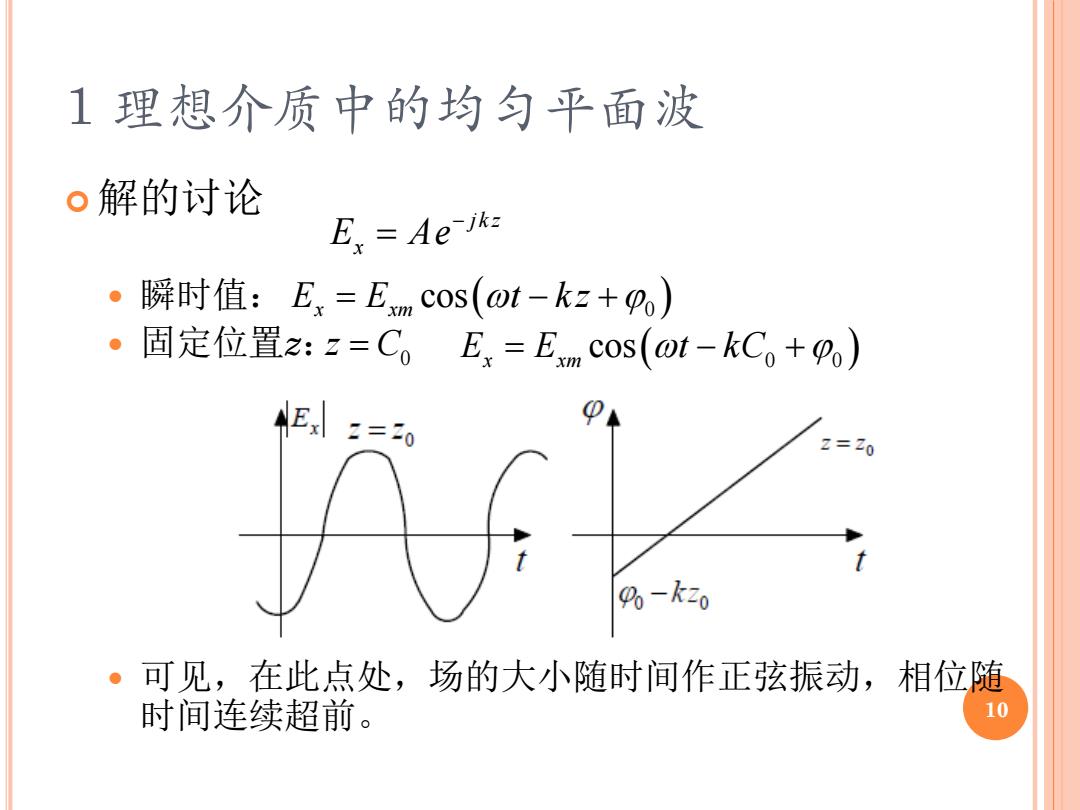
1理想介质中的均匀平面波 。解的讨论 E.Ae-ik= ·瞬时值:Ex=Em cos(ot-kz+) ·固定位置2:z=CE,=E coS(ot-kC+g) Ex=0 z=20 %6-k20 ·可见,在此点处,场的大小随时间作正弦振动,相位随 时间连续超前。 10
解的讨论 瞬时值: 固定位置z: 可见,在此点处,场的大小随时间作正弦振动,相位随 时间连续超前。 1 理想介质中的均匀平面波 jk z E Ae x − = E E t k z x xm = − + cos( 0 ) 0 z C= E E t kC x xm = − + cos( 0 0 ) 10