
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第十讲:矩方法
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第十讲:矩方法

本讲要点 口矩的几种定义 口简单的矩方法 口一般的矩方法 口矩方法与最大似然法和最小二乘法的比较 2
2 本讲要点 矩的几种定义 简单的矩方法 一般的矩方法 矩方法与最大似然法和最小二乘法的比较

自旋宇称在实验中的确定问题 实验上通常观测的是几种态的叠加,需要用几方面的实验观测来区分各 种可能的自旋取值以及相应分布范围,例如 J/Ψ→y+X,X→K++K 80 (AaW sz)/siuan3 0 Jw→YKK 注意:X可以包含有几个粒子 (如左图)。 60 已知:与自旋宇称有关的概率 50 不可能从质量范围来 密度函数包含三个实验观测角 40 定义单的粒子态! 度和一个不变质量。 30 问题:能否存在一种简单而又 不失精确度的方法确定自旋? 名 f3(1525) X(1710) 矩方法。 0 .21.31.41.51.61.71.81.9 2 M(KK)(GeV) 3
3 自旋宇称在实验中的确定问题 + − J / Ψ → γ + X, X → K + K 注意:X 可以包含有几个粒子 (如左图 )。 已知:与自旋宇称有关的概率 密度函数包含三个实验观测角 度和一个不变质量。 问题:能否存在一种简单而又 不失精确度的方法确定自旋? (1525) ' 2f X (1710) 实验上通常观测的是几种态的叠加,需要用几方面的实验观测来区分各 种可能的自旋取值以及相应分布范围,例如 矩方法。 不可能从质量范围来 定义单一的粒子态!

概率分布中的矩定义 考虑一个服从概率密度函数P(x)的连续随机变量x。 定义围绕一 固定值x,的第k阶矩或简单矩为 L=(x-xo)*P(x)dx 代数矩 4=∫x*P(x)d 如果令xo=0,则一阶矩就是随机变量x的期待值定义(也称作一阶代数矩) Ex]=∫xP(x)a=4=4 如果令xo=E[x],随机变量x围绕期待值的二阶矩就是随机变量x的方差 定义(也称作二阶中心矩) V[x]=J(x-E[x])'P(x)d=o2=4, 4
4 概率分布中的矩定义 ∫ = x − x P x dx k k ( ) ( ) μ 0 如果令 x 0=0,则一阶矩就是随机变量 x 的期待值定义 (也称作一阶代数矩 ) 1 [ ] = ( ) = μ = μ′ ∫ E x xP x dx 如果令 x 0 =E[x] , 随机变量 x 围绕期待值的二阶矩就是随机变量 x 的方差 定义 (也称作二阶中心矩 ) 2 2 2 [ ] = ( − [ ]) ( ) = σ = μ ∫ V x x E x P x dx 代数矩 ∫ ′ = x P x dx k k μ ( ) 0 P x( ) x x k 考虑一个服从概率密度函数 的连续随机变量 。定义围绕一 固定值 的第 阶 矩 或简单矩 为

代数矩与中心矩的关系 代数矩 中心矩 6=1 低阶矩之间的 40=1 4=4 关系 4=0 =o2+u2 42=巧-2 42=02 般情况下,它们的关系可以有如下表示 口高阶矩对研究概率密度函数在 x-u大值区间的行为很有帮助。 .u 口对称分布的所有奇数中心矩为 4=】 零。 5
5 代数矩与中心矩的关系 代数矩 中心矩 2 2 2 1 0 1 μ σ μ μ μ μ ′ = + ′ = ′ = 2 2 1 0 0 1 μ σ μ μ = = = 2 μ2 = μ2 ′ − μ 低阶矩之间的 关系 一般情况下,它们的关系可以有如下表示 l k l k l k k l l k k l l k l k ( ) ( ) 1 0 0 1 μ μ μ μ μ μ ′ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ′ = ′ − ′ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = − = = − ∑ ∑ 高阶矩对研究概率密度函数在 |x - μ|大值区间的行为很有帮助。 对称分布的所有奇数中心矩为 零。 高阶矩对研究概率密度函数在 |x - μ|大值区间的行为很有帮助。 对称分布的所有奇数中心矩为 零
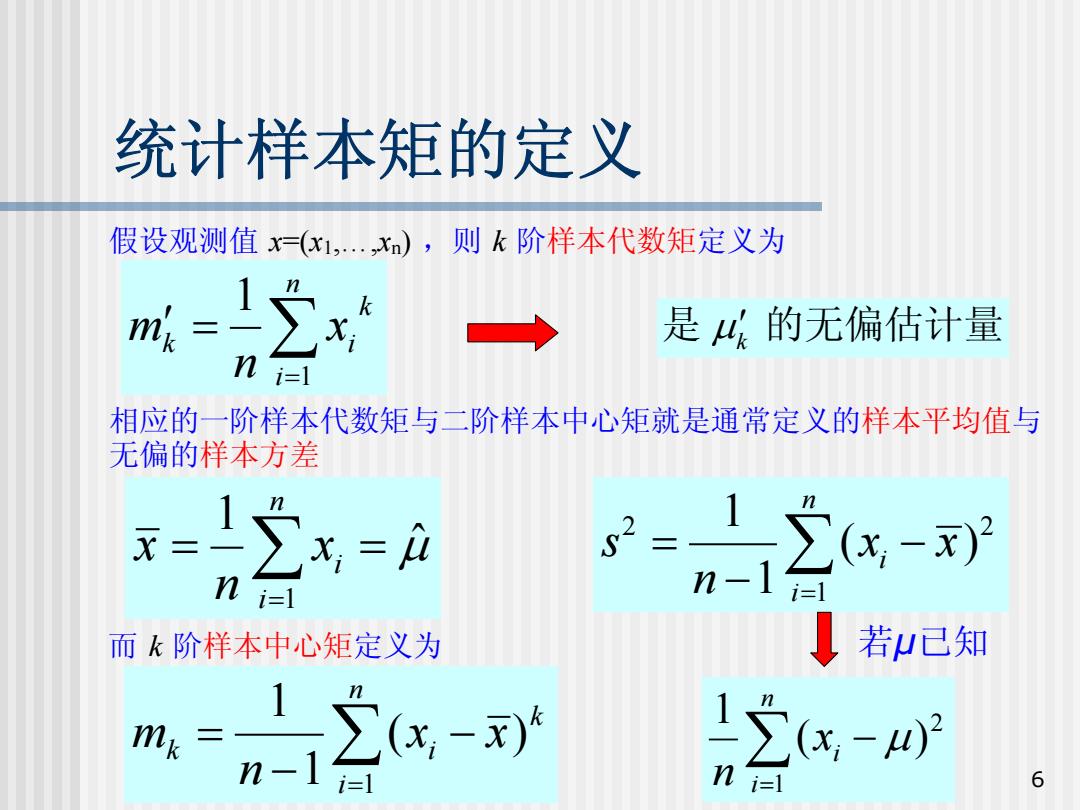
统计样本矩的定义 假设观测值=(x1,…x),则k阶样本代数矩定义为 m=1x 是4(的无偏估计量 n i=1 相应的一阶样本代数矩与二阶样本中心矩就是通常定义的样本平均值与 无偏的样本方差 x= x,=i 2= n i=1 .- 而k阶样本中心矩定义为 若已知 mk 2x- ;1 n i=1 6
6 统计样本矩的定义 假设观测值 x=(x1,…, x n ) ,则 k 阶样本代数矩定义为 相应的一阶样本代数矩与二阶样本中心矩就是通常定义的样本平均值 与 无偏的样本方差 μˆ 1 1 = ∑ = = n i i x n x ∑= ′ = n i k k i x n m 1 1 2 2 1 1 ( ) 1 n i i s x x n = = − − ∑ 而 k 阶样本中心矩定义为 ∑= − − = n i k k i x x n m 1 ( ) 1 1 若 µ已知 ∑= − n i i x n 1 2 ( ) 1 μ μk 是 ′ 的无偏估计量

用简单矩方法测定待定参数 考虑采用计算随机变量x自身代数矩的简单方法,对含有r个参数 产=(2,.·,2)的概率密度函数情况,可以通过使r个不同阶代数矩 与对应的样本矩相等,建立方程组 4(元)=m r个方程 解出待定参数入 r个未知数 4(元)=m 可以证明样本矩的协方差矩阵为 =com0m-不. 参数的误差 7
7 用简单矩方法测定待定参数 r m r m ′ = ′ ′ = ′ ( ) ( ) 1 1 μ λ μ λ G # G r 个方程 r 个未知数 λ G 解出待定参数 可以证明样本矩的协方差矩阵为 ( ) 1 1 cov( , ) k l k l kl k l x x x n V m m − ⋅ − = ′ ′ ≅ + 参数的误差 1 ( r x r r r = λ λ G ,..., 考虑采用计算随机变量 自身代数矩的简单方法,对含有 个参数 的概率密度函数情况,可以通过使 个不同阶代数矩 与对应的样本矩相等,建 ) 立方程组
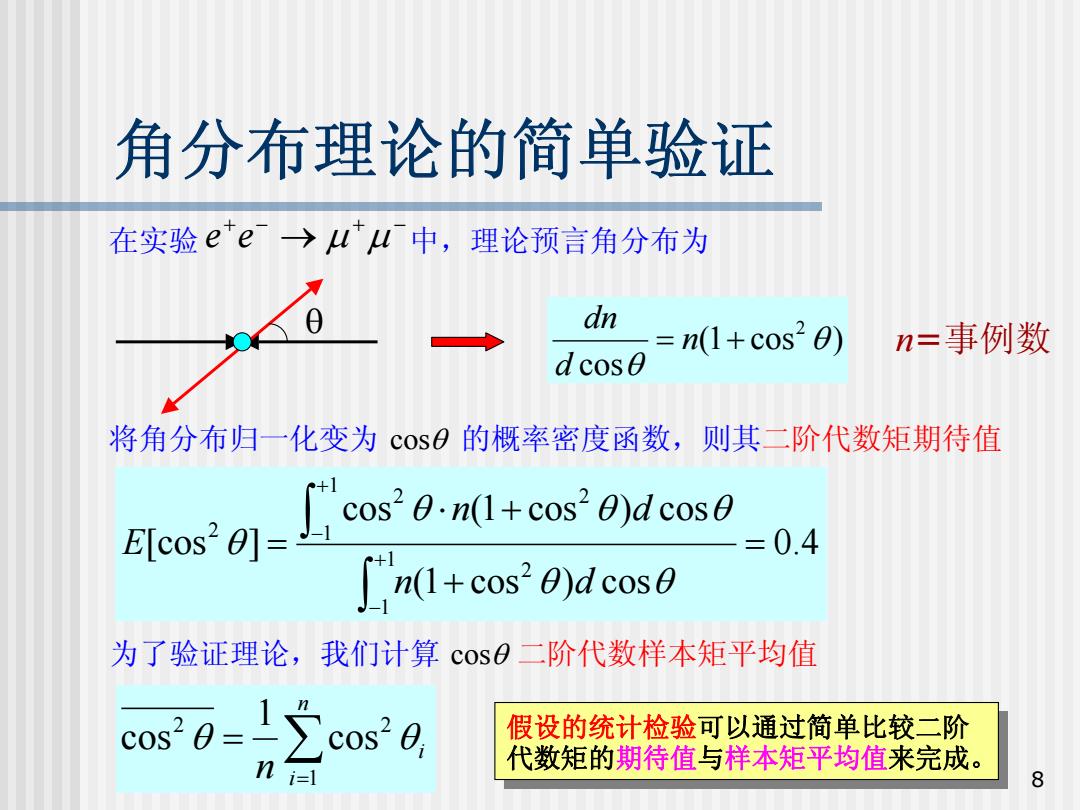
角分布理论的简单验证 在实验ee→u中,理论预言角分布为 dn n(1+cos20) n=事例数 dcos0 将角分布归一化变为cos0的概率密度函数,则其二阶代数矩期待值 E[cos2 01= con(1+cos0)dcos =0.4 n(1+cos20)d cos 为了验证理论,我们计算 cos0二阶代数样本矩平均值 c0s26=2c0s20 假设的统计检验可以通过简单比较二阶 n 代数矩的期待值与样本矩平均值来完成。 8
8 角分布理论的简单验证 在实验 中,理论预言角分布为 + − → + − e e μ μ 将角分布归一化变为 cos θ 的概率密度函数,则其二阶代数矩期待值 θ ( 1 cos ) cos 2 θ θ = n + d dn n =事例数 为了验证理论,我们计算 cos θ 二阶代数样本矩平均值 0.4 ( 1 cos ) cos cos ( 1 cos ) cos [cos ] 1 1 2 2 1 1 2 2 = + ⋅ + = ∫ ∫ + − + − θ θ θ θ θ θ n d n d E ∑= = n i i n 1 2 2 cos 1 cos θ θ 假设的统计检验可以通过简单比较二阶 代数矩的期待值与样本矩平均值来完成。 假设的统计检验可以通过简单比较二阶 代数矩的期待值 与样本矩平均值来完成

简单验证中的误差估计 在前面例子中对于不含参数的简单情形cos0二阶代数矩平均值的误差估 计可以按下列方法进行 已知真值 E[cos20]=0.4 样本矩的方差为 S2 =>(cos2e,-EIcos21)? i= 样本矩平均值的方差可以证明为 V[cos2θ]=S21n 假设实验观测1000次,c0s20=0.39,并计算出S2=0.15,则实验结果报告为 0.39士0.01观测值在一个标准误差范围内与理论预期相符。 9
9 简单验证中的误差估计 在前面例子中对于不含参数的简单情形 cos θ 二阶代数矩平均值的误差估 计可以按下列方法进行 [cos ] 0.4 2 已知真值 E θ = 样本矩的方差为 ∑= = − n i i E n S 1 2 2 2 2 (cos [cos ]) 1 θ θ 样本矩平均值的方差可以证明为 V [cos ] S / n 2 2 θ = 0.39 ±0.01 观测值在一个标准误差范围内与理论预期相符。 2 1000 θ = = 0.39, S 0.1 5, 假设实验观测 次,cos 2 并计算出 则实验结果报告为

含参数情况举例 在上例中,假设已知理论中包含一未知参数0,例如 dn n(1+acos2θ) d cos0 和前例一样,计算出cos0二阶代数矩的理论期待值 Elcos2 0]= cos20-n1+acos29dcos0 5+3 n(1+a cos20)d cos0 5(3+a) 则参数与二阶代数矩的关系为 5(3E[cos0]-1) a= 5(3cos20-1) 3-5E[cos20] 3-5cos20 只要函数是可积的,采用矩方法原则上就可以测定参数。 10
10 含参数情况举例 在上例中,假设已知理论中包含一未知参数 α,例如 和前例一样,计算出 cos θ 二阶代数矩的理论期待值 ( 1 cos ) cos 2 α θ θ = n + d dn 5 ( 3 ) 5 3 ( 1 cos ) cos cos ( 1 cos ) cos [cos ] 1 1 2 2 1 1 2 2 α α α θ θ θ α θ θ θ + + = + ⋅ + = ∫ ∫ + − + − n d n d E 3 5 [cos ] 5 ( 3 [cos ] 1 ) 2 2 θ θ α E E − − = 则参数 α与二阶代数矩的关系为 θ θ α 2 2 3 5cos 5 ( 3cos 1 ) ˆ − − = 只要函数是可积的,采用矩方法原则上就可以测定参数。 只要函数是可积的,采用矩方法原则上就可以测定参数