
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第二讲:常用概率密度函数
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第二讲 :常用概率密度函数

本讲要点 口常用的概率密度函数分布的数学形式 ▣相应的平均值与方差 口相关的应用范围
本讲要点 常用的概率密度函数分布的数学形式 相应的平均值与方差 相关的应用范围

二项式分布 N次独立测量,每次只有成功 可以证明其满足 (概率为p)或失败(概率为1-p) 归一化条件 两种可能。得到次成功的概率 N! 为 ∑”pu- N! P(r)= H(W-2P'(I-p)- =[1-p)+p]N=1 方差: 平均值: V[r]=o2 E[r]=4=∑rP(r)=Np =E[(r-4)2] 适用于仪器探 =E[r2]-E2[r] 测效率的计算 Np(1-p)
二项式分布 N 次独立测量,每次只有成功 (概率为 p)或失败(概率为1- p) 两种可能。得到 r次成功的概率 为 r N r p p r N r N P r − − − = ( 1 ) !( )! ! ( ) E [ r ] = = ∑rP ( r ) = Np : μ 平均值 ( 1 ) [ ] [ ] [( ) ] [ ] : 2 2 2 2 Np p E r E r E r V r = − = − = − = μ σ 方差 适用于仪器探 测效率的计算 适用于仪器探 测效率的计算 可以证明其满足 归一化条件 [( 1 ) ] 1 ( 1 ) !( )! ! = − + = − − ∑ − N r r N r p p p p r N r N
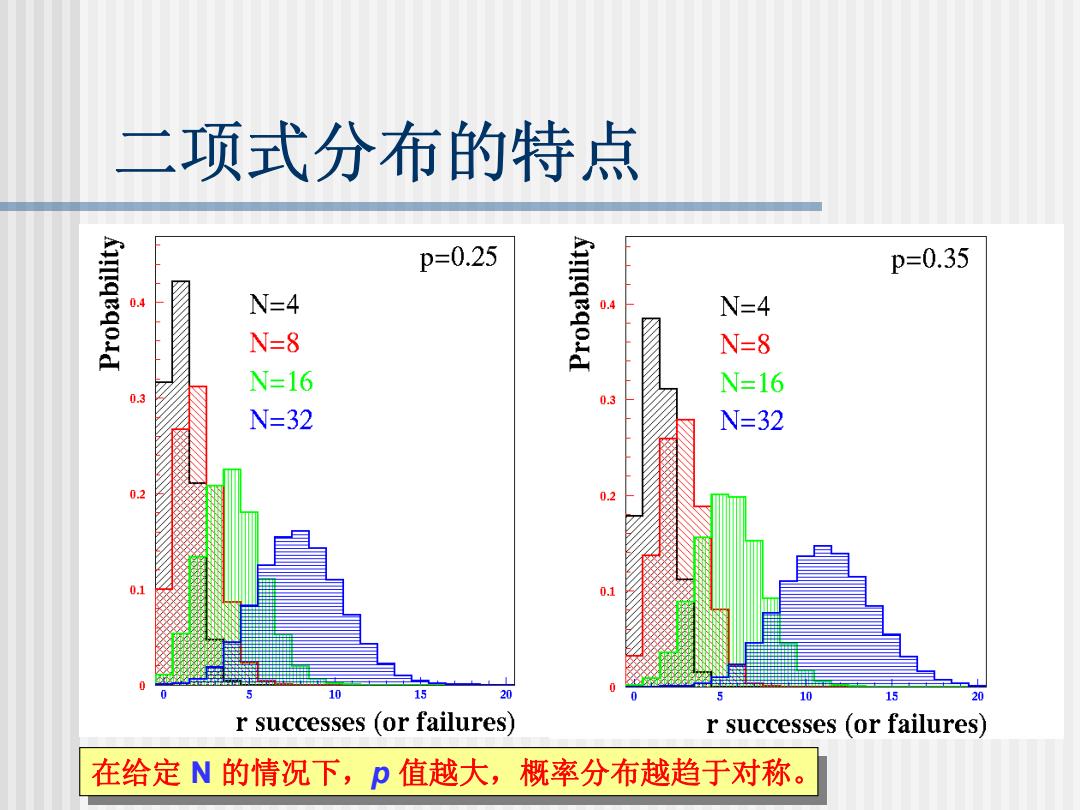
二项式分布的特点 Au!qeqoId p=0.25 p=0.35 0.4 N=4 0.4 N=4 N=8 A!qeqoId N=8 N=-16 N=16 0.3 0.3 N=32 N=32 0.2 0.1 10 15 20 公 r successes (or failures) r successes (or failures) 在给定N的情况下,p值越大,概率分布越趋于对称
二项式分布的特点 在给定 在给定 NN的情况下, 的情况下, pp值越大,概率分布越趋于对称。 值越大,概率分布越趋于对称
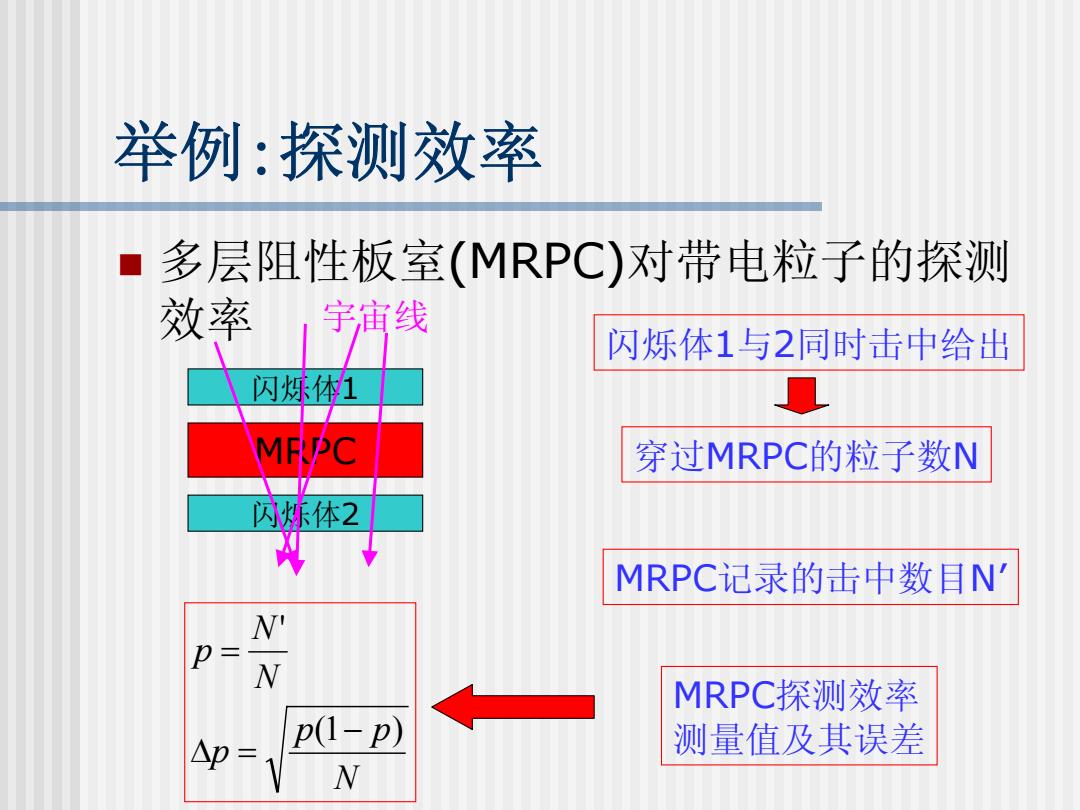
举例:探测效率 多层阻性板室(MRPC)对带电粒子的探测 效率 ,宇庙线 闪烁体1与2同时击中给出 闪烁体1 穿过MRPC的粒子数N 体2 MRPC记录的击中数目N' N p N MRPC探测效率 p(1-p) Ap= 测量值及其误差 N
举例:探测效率 多层阻性板室(MRPC)对带电粒子的探测 效率 闪烁体 1 MRPC 宇宙线 闪烁体 2 闪烁体 1 与 2同时击中给出 穿过MRPC的粒子数 N MRPC记录的击中数目N’ MRPC探测效率 测量值及其误差 N p p p N N p ( 1 ) ' − Δ = =

从二项式到多项式分布 类似于二项式分布,但允许结果的可能性m大于两种,概率为 p=(p1,p2,pm) 尝试N次,结果为 可能性1:n1 ∑p=1 →n=(n1,n2,,nm) 可能性2:n2 得到(n1,n2,,n)概率为 N! f(n)= nng.n p"p…p 平均值:[n,]=p, 方差:V[n,]=Np,(1-p) 适用于直方图 协方差:',=-Np,P,(i≠j) 频数误差估计
从二项式到多项式分布 类似于二项式分布,但允许结果的可能性m大于两种,概率为 1 ( , ..., ) 1 1 2 = = ∑= m i i m p p p p p G 尝试 N次,结果为 可能性 1:n 1 可能性 2:n 2 … ( , ,..., ) 1 2 m n = n n n G 得到(n 1,n 2,…,n m)概率为 1 2 3 ... ! !... ! ! ( ) 1 2 1 2 n m n n m p p p n n n N f n = G i Npi 平均值: E [ n ] = : [ ] ( 1 ) i i i 方差 V n = Np − p :V Np p ( i j ) 协方差 ij = − i j ≠ 适用于直方图 频数误差估计。 适用于直方图 频数误差估计
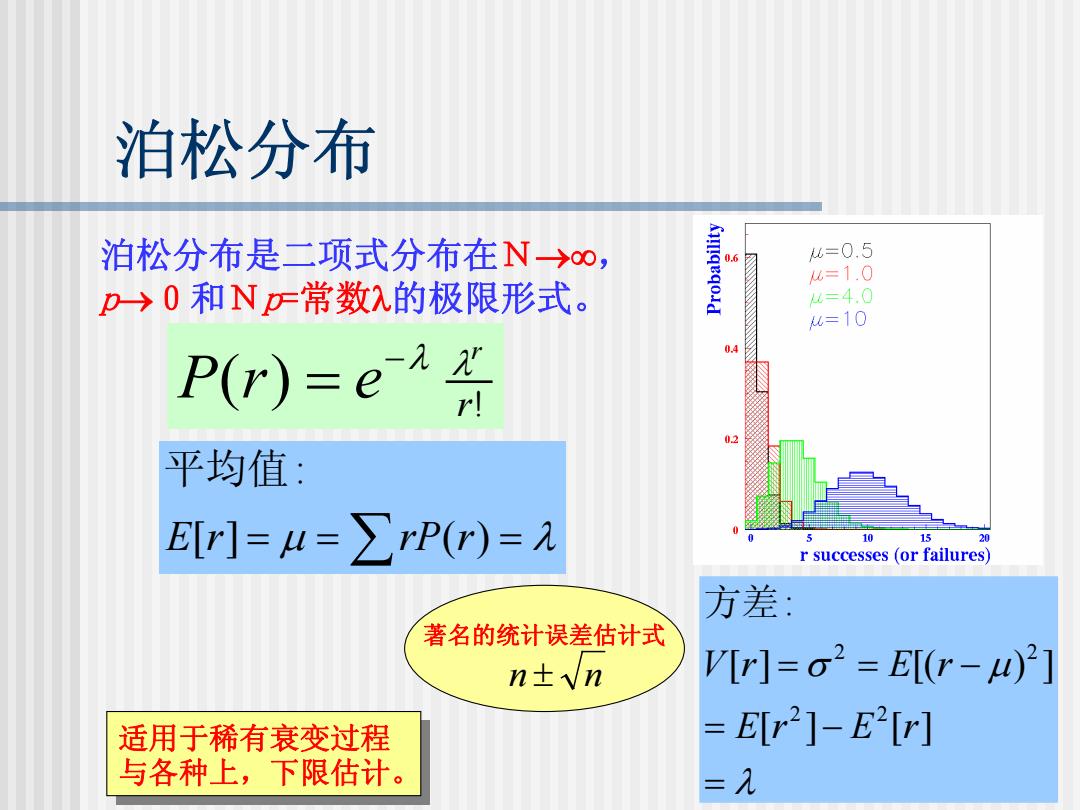
泊松分布 泊松分布是二项式分布在N→o, 0.6 6=0.5 =1.0 p→0和NF常数入的极限形式。 u=4.0 =10 P(r)=e 02 平均值: E[r]=u=∑rP()=元 0 15 20 r successes (or failures) 方差: 著名的统计误差估计式 n±Wn V[r]=o2=E(r-4)2] 适用于稀有衰变过程 =E[2]-E2[r] 与各种上,下限估计。 =见
泊松分布 泊松分布是二项式分布在N→∞, p→0和Np=常数λ的极限形式。 ! ( ) rr P r e−λ λ = [ ] = μ = ∑ ( ) = λ : E r rP r 平均值 2 2 2 2 : [ ] [( ) ] [ ] [ ] V r E r E r E r σ μ λ = = − = − = 方差 适用于稀有衰变过程 与各种上,下限估计。 适用于稀有衰变过程 与各种上,下限估计。 著名的统计误差估计式 n ± n

举例:光电倍增管暗电流影响 在有11146根PMT的探测 器中,已知每根PMT暗电 流产生的误击中为3.5kHz。 求探测器在任意总长度为 500us时间段观察到每隔 10 ns PMT误击中数目分 别为5和6的总次数 在10ns间隔观测到PMT误 日本超级神冈中微子探测器 击中的平均数目为 500μs =5→5×104× 0.45 ×e0.4三3(次) 10-8×11146×3500 5! =0.4 平均数 =6→5×104 0.46 ×e04=0.2(次) 61
举例:光电倍增管暗电流影响 在有11146 根PMT的探测 器中,已知每根PMT暗电 流产生的误击中为3.5kHz 。 求探测器在任意总长度为 500 μ s时间段观察到每隔 10ns PMT误击中数目分 别为 5 和 6的总次数 0.2 ( 次 ) 6! 0.4 6 5 10 3 ( 次 ) 5! 0.4 5 5 10 0.4 6 4 0.4 5 4 = ⇒ × × × ≅ = ⇒ × × × ≅ − − e e 在10ns间隔观测到PMT 误 击中的平均数目为 8 10 11146 3500 0.4 − × × = 500 μ s 平均数 日本超级神冈中微子探测器

二项式分布与泊松分布 假设一学生站在路边想搭便车。过路的汽车平均 频率为每分钟一辆,服从泊松分布。而每辆车让 搭便车的概率为1%,计算该学生在过了60辆车 以后还未能搭上车的可能性 N=60,p=0.01,r=0 特点:N大p小 601 根据二项式分布: 0.01°(1-0.01)60-00.5472 01(60-0)1 根据泊松分布:e60xo.o1 (60×0.01) 0.5488 01 泊松分布是二项式分布的近似
二项式分布与泊松分布 假设一学生站在路边想搭便车。过路的汽车平均 频率为每分钟一辆,服从泊松分布。而每辆车让 搭便车的概率为1%,计算该学生在过了60辆车 以后还未能搭上车的可能性 N=60, p=0.01,r=0 0.01 ( 1 0.01 ) 0.5472 0!(60 0)! 60! : 0 60 0 − = − 根据二 项式分布 − 0.5488 0! (60 0.01 ) : 0 60 0.01 = − × × 根据泊松分布 e 泊松分布是二项式分布的近似。 泊松分布是二项式分布的近似。 特点: N 大 p 小

泊松分布是二项式分布的近似 N=10 0.3 例如:对于以平均值为2 W=20 的泊松分布而言,相当于 N=50 二灯 项式分布中的Np=2。 W=100 0.2 当N值增大时,为了保持 泊松分布 Np不变,p值相应减小。 可以从右图看出,当N大 于50时,两种分布的区 0 别几乎可以忽略。 LLLL, 01 2345678910 r successes (or failures)
泊松分布是二项式分布的近似 例如:对于以平均值为 2 的泊松分布而言,相当于 二项式分布中的Np=2 。 当 N值增大时,为了保持 N p不变, p值相应减小。 可以从右图看出,当 N 大 于50时,两种分布的区 别几乎可以忽略。 r successes (or f ailures) Probability N=10 N=20 N=50 N=100 泊松分布