
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第十一讲:置信区间
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第十一讲:置信区间

本讲要点 统计误差中的标准误差问题 经典置信区间问题 ■利用似然函数或二乘函数确定置信区间 2
2 本讲要点 统计误差中的标准误差问题 经典置信区间问题 利用似然函数或二乘函数确定置信区间

测量结果的表述与含义 实验数据:x,,X 实验目的:估计日 并且还应给出6的方差,即o房。 结果应该报告成下述形式 0b±66=5.73±021 其真正的含义是什么呢? 如果我们知道0将服从某一概率密度函数分布g(0,O),那么上述 结果的正确表述应该是 0的估计值为5.73 的估计值为0.21 → o,测量了g(0,0)的分布宽度 3
3 测量结果的表述与含义 其真正的含义是什么呢? 1,..., n 实验数据:x x ˆ 实验目的:估计 θobs ˆ 5.73 0.21 ˆ ± ˆ = ± θ θ obs σ ˆ ˆ 如果我们知道 θ θ (; 将服从某一概率密度函数分布 g θ ),那么上述 结果的正确表述应该是 θ 的估计值为 5.73 ˆ 0.21 θ σ 的估计值为 m2 ˆ ˆ θ 并且还应给出 θ σ 的方差,即 。结果应该报告成下述形式 ˆ ˆ g( ; ) θ σ θ 测量了 θ 的分布宽度

参数估计值的分布 通常参数估计值服从的概率密度分布函数g(0;)是多维高斯分布 6和=cov©,0,]综合了我们对g(0,0)的了解或估计 可以用来作误差传递的输入参量, 以及用最小二乘法求平均值等等。 我们可以此约定来报告误差,而不管概率密度函数g(0:)的形式。 唯一例外的是当我们要对不同实验求平均值时,它的形式就会发挥作用。 如果g(0,)是高斯形式的话,置信区间可以表述为 [0b-6,0s+6a] 给出了对应于68.3%置信区间范围。 如果g(0:0)不是服从高斯分布 中心置信区间应给出不对称的误差 4
4 参数估计值的分布 ˆ 通常参数估计值服从的概率密度分布函数 g( ; θ θ ) 是多维高斯分布 ˆ ˆ ˆ m ˆ ˆ co v[ , ] ( ; ) θ θ V g = i j θ θ θ G G G 和 综合了我们对 的了解或估计 可以用来作误差传递的输入参量, 以及用最小二乘法求平均值等等。 ˆ 如果 g( ; θ θ ) 是高斯形式的话,置信区间可以表述为 ˆ ] ˆ ˆ , ˆ [ ˆ ˆ θ θ θ obs − σ θ obs + σ 中心置信区间应给出不对称的误差 ˆ 如果 g( ; θ θ ) 不是服从高斯分布 ˆ 我们可以此约定来报告误差,而不管概率密度函数 (g θ θ; ) 的形式。 唯一例外的是当我们要对不同实验求平均值时,它的形式就会发挥作用。 给出了对应于 68.3% 置信区间范围
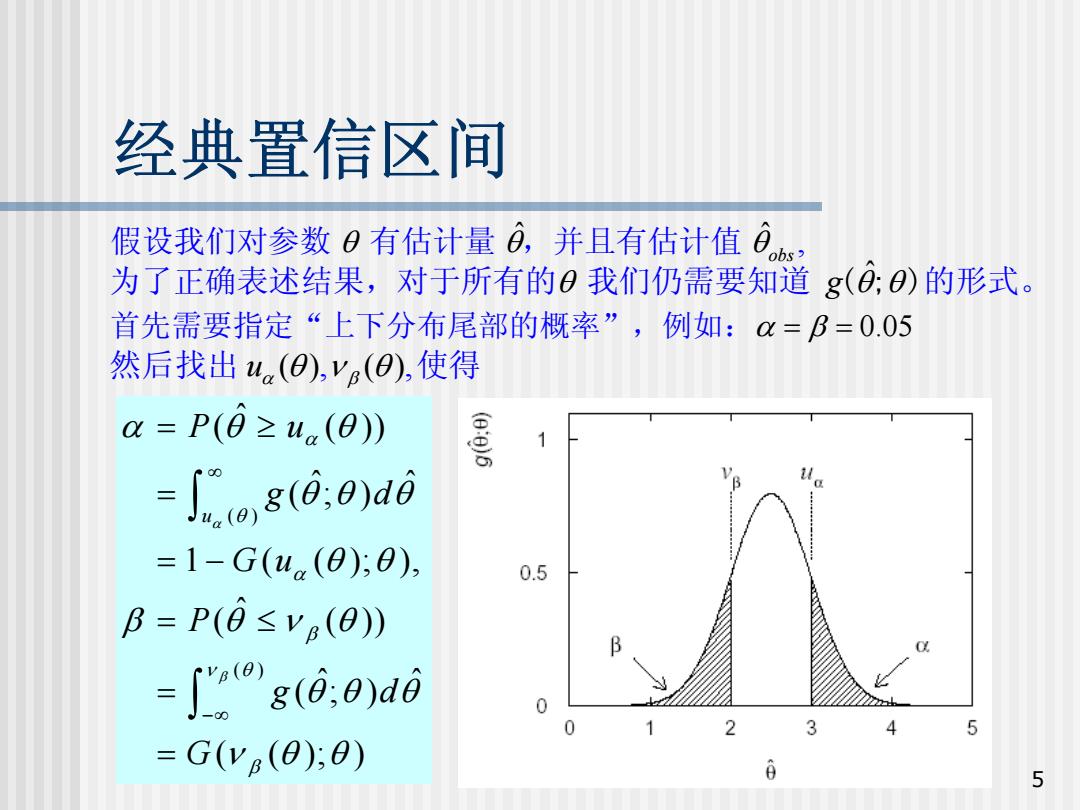
经典置信区间 假设我们对参数0有估计量日,并且有估计值 obs> 为了正确表述结果,对于所有的0我们仍需要知道g(0:O)的形式。 首先需要指定“上下分布尾部的概率”,例如:=B=0.05 然后找出4.(O),ye(0),使得 a=P(0≥ua(0) (e:e)6 o,8(d,e)d0 =1-G(u,(0);8) 0.5 B=P(0≤VB(0) B 」g(dodd =G(ye(0);0) 5
5 经典置信区间 首先需要指定“上下分布尾部的概率”,例如: α = β = 0.05 ( ) ( ) ˆ ( ( ) ) ˆ ˆ ( ; ) 1 ( ( ); ), ˆ ( ( ) ) ˆ ˆ ( ; ) ( ( ); ) u P u g d G u P g d G α β α θ α β ν θ β α θ θ θ θ θ θ θ β θ ν θ θ θ θ ν θ θ ∞ −∞ = ≥ = = − = ≤ = = ∫ ∫ ˆ ˆ , 假设我们对参数 θ 有估计量 θ θ ,并且有估计值 obs ˆ 为了正确表述结果,对于所有的θ θ 我们 仍需要知道 g( ; θ )的形式。 , u ( ) ( ), 然后找出 α β θ ν θ 使得

经典置信区间(续一) 无论0为何值,在置信带找到0的概率为。 P(ye(0)≤0≤u(0》=1-a-B 3 假设u(0),Ye(O)是单调变化的,那么 b (9) a(0)≡u(0),b(0)≡vg(⊙ 不等式 a 0≥u.(0),0≤vp(0) 3 等价于 在4.(0),v(O)之间的区域称为置信带 a(⊙)≥0,b(⊙)≤0→P(a(⊙≥0)=a,P(b(⊙≤0)=B 或者合并成 在不知道真值0的情况下,通过估计 P(a(0≤0≤b(0)=1-a-阝 值与函数a,b给出0的置信区间。 6
6 经典置信区间 (续一 ) 不等式 或者合并成 ˆ 无论θ θ 为何值,在置信带找到 的概率为 ˆ P v( ( ) u ( ) ) 1 β β θ ≤ ≤ θ θ = − α − β () u v, ( ) 假设 α β θ θ 是单调变化的,那么 1 1 ˆ ˆ ˆ ˆ a u ( ) ( ), b v ( ) ( ) θ α β θ θ θ − − ≡ ≡ ˆ ˆ u v ( ), ( ) θ ≥ ≤ α β θ θ θ 等价于 θ ≥ θ θ ) ≤ θ ˆ ) , ( ˆ a ( b ˆ ˆ P a( (θ ) ) ≥ = θ α, P ( b (θ ) ) ≤ = θ β. θ ≤ θ ≤ θ )) = 1 − α − β ˆ ) ( ˆ P ( a ( b u ( ), ( ) 在 α β θ υ θ 之间的区域称为置信带。 ˆ a b, θ θ θ 在不知道真值 的情况下,通过估计 值 与函数 给出 的置信区间

经典置信区间(续二) 区间a(0),b(0)]称为具有置信水平或覆盖概率1-o-B的置信区间。 它的深刻含义是包含真实参数的概率为1--B 注意,该区间是随机的,真值0是一个未知常数。 通常情况下,将区间[a,b]报告为0,即c=0-a,d=b-0。 那么0=80.250g 意味着什么呢?它并不意味着任意一次实验: P(80.00<0<80.56)=1-0-B 而是意味着:重复同样样本大小的实验多次,每次按同样的描述构造置信 区间,有1-α-B部分的实验,置信区间将覆盖0。 有时,只有指定的a或B 单边区间(极限) 通常,取a=B=y2 覆盖概率为1-y 中心置信区间 注意:中心置信区间并不意味着区间对于0是对称的,它仅因为=B。 粒子物理与核物理的误差惯例是:68.3%的中心置信区间。 7
7 经典置信区间 (续二 ) 它的深刻含义是 注意,该区间是随机的,真值 θ 是一个未知常数。 ˆ ˆ 区间[ ( a b θ θ ), ( )] 1 称为具有置信水平或覆盖概率 − − α β 的置信区间。 包含真实参数的概率为 1 - α - β ˆ ˆ ˆ [ , ] , , d c a b θ c θ θ a d b + 通常情况下,将区间 报 即 告为 − = − = − 。 0.31 0.25 ˆθ 80.25 + 那么 = − 意味着什么呢?它并不意味着任意一次实验: P (80.00 < θ < 80.56 ) = 1 − α − β 而是意味着:重复同样样本大小的实验多次,每次按同样的描述构造置信 区间,有 1 - α - β 部分的实验,置信区间将覆盖 θ。 通常,取 α= β=γ /2 有时,只有指定的 α 或 β 单边区间 (极限 ) 粒子物理与核物理的误差惯例是:68.3%的中心置信区间。 覆盖概率为1-γ 中心置信区间 ˆ 注 意:中心置信区间并不意味着区间对于θ α 是对称的,它仅因为 = β
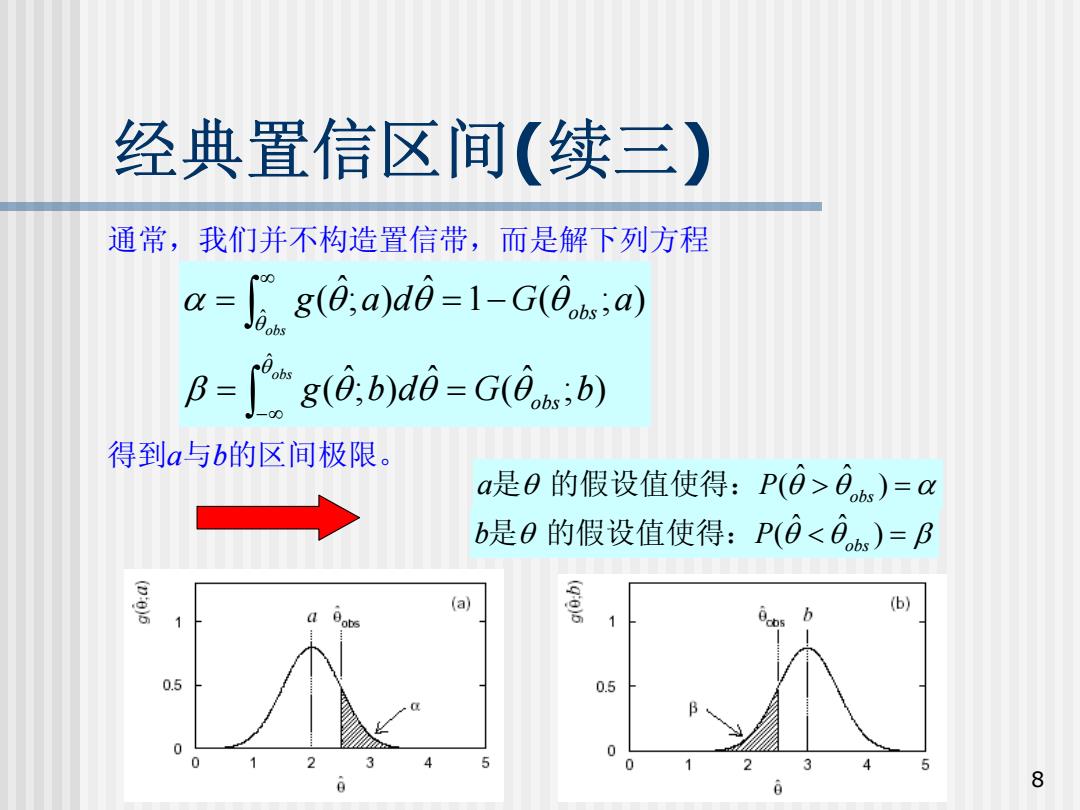
经典置信区间(续三) 通常,我们并不构造置信带,而是解下列方程 ax=gg(d,a)d0=1-G(⑥,;a) B=g(0:b)d0-G(0:b) 得到a与b的区间极限。 a是B的假设值使得:P(0>0,s)=au b是0的假设值使得:P(0<0s)=B (a) (b) bs 0.5 0.5 0 0 3 5 0 8
8 经典置信区间 (续三 ) 通常,我们并不构造置信带,而是解下列方程 得到 a 与 b的区间极限。 ; ) ˆ ( ˆ ; ) ˆ ( ; ) ˆ 1 ( ˆ ; ) ˆ ( ˆ ˆ g b d G b g a d G a obs obs obs obs β θ θ θ α θ θ θ θ θ = = = = − ∫ ∫ − ∞ ∞ ˆ ˆ () obs a P 是 θ 的假设值使得: θ θ > = α ˆ ˆ () obs b P 是 θ 的假设值使得: θ θ < = β

高斯分布估计量的置信区间 如果存在 n 为了找到0置信区间,解下列方程 e1-G0ao,)1- Cois-a 8-oaa,=n2s6 得到a与b的解 9
9 高斯分布估计量的置信区间 如果存在 为了找到 θ 置信区间,解下列方程 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = 2 ˆ 2 2 ˆ 2 ) ˆ ( exp 2 1 ; ) ˆ ( θ θ σ θ θ πσ g θ θ , ˆ ; , ) ˆ ( , ˆ ; , ) 1 ˆ 1 ( ˆ ˆ ˆ ˆ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = = Φ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = − = − Φ θ θ θ θ σ θ β θ σ σ θ α θ σ b G b a G a obs obs obs obs 得到 a 与 b的解

高斯分布估计量的置信区间(续) 前面的函数G是对于0的累积分布,且 w-2元e 是标准高斯的累积函数,可以证明 a=0-0,Φ'(1-), b=0s+oΦ'(1-B) 这里Φ给出标准高斯的分位点(累积分布的倒数,可以调用CERNLIB 的程序GAUSIN计算)。 Φ(1-0),Φ(1-B)→给出a与b离0有多少标准偏差。 10
10 高斯分布估计量的置信区间 ( 续 ) ∫− ∞ − Φ = x x x e dx' 2 1 ( ) ' / 2 2 π 1 ˆ 1 ˆ ˆ (1 ), ˆ (1 ) obs obs a b θ θ θ σ α θ σ β − − = − Φ − = + Φ − 1 CERN L I B GAUS IN − 这里 Φ 给出标准高斯的分位点(累积分布的倒数,可以调用 的程序 计算)。 ( 1 ), ( 1 ) 1 1 Φ − α Φ − β − − 是标准高斯的累积函数,可以证明 G ˆ 前面的函数 是对于 θ 的累积分布,且 ˆ 给出 a 与 b 离 θ 有多少标准偏差