
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第四讲:统计检验
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第四讲:统计检验

本讲要点 口假设,检验统计量,显著水平,功效 ▣两种假设下的统计检验 ▣纽曼-皮尔森引理 口▣如何构造一个检验统计量 口Fisher甄别函数与神经网络 2
2 本讲要点 假设,检验统计量,显著水平,功效 两种假设下的统计检验 纽曼-皮尔森引理 如何构造一个检验统计量 Fisher甄别函数与神经网络

概率与统计 统计的含义可以通过比较概率理论来理解 概率 统计(参量测定与假设检验) 从理论到数据 从数据到理论 通过计算某些可观测 进行所谓的假设检验,比较理论预 量(例如,平均值,分 期的参量值或分布。从观察的实验 布等)来给出预期的实 数据给出所研究参数的观测值和误 验分布。 差,并且在某一置信水平上检验理 例如:若宇称守衡, 论的正确与否。 对一特定衰变分布有 例如:观测到一特定衰变分布,是 什么影响? 否可断定宇称守衡? 3
3 概率与统计 统计的含义可以通过比较概率理论来理解 概率 统计 (参量测定与假设检验 ) 从理论到数据 从数据到理论 通过计算某些可观测 量 (例如,平均值,分 布等 )来给出预期的实 验分布。 例如:若宇称守衡, 对一特定衰变分布有 什么影响? 进行所谓的假设检验,比较理论预 期的参量值或分布。从观察的实验 数据给出所研究参数的观测值和误 差,并且在某一置信水平上检验理 论的正确与否。 例如:观测到一特定衰变分布,是 否可断定宇称守衡?
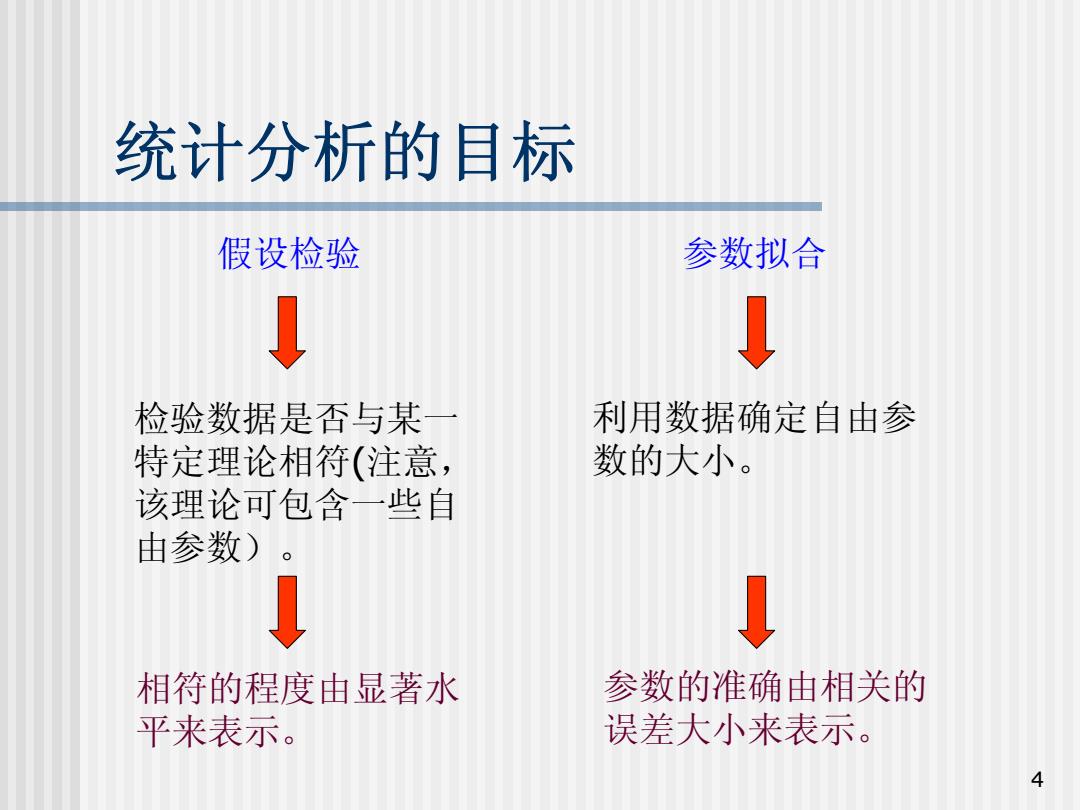
统计分析的目标 假设检验 参数拟合 检验数据是否与某一 利用数据确定自由参 特定理论相符(注意, 数的大小。 该理论可包含一些自 由参数)。 相符的程度由显著水 参数的准确由相关的 平来表示。 误差大小来表示。 4
4 统计分析的目标 假设检验 参数拟合 检验数据是否与某一 特定理论相符 (注意, 该理论可包含一些自 由参数)。 利用数据确定自由参 数的大小。 相符的程度由显著水 平来表示。 参数的准确由相关的 误差大小来表示
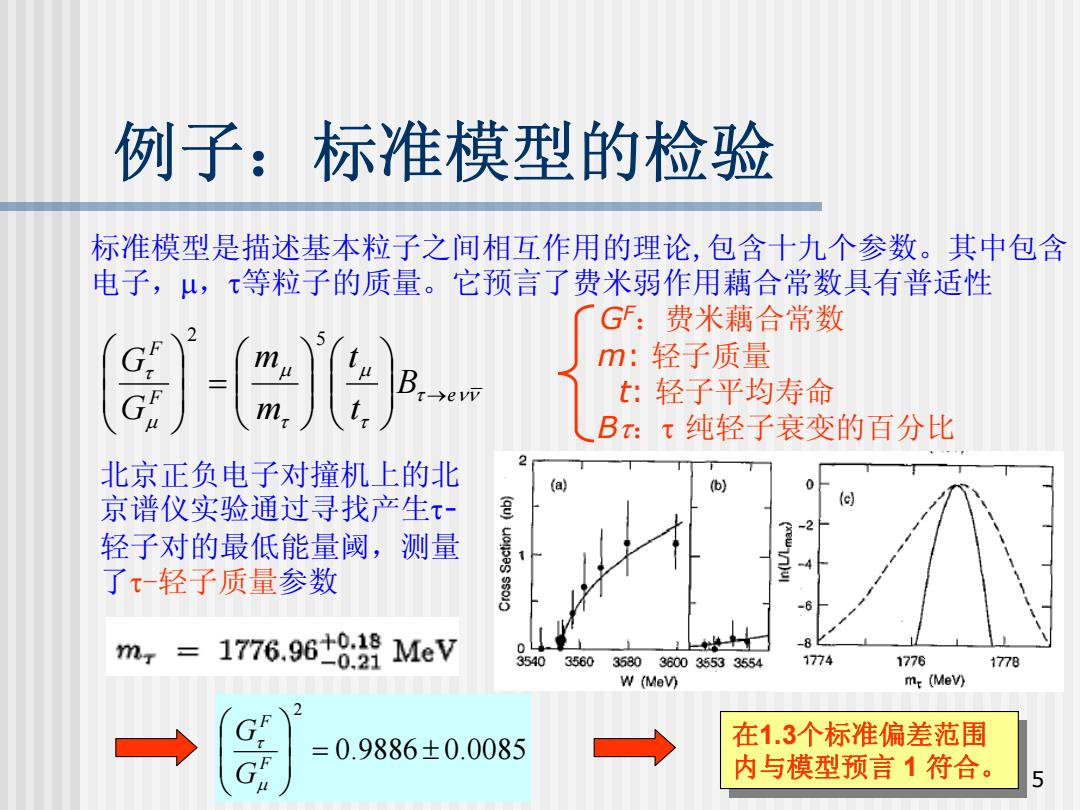
例子:标准模型的检验 标准模型是描述基本粒子之间相互作用的理论,包含十九个参数。其中包含 电子,μ山,等粒子的质量。它预言了费米弱作用藕合常数具有普适性 G:费米藕合常数 m:轻子质量 e vi t:轻子平均寿命 B:τ纯轻子衰变的百分比 北京正负电子对撞机上的北 (a) 京谱仪实验通过寻找产生τ -2 轻子对的最低能量阈,测量 了-轻子质量参数 mr 1776.96±8:8 MeV 3540 3560 3680360035533554 1774 1776 1778 W (Mev) m:(MeV) c- 0.9886±0.0085 在1.3个标准偏差范围 内与模型预言1符合
5 例子:标准模型的检验 标准模型是描述基本粒子之间相互作用的理论,包含十九个参数。其中包含 电子, μ,τ等粒子的质量。它预言了费米弱作用藕合常数具有普适性 τ νν τ μ τ μ μ τ F e F B t t m m G G ⎟ → ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ 2 5 G F:费米藕合常数 m: 轻子质量 t: 轻子平均寿命 B τ:τ 纯轻子衰变的百分比 北京正负电子对撞机上的北 京谱仪实验通过寻找产生 τ - 轻子对的最低能量阈,测量 了 τ-轻子质量参数 0.9886 0.0085 2 = ± ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ F F G G μ τ 在1.3个标准偏差范围 内与模型预言 1 符合。 在1.3个标准偏差范围 内与模型预言 1 符合

假设检验 假如测量结果为元=(x1,x2,,xn), 例如:正负电子对撞后所产生的事例 中,对于每个事例,有下列测量量 x1=产生的带电粒子数;x2=粒子的平均横动子;x?=产生的"喷注"数目; 这里x服从在-维空间的某些与产生事例类型有关的联合概率 密度函数,例如:正负电子对撞,原子核与原子核碰撞,等等。那么 这些联合的概率密度函数f()取决于采取何种假设。 f(|H),f(|H),等等 通常情况下很难处理多维的x问题, 简单假设:f()无未定参数 因此,常常构造低维的统计检验,在 不失去甄别各种假设能力的条件下, 复杂假设:f(;)含未定参数a 使得1()成为精简后的数据样本。 那么此时的统计量t具有概率密度函数g(tH),8(tH)
6 假设检验 " 产生的带电粒子数; 粒子的平均横动子; 产生的"喷注"数目; x1 = x2 = x3 = 0 1 , : , , () ( | ), ( | ), x n f x f x H f x H − G G G G 这里 服从在 维空间的某些与产生事例类型有关的联合概率 密度函数 例如 正负电子对撞 原子核与原子核碰撞 等等。那么 这些联合的概率密度函数 取决于采取何种假设。 等等 1 2 ( , ,..., ), n x x = x x G 假如测量结果为 例如:正负电子对撞后所产生的事例 中,对于每个事例,有下列测量量 : ( ;α) α : ( ) 复杂假设 含未定参数 简单假设 无未定参数 f x f x G G t x 。 , , x , 使得 成为精简后的数据样本 不失去甄别各种假设能 力的条件下 因此 常常构造低维的统计检 验 在 通常情况下很难处理多 维的 问题 ( ) , G G 0 1 那么此时的统计量 t g 具有概率密度函数 (t | H ), g(t | H )

拒绝域、第一与第二类误差 考虑统计检验量t服从g(tHo),g(t|H1),… 8(t) cut 定义拒绝域,使得H。假设为真时,t不大可能 接受Ho拒绝Ho 发生 例如,在上述情况下,t≥tm 如果观测量tos在拒绝域时,拒绝Ho, g(tH) g(t|Ho) 否则接受H。 假若H为真,但被拒绝的可能性构成第一类误差 a=g(tH)dt (显著水平) 假若接受H。,但实际情况却是H为真的可能性构成第二类误差 B=g(tH)dt (1-B=功效) 7
7 拒绝域、第一与第二类误差 0 1 0 ( | ), , ( | .. , t g t H g t H ) . H t 考虑统计检验量 服从 定义拒绝域 使得 假设为真时,不大可能 发生 ( | ) H0 g t ( | ) H1 g t 接受 H 0 拒绝 H 0 ∫ ∞ = cut t g ( t | H )dt α 0 ∫− ∞ = cut t g ( t | H )dt β 1 g ( t ) (1- β =功效 ) (显著水平 ) t cut t cut 例如,在上述情况下 , t ≥ t 0 0 , , obs t H H 如果观测量 在拒绝域时 拒绝 否则接受 。 0 假若 H 为真,但被拒绝的可能性构成 第一类误差 0 1 假若接受H H ,但实际情况却是 为真的可能性构成第二类误差
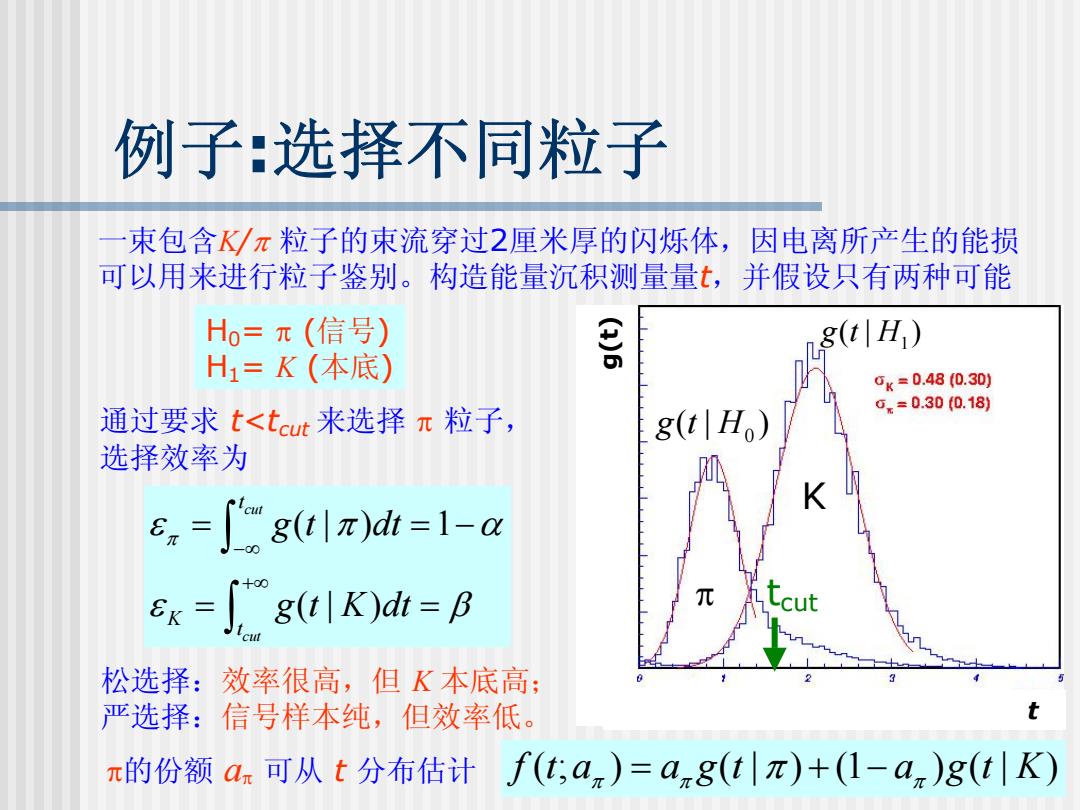
例子:选择不同粒子 束包含K/π粒子的束流穿过2厘米厚的闪烁体,因电离所产生的能损 可以用来进行粒子鉴别。构造能量沉积测量量,并假设只有两种可能 H0=元(信号) g(tH) H1=K(本底) 0k=0.48(0.30) o.=0.30(0.18) 通过要求t<tcut来选择π粒子, g(t|Ho) 选择效率为 c.=∫gtlπ)dh=1-a Ex=g(tK)di=B 松选择:效率很高, 但K本底高: 严选择: 信号样本纯,但效率低。 π的份额a元可从t分布估计 f(t;an)=an8(t|π)+(1-an)g(t|K)
8 例子:选择不同粒子 一束包含K/π 粒子的束流穿过2厘米厚的闪烁体,因电离所产生的能损 可以用来进行粒子鉴别。构造能量沉积测量量t,并假设只有两种可能 K π H0= π (信号) H1= K (本底) t g(t) tcut 1 g t( | H ) 0 通过要求 t<tcut 来选择 π 粒子, g(t H| ) 选择效率为 ( | ) 1 ( | ) cut cut t K t g t dt g t K dt π ε π α ε β −∞ +∞ = = − = = ∫ ∫ 松选择:效率很高,但 K 本底高; 严选择:信号样本纯,但效率低。 π的份额 aπ 可从 t 分布估计 f ( ;t a ) a g(t | ) (1 a )g(t | K) π π = + π − π
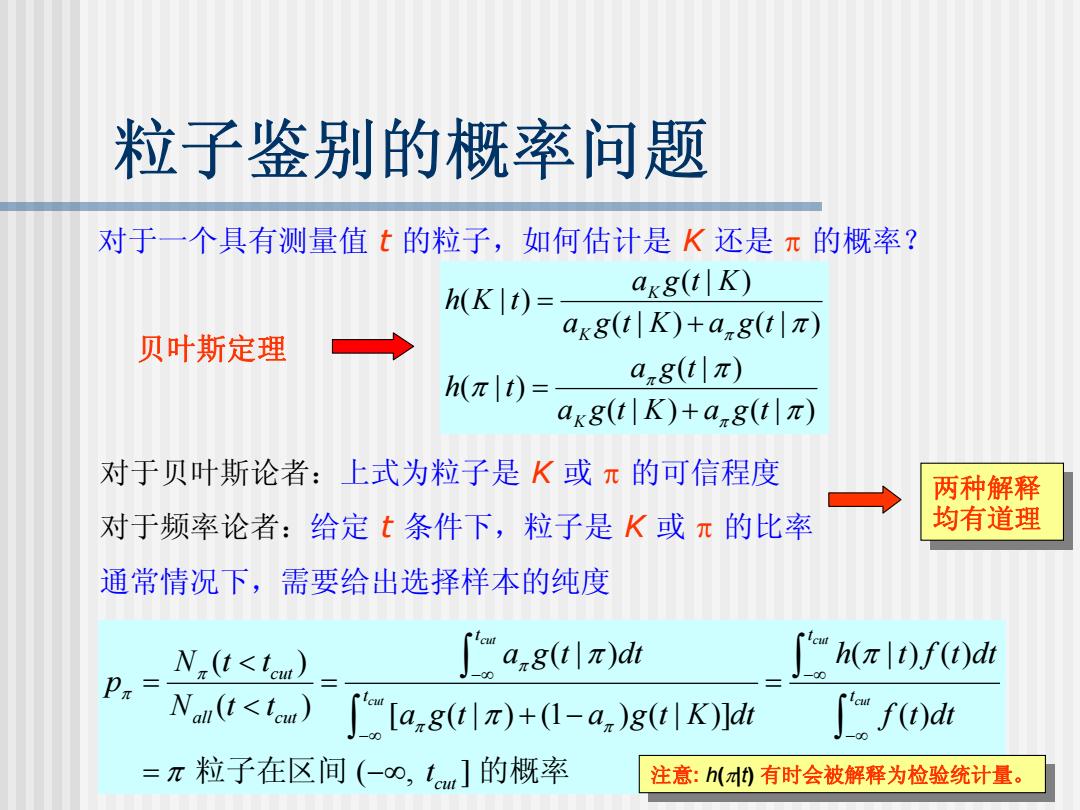
粒子鉴别的概率问题 对于一个具有测量值t的粒子,如何估计是K还是π的概率? h(K t)= akg(t|K akgt|K)+ang(tπ) 贝叶斯定理 h(πlt)= an8(t|π) axg(t|K)+ang(t|π) 对于贝叶斯论者:上式为粒子是K或π的可信程度 两种解释 对于频率论者:给定t条件下,粒子是K或π的比率 均有道理 通常情况下,需要给出选择样本的纯度 N(t<teu) a,gtlπ)dt fh(πlt)ft)d Nmt<t.a)∫[a,8tlπ)+l-a,)gtlK)adh ∫fu)d =π粒子在区间(-o,tm]的概率 注意:h(有时会被解释为检验统计量
9 粒子鉴别的概率问题 对于一个具有测量值 t 的粒子,如何估计是 K 还是 π 的概率? ( | ) ( | ) ( | ) ( | ) ( | ) ( | ) ( | ) ( | ) π π π π π π π a g t K a g t a g t h t a g t K a g t a g t K h K t K K K + = + = 贝叶斯定理 通常情况下,需要给出选择样本的纯度 ( | ) ( | ) ( ) ( ) ( ) [ ( | ) ( 1 ) ( | )] ( ) ( , ] cut cut cut cut t t cut t t all cut cut N t a g t d t h t f t dt t p N t t a g t a g t K dt f t d t t π π π π π π π π π −∞ −∞ −∞ −∞ < = = = < + − = − ∞ ∫ ∫ ∫ ∫ 粒子在区间 的概率 注意注意: : h h (π (π |t | ) t)有时会被解释为检验统计量。 有时会被解释为检验统计量。 对于贝叶斯论者:上式为粒子是 K 或 π 的可信程度 对于频率论者:给定 t 条件下,粒子是 K 或 π 的比率 两种解释 均有道理 两种解释 均有道理

纽曼-皮尔森引理与拒绝域 考虑一个多维检验统计量(t1,,m),有信号假设Ho与本底假设H1 问题:如何选择一个最佳的拒绝域或者 cut? 纽曼-皮尔森引理:在给定效率条件下,要得到最高纯度的信号样本,或 者在给定的显著水平下得到最高的功效,可以选择下列接受域来实现 g(t H) >c=用以决定效率的常数 g(tH) 对于不含未定参量的最优化一维检验统计量, g(t|Ho) 简单假设Ho与H1的似然之比 g(H) 实际应用中,“最好是单值函数。 10
10 纽曼- 皮尔森引理与拒绝域 考虑一个多维检验统计量 t=(t1,…,tm) ,有信号假设H0与本底假设H1。 问题:如何选择一个最佳的拒绝域或者 cut? 纽曼-皮尔森引理:在给定效率条件下,要得到最高纯度的信号样本,或 者在给定的显著水平下得到最高的功效,可以选择下列接受域来实现 用以决定效率的常数 ( | ) ( | )10 > c = g t H g t H GG 对于不含未定参量的最优化一维检验统计量, ( | ) ( | ) 1 0 g t H g t H r G G = 简单假设H0与H1的似然之比 实际应用中,r 最好是单值函数