
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第一讲:基本概念 http://hep.tsinghua.edu.cn/~chensm/lectures/lecture_1.ppt
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第一讲:基本概念 http://hep.tsinghua.edu.cn/~chensm/lectures/lecture_1.ppt

本次讲座的要点 ·概率 ■随机变量与函数 ■期待值 ·误差传递
本次讲座的要点 概率 随机变量与函数 期待值 误差传递
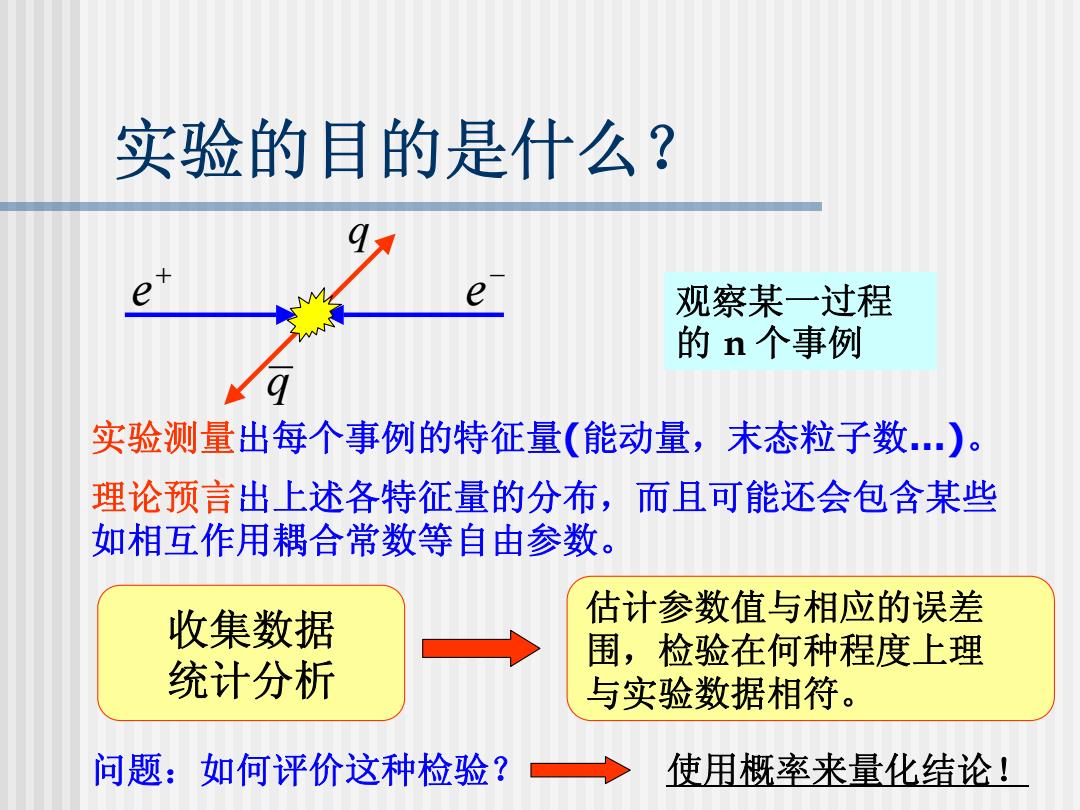
实验的目的是什么? 观察某一过程 的n个事例 实验测量出每个事例的特征量(能动量,末态粒子数.)。 理论预言出上述各特征量的分布,而且可能还会包含某些 如相互作用耦合常数等自由参数。 收集数据 估计参数值与相应的误差 围,检验在何种程度上理 统计分析 与实验数据相符。 问题:如何评价这种检验? 使用概率来量化结论!
实验的目的是什么? + e − e q q 观察某一过程 的 n 个事例 实验测量出每个事例的特征量 (能动量,末态粒子数…) 。 理论预言出上述各特征量的分布,而且可能还会包含某些 如相互作用耦合常数等自由参数。 收集数据 统计分析 估计参数值与相应的误差 围,检验在何种程度上理 与实验数据相符。 问题:如何评价这种检验? 使用概率来量化结论!

随机事例 在一定的实验条件下,现象A可能发生,也 可能不发生,并且只有发生或不发生这样两 种可能性,这是偶然现象中一种比较简单的 形态,我们把发生了现象A的事例称为随机 事例A,简称事例A
随机事例 在一定的实验条件下,现象A可能发生,也 可能不发生,并且只有发生或不发生这样两 种可能性,这是偶然现象中一种比较简单的 形态,我们把发生了现象A的事例称为随机 事例A,简称事例A
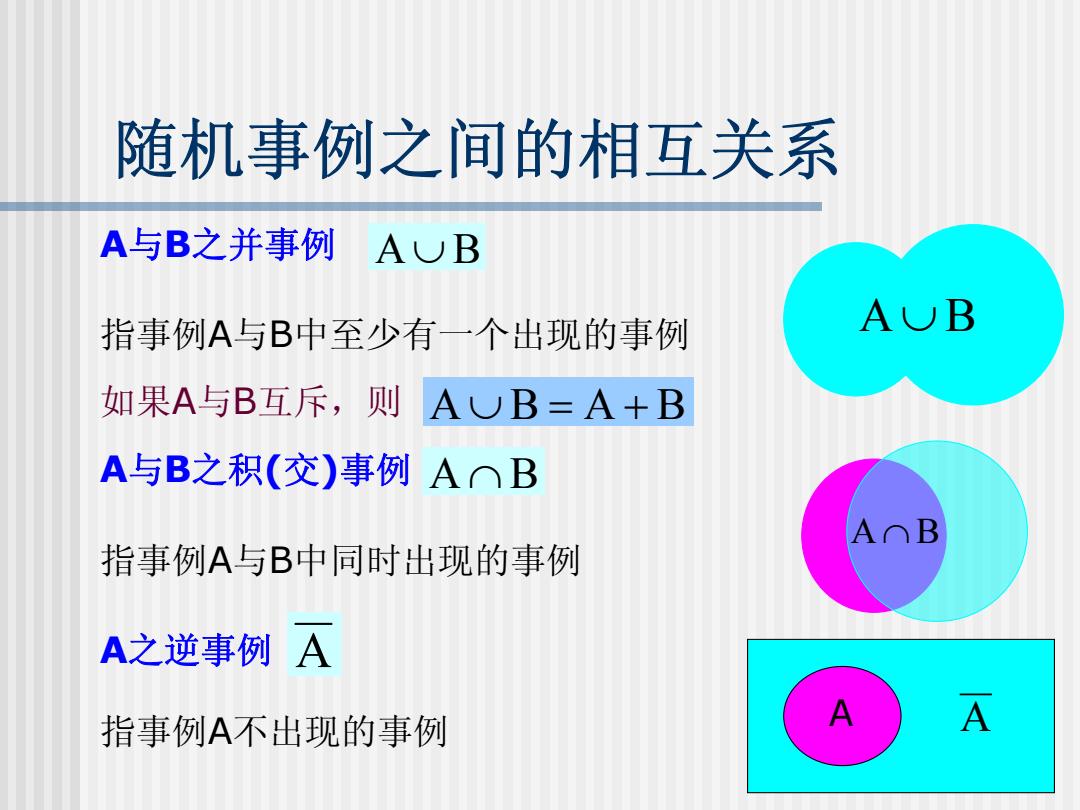
随机事例之间的相互关系 A与B之并事例 AB 指事例A与B中至少有一个出现的事例 AB 如果A与B互斥,则AUB=A+B A与B之积(交)事例AOB 指事例A与B中同时出现的事例 A之逆事例A 指事例A不出现的事例 A
随机事例之间的相互关系 A 与 B之并事例 A 与 B之积 ( 交 )事例 A ∪ B A之逆事例 A ∩ B 指事例 A 与 B中至少有一个出现的事例 指事例 A 与 B中同时出现的事例 A 指事例 A不出现的事例 A A A ∪ B A ∩ B 如果 A 与 B互斥,则 A ∪ B = A + B

概率的定义 柯尔莫哥洛夫公理:考虑一全集S具有子集A,B,.. AcS,P(A)≥0 P(S)=1 P(A)称为事 例A的概率 A∩B=O→P(AUB)=P(A)+P(B) 从该公理可以导出下列概率公式 P(A)=1-P(A) S P(AUA)=1 A ACB→P(A)≤P(B) P(AUB)=P(A)+P(B)-P(AOB)
概率的定义 柯尓莫哥洛夫公理:考虑一全集 S具有子集 A , B , … A B 0 P(A B) P(A) P(B) P(S) 1 A S,P(A) 0 ∩ = ⇒ ∪ = + = ⊂ ≥ P(A B) P(A) P(B) P(A B) A B P(A) P(B) P(A A ) 1 P( A ) 1 P(A) ∪ = + − ∩ ⊂ ⇒ ≤ ∪ = = − 从该公理可以导出下列概率公式 A B C S P(A)称为事 例 A的概率

条件概率 假设B出现的概率不为零,在给定B的情况下出现A的条件概 率定义为 P(A∩B) P(AB)= P(B) 如果P(A⌒B)=P(A)P(B) 则表明A与B相互独立。 如果A与B相互独立,则有 P(AB)= P(A)P(B) =P(A) 结果与B无关 P(B) 注意:与不相交的子集定义不同A⌒B
条件概率 假设B出现的概率不为零,在给定B的情况下出现A的条件概 率定义为 P(B) P(A B) P(A | B) ∩ = 如果 P(A ∩ B) = P(A)P(B) 则表明A与B相互独立。 如果A与B相互独立,则有 P(A) P(B) P(A)P(B) P(A | B) = = 注意: 与不相交的子集定义不同 A ∩ B 结果与B无关

概率的含义 >相对频率 假设A,B,…是一可重复实验的结果,则概率就是 结果为A P(A)=lim n→0 n次实验 >主观概率 如果A,B,,是假设(是真或是假的各种陈述),那么概率 P(A)=对A为真的信心程度 两种解释皆与柯尔莫哥洛夫公理相符。 概率的频率解释在数据分析中用起来比较自然,但是…
概率的含义 ¾相对频率 假设 A , B , …是一可重复实验的结果,则概率就是 n n次实验 结果为 A P(A) lim → ∞ = ¾主观概率 如果 A , B , … 是假设 (是真或是假的各种陈述 ),那么概率 P(A) = 对A为真的信心程度 9两种解释皆与柯尔莫哥洛夫公理相符。 9概率的频率解释在数据分析中用起来比较自然,但是 … 9两种解释皆与柯尔莫哥洛夫公理相符。 9概率的频率解释在数据分析中用起来比较自然,但是 …
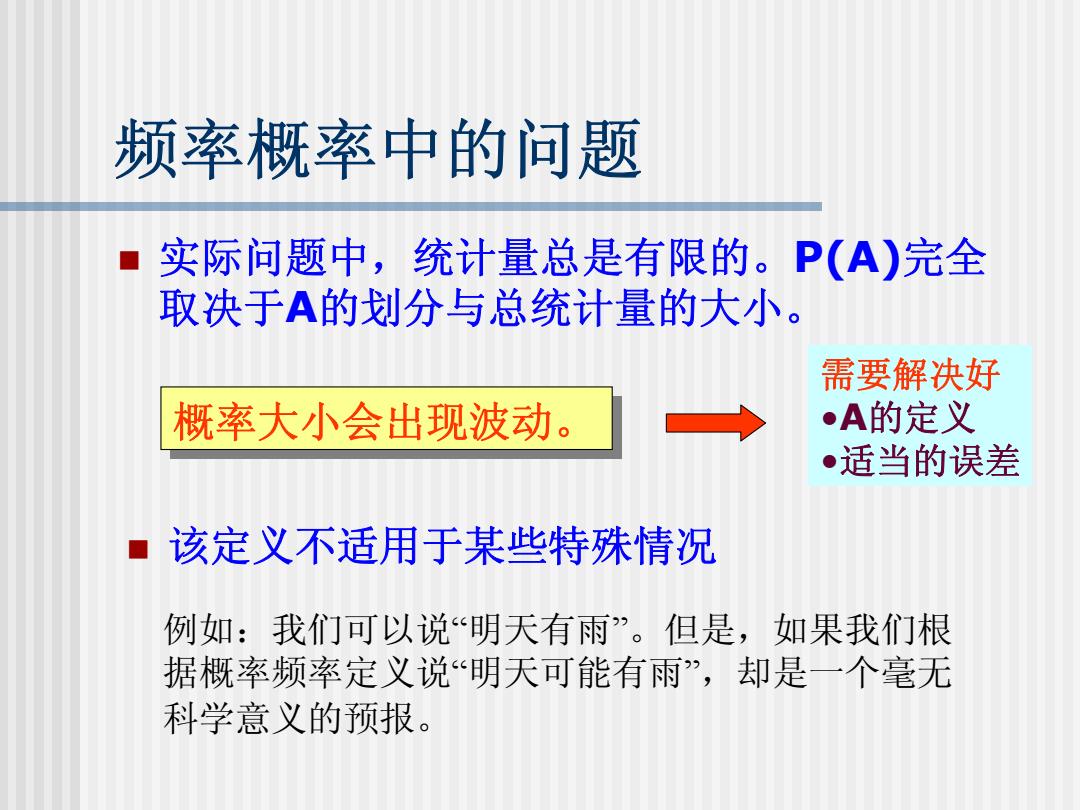
频率概率中的问题 实际问题中,统计量总是有限的。P(A)完全 取决于A的划分与总统计量的大小。 需要解决好 概率大小会出现波动。 ●A的定义 ●适当的误差 该定义不适用于某些特殊情况 例如:我们可以说“明天有雨”。但是,如果我们根 据概率频率定义说明天可能有雨”,却是一个毫无 科学意义的预报
频率概率中的问题 实际问题中,统计量总是有限的。P(A)完全 取决于 A的划分与总统计量的大小。 概率大小会出现波动。 概率大小会出现波动。 例如:我们可以说 “明天有雨 ”。但是,如果我们根 据概率频率定义说 “明天可能有雨 ”,却是一个毫无 科学意义的预报。 该定义不适用于某些特殊情况 需要解决好 • A的定义 •适当的误差
主观概率中的问题 主观性:在对同一随机现象的描述中,我的 P(理论)与你的P(理论)可能不同 理论家甲 理论家乙 之理论A 之理论B 使用主观概率的原因 •出于绝望 ·出于无知 X ·出于懒惰
主观概率中的问题 主观性:在对同一随机现象的描述中,我的 P(理论 )与你的P(理论 )可能不同 理论家甲 之理论 A 理论家乙 之理论 B •出于绝望 9 •出于无知 ² •出于懒惰 V 使用主观概率的原因