
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第八讲:最大似然法(II) 1
1 粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第八讲:最大似然法(II)

本讲要点 双参数情况下的最大似然法举例 利用MINUIT数值求解最小值 推广的最大似然法 ■ 利用最大似然法处理分区数据 检验最大似然法的拟合优度 与贝叶斯参数估计之间的关系 2
2 本讲要点 双参数情况下的最大似然法举例 利用MINUIT数值求解最小值 推广的最大似然法 利用最大似然法处理分区数据 检验最大似然法的拟合优度 与贝叶斯参数估计之间的关系

例子:最大似然法处理双参数 考虑散射角分布x=C0SO f(x;a,B)= 1+ax+Bx 2+2B/3 在实际情况下, 探测器也许不可能做全空间探测,即xmn<x<Xmax 这个时候需要考虑效率影响,并对函数进行归一化处理,例如 E效率()= Xmin <X<Xmax 否则 →,f(xa,B)·e(x)dk=1 例如:对于参数为a=0.5,B-0.5,探测器有效范围xmim=-0.95,xmax0.95, 产生n=2000个蒙特卡罗事例,研究用最大似然法处理双参数的问题
3 例子:最大似然法处理双参数 考虑散射角分布 例如:对于参数为α=0.5,β=0.5,探测器有效范围 x min=-0.95, x max= 0.95, 产生 n=2000个蒙特卡罗事例,研究用最大似然法处理双参数的问题。 x = cosθ 2 2 / 3 1 ( ; , ) 2 β α β α β ++ + = x x f x min max 在实际情况下,探测器也许不可能做全空间探测,即 x x < < x 。 这个时候需要考虑效率影响,并对函数进行归一化处理,例如 1 1 f ( ; x x α β, ) ε ( )dx 1 − ⋅ = ∫ θ min max 1 ( ) 0 x x x ε x ⎧ < < = ⎨⎩ 效率 否则
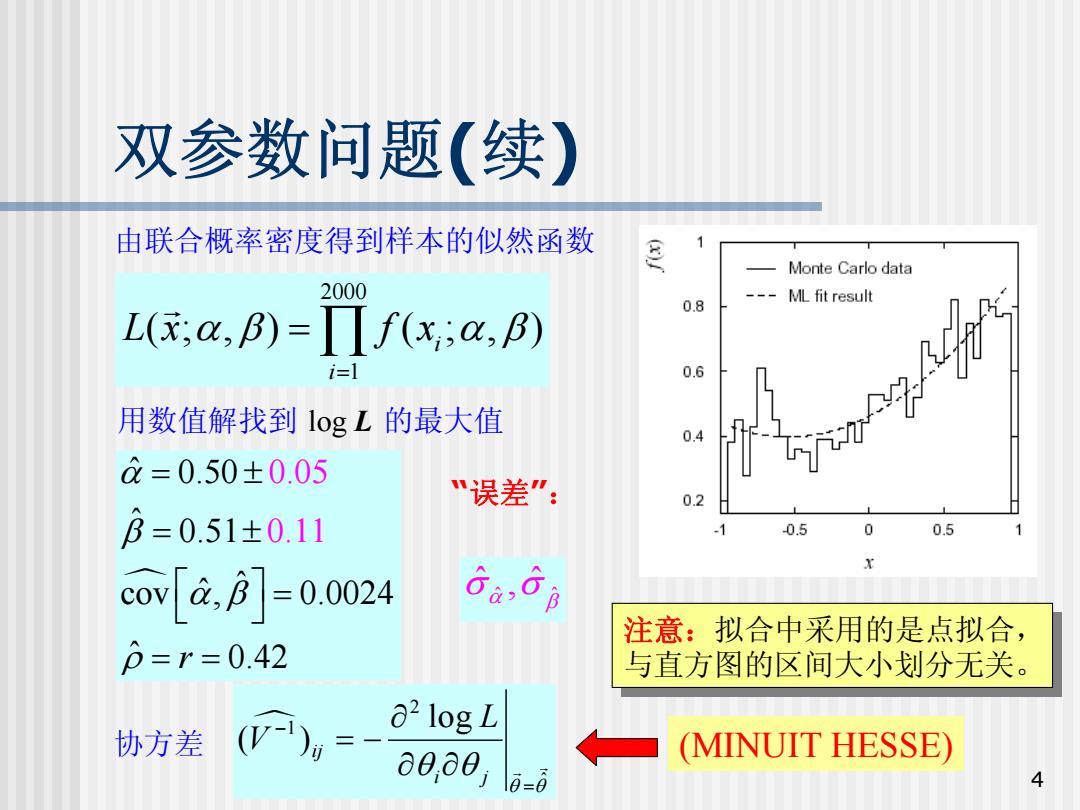
双参数问题(续) 由联合概率密度得到样本的似然函数 Monte Carlo data 2000 0.8 ML fit result L(x;a,B)=f(x;;a,B) i=l 0.6 用数值解找到logL的最大值 04 a=0.50±0.05 "误差” 0.5 B=0.51±0.11 0.5 0.5 X cov[a,B]=0.0024 6 6 注意:拟合中采用的是点拟合, p=r=0.42 与直方图的区间大小划分无关。 () a2 log L 协方差 a0,a0 (MINUIT HESSE) 6=0 4
4 双参数问题 ( 续 ) 用数值解找到 log L 的最大值 m ˆ 0.50 ˆ 0.51 ˆ c o v ˆ, 0.0024 ˆ 0.4 0.05 0.1 2 1 r α β α β ρ = ± = ± ⎡ ⎤ = ⎣ ⎦ = = 协方差 m 2 1 ˆ lo g ( )ij i j L V θ θ θ θ − = ∂ = − ∂ ∂ G G “误差 ”: ˆ ˆ ˆ ˆ , α β σ σ 由联合概率密度得到样本的似然函数 2000 1 ( ; , ) ( ; , ) i i L x α β α f x β = = ∏ G (MINUIT HESSE) 注意:拟合中采用的是点拟合, 与直方图的区间大小划分无关。 注意:拟合中采用的是点拟合, 与直方图的区间大小划分无关
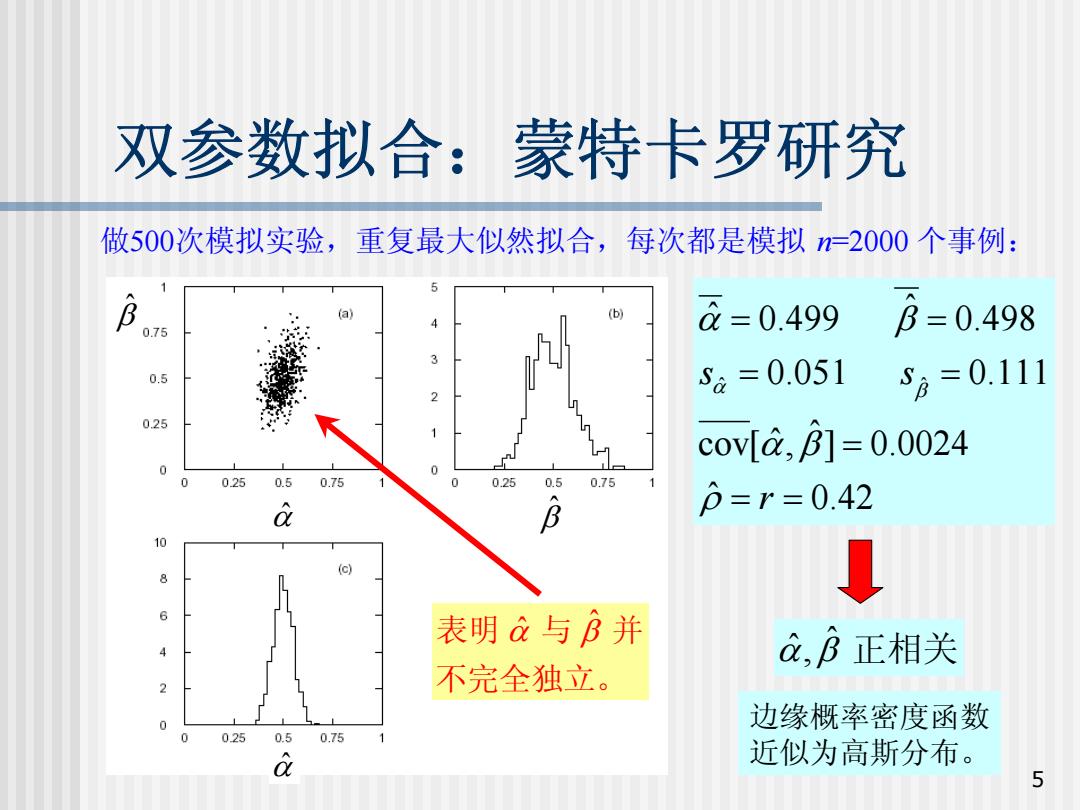
双参数拟合:蒙特卡罗研究 做500次模拟实验,重复最大似然拟合,每次都是模拟=2000个事例: B (a) (b) a=0.499 p=0.498 .75 0.5 s6=0.051 SB=0.111 0.25 cov[a,B]=0.0024 0 025 0.5 0.75 0.25 0.5 0.75 B p=r=0.42 0 (c) 表明a与B并 C,B正相关 不完全独立。 0 边缘概率密度函数 025 0.5 0.75 a 近似为高斯分布。 5
5 双参数拟合:蒙特卡罗研究 做500次模拟实验,重复最大似然拟合,每次都是模拟 n=2000 个事例: ˆ ˆ ˆ ˆ 0.499 0.498 0.051 0.111 ˆ c o v [ ˆ, ] 0.0024 ˆ 0.42 s s r α β α β α β ρ = = = = = = = ˆ α β ˆ, 正相关 边缘概率密度函数 αˆ 近似为高斯分布。 β ˆ αˆ β ˆ ˆ 表明 α β ˆ 与 并 不完全独立

双参数拟合:logL等高线 在前面蒙特卡罗样本中,其中的 0.7 次拟合结果在,B平面表示为 0.6 0.5 true value ML fit result 0.4 对于大的样本容量n,logL具有下列 0.3 形式: 0.3 0.4 0.5 0.6 0.7 C log L(a,B)=log Lmax =川84 6
6 双参数拟合 :log L 等高线 在前面蒙特卡罗样本中,其中的 一次拟合结果在 α, β 平面表示为 对于大的样本容量 n,log L 具有下列 形式: ma x 2 2 2 ˆ ˆ ˆ ˆ lo g ( , ) lo g ˆ ˆ 1 ˆ ˆ 2 2( 1 ) L L α α β β α β α α β β α α β β ρ ρ σ σ σ σ = ⎡ ⎤ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ − − ⎛ ⎞ − − ⎢ ⎥ − + ⎜ ⎟ − ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ − ⎢ ⎜ ⎟ ⎜ ⎟⎥ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦

双参数拟合logL等高线(续) 等高线logL(a,β)-log L max-么是根据下式定义得到的 j 其中,等高线的切线给出了标准偏差 注意:参数之间相关的效应体 椭圆的倾角与相关系数有关 现在对估计量的误差或方差方 面的影响(或偏大或偏小)。 2poa tan2φ= 7
7 双参数拟合 :log L 等高线 ( 续 ) 等高线 log L ( α,β)=log L ma x – ½ 是根据下式定义得到的 2 2 2 ˆ ˆ ˆ ˆ ˆ ˆ 1 ˆ ˆ 2 1 1 α α β β α α β β α α β β ρ ρ σ σ σ σ ⎡ ⎤ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ − − ⎛ ⎞ − − ⎢ ⎥ + ⎜ ⎟ − = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ − ⎢ ⎥ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ 其中,等高线的切线给出了标准偏差 椭圆的倾角与相关系数有关 α β σ ˆ σ ˆ , 2 ˆ 2 ˆ 2 ˆ ˆ tan 2 α β α β σ σ ρσ σ φ − = 注意:参数之间相关的效应体 现在对估计量的误差或方差方 面的影响 (或偏大或偏小 )。 注意:参数之间相关的效应体 现在对估计量的误差或方差方 面的影响 (或偏大或偏小 )

一个实用的求函数最小值程序 在核与粒子物理研究中,大家普遍使用的求函数最小值程序是 MINUIT软件包 http://hep.tsinghua.edu.cn/~chensm/lectures/minuit.pdf 求logL最大值等效于求-logL的最小值。 它可以对目标函数为似然函数,最小二乘函数或用户自定义函数求极值。 它提供了几种最小化过程和相应的误差分析。原初版本用Fortran语言。 写于25年前,用于当时西欧核子中心(CERN)的实验数据分析。现也被 应用于粒子物理以外的领域。目前,在核与粒子物理研究中,有三种使 用方式 >在MINUIT框架下单独使用(适于data-driven模式): >在物理分析工作站(PAW)环境下互动调用MINUIT软件包(基于Fortran); >在PAW升级软件包ROOT环境下互动调用MINUIT软件包(基于C++)。 8
8 一个实用的求函数最小值程序 在核与粒子物理研究中,大家普遍使用的求函数最小值程序是 MINUIT 软件包 它可以对目标函数为似然函数,最小二乘函数或用户自定义函数求极值。 它提供了几种最小化过程和相应的误差分析。原初版本用Fortran语言。 写于25年前,用于当时西欧核子中心 (CERN )的实验数据分析。现也被 应用于粒子物理以外的领域。目前,在核与粒子物理研究中,有三种使 用方式 ¾ 在MINUIT框架下单独使用 (适于data-driven模式 ); ¾在物理分析工作站(PAW)环境下互动调用MINUIT软件包 (基于Fortran); ¾ 在PAW升级软件包ROOT环境下互动调用MINUIT软件包 (基于C++ )。 求 log L 最大值等效于求 –log L 的最小值。 http://hep.tsinghua.edu.cn/~chensm/lectures/minuit.pdf

MINUIT数值求解极小值(1) 实际应用中,通常采用-ogL()的形式来求最小值。例如,对前面的例子 program MINUIT FIT c Minimize using SIMPLEX and MIGRAD,get covariance implicit NONE c matrix with HESSE integer npar call MNEXCM(FCN,'SIMPLEX',arglis,0,ierr,0) parameter(npar=2) call MNEXCM(FCN,'MIGRAD,arglis,0,ierr,0) character*10 chnam(npar) call MNEXCM(FCN,'HESSE,arglis,0,ierr,0) integer ierr,ird,isav,istat,ivarbl,iwr c Get result of fit(for least squares,fmin is chi2) integer npari,nparx call MNSTAT(fmin,fedm,errdef,npari,nparx,istat) double precision arglis(10),bndl,bnd2,deriv(npar),dpar(npar) call MNPOUT(1,chnam(1),par(1),dpar(1),bnd1,bnd2,ivarbl) double precision fmin,fedm,errdef,covmat(npar,npar),log I call MNPOUT(2,chnam(2),par(2),dpar(2),bnd1,bnd2,ivarbl) external FCN call MNEMAT(covmat,npar) double precision par(npar) log 1=-0.5*fmin c Initialize MINUIT,set print level to-1 write(6,*)'Fit results:' ird=5!unit number for input to Minuit(keyboard) write(6,*) iwr=6!unit number for output from Minuit(screen) write(6,*)'alpha =,par(1),'+/-',dpar(1) isav=7 unit number for use of the SAVE command write(6,*)'beta =,par(2),'+-',dpar(2) call MNINIT(ird,iwr,isav) write(6,*)'cov[alpha,beta]=',covmat(1,2) arglis(1)=-1.d0 write(6,*)'rho[alpha,beta]=',covmat(1,2)/(dpar(1)*dpar(2)) call MNEXCM(FCN,'SET PRIN,arglis,1,ierr,0) write(6,*)'log 1 =,log 1 c Define parameters alpha and beta,give initial values and step sizes stop call MNPARM(1,alpha,0.5d0,0.1d0,0.d0,0.d0,ierr) end call MNPARM(2,beta,0.5d0,0.1d0,0.d0,0.d0,ierr) c Get input data by calling FCN with iflag=l arglis(1)=1.do 编译:f77 minuit fit,f-o minuit fit`cernlib call MNEXCM(FCN,'CALL,arglis,1,ierr,0) 运行:minuit fit
9 MINUIT数值求解极小值(1) − log L(θ ) G 实际应用中,通常采用 的形式来求最小值。例如,对前面的例子 program MINUIT_FIT implicit NONE integer npar parameter (npar=2) character*10 chnam(npar) integer ierr, ird, isav, istat, ivarbl, iwr integer npari, nparx double precision arglis(10), bnd1, bnd2, deriv(npar), dpar(npar) double precision fmin, fedm, errdef, covmat(npar,npar), log_l external FCN double precision par(npar) c Initialize MINUIT, set print level to -1 ird = 5 ! unit number for input to Minuit (keyboard) iwr = 6 ! unit number for output from Minuit (screen) isav= 7 ! unit number for use of the SAVE command call MNINIT(ird,iwr,isav) arglis(1)=-1.d0 call MNEXCM(FCN,'SET PRIN',arglis,1,ierr,0) c Define parameters alpha and beta, give initial values and step sizes call MNPARM(1,'alpha',0.5d0,0.1d0,0.d0,0.d0,ierr) call MNPARM(2,'beta ',0.5d0,0.1d0,0.d0,0.d0,ierr) c Get input data by calling FCN with iflag=1 arglis(1)=1.d0 call MNEXCM(FCN,'CALL',arglis,1,ierr,0) c Minimize using SIMPLEX and MIGRAD, get covariance c matrix with HESSE call MNEXCM(FCN,'SIMPLEX',arglis,0,ierr,0) call MNEXCM(FCN,'MIGRAD',arglis,0,ierr,0) call MNEXCM(FCN,'HESSE',arglis,0,ierr,0) c Get result of fit (for least squares, fmin is chi2) call MNSTAT(fmin,fedm,errdef,npari,nparx,istat) call MNPOUT(1,chnam(1),par(1),dpar(1),bnd1,bnd2,ivarbl) call MNPOUT(2,chnam(2),par(2),dpar(2),bnd1,bnd2,ivarbl) call MNEMAT(covmat,npar) log_l=-0.5*fmin write(6,*)'Fit results:' write(6,*) write(6,*)'alpha =',par(1),'+/-',dpar(1) write(6,*)'beta =',par(2),'+/-',dpar(2) write(6,*)'cov[alpha,beta]=',covmat(1,2) write(6,*)'rho[alpha,beta]=',covmat(1,2)/(dpar(1)*dpar(2)) write(6,*)'log_l =',log_l stop end 编译:f77 minuit_fit.f -o minuit_fit `cernlib` 运行:minuit_fit

MINUIT数值求解极小值(2) 用户应提供似然函数FCN 注意:概率密度函数需要在有 subroutine FCN(npar,grad,chi2,par,iflag,futil) 效测量范围进行归一化处理。 c Input:integer npar number of parameters to fit 如果计算有困难,可以将归一 c double precision par(npar)parameter vector C integer iflag select what to do 化因子作为参数来拟合。这种 c double precision futil optional external function 折衷方法虽简便,但会给其它 c Output:double precision grad(npar)gradient vector(not filled) double precision chi2 function to be minimized 待定参数的确定带来误差。 implicit NONE c Calculate log-likelihood integer npar,iflag alpha=par(1) double precision futil,chi2,par(*),grad(*) beta =par(2) integer n max parameter(n_max=10000) 1og1=0. c Normalization factor for [-angle_cut,angle_cut] integer i,n f nor =2*angle cut+2*beta/3.*angle cut**3 double precision alpha,beta,f,log 1,x(n_max),angle_cut,f_nor do i=1,n c Begin n=2000 f-(1.+alpha*x(i)+beta*x(i)**2)/f_nor angle_cut=0.95 log_1=log_1+DLOG(f) end do if(iflag.eq.1)then get n,array x call GET INPUT_DATA(x,n,n_max,angle_cut) chi2=-2.*log_1 2 gets errors right return end if end 10
10 MINUIT数值求解极小值(2) subroutine FCN(npar,grad,chi2,par,i flag,futil) c Input: integ er npar number of parameters to fit c double precision par(npar) parameter vector c integer iflag s elect what to do c double precision futil optional external function c Output: double precision grad(npar) gradient vector (not filled) c double precision chi2 function to be minimized implicit NONE integ er npar,iflag double precision futil,chi2,par(*),grad(*) integ e r n_max parameter (n_max=10000) integ e r i,n double precision alpha,beta,f,log_l,x(n_max),angle_cut,f_nor c Begin n=2000 angle_cut=0.95 if(iflag.eq.1)then ! get n, array x call GET_INPUT_DATA(x,n,n_max,angle_cut) end if c Calculate log-likelihood alpha = par(1) beta = par(2) log_l = 0. c Normalization factor for [-angle_cut,angle_cut] f_nor = 2*angle_cut+2*beta/3.*angle_cut**3 do i=1,n f=(1. +alpha*x(i)+beta*x(i)**2)/ f_nor log_l=log_l+DLOG(f) end do chi2=-2.*log_l ! 2 gets errors right return end 用户应提供似然函数 FCN 注意:概率密度函数需要在有 效测量范围进行归一化处理。 如果计算有困难,可以将归一 化因子作为参数来拟合。这种 折衷方法虽简便,但会给其它 待定参数的确定带来误差