
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第五讲:统计检验(续) 参数估计中的基本概念
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第五讲:统计检验 ( 续 ) 参数估计中的基本概念

本讲要点 ■检验拟合优度,P值定义与应用 ■信号观测的显著程度 ■皮尔逊的2检验 ·样本、估计量与偏置 ■估计量的平均值、方差与协方差 2
2 本讲要点 检验拟合优度,P-值定义与应用 信号观测的显著程度 皮尔逊的χ2检验 样本、估计量与偏置 估计量的平均值、方差与协方差

一个古老的随机性问题 任意投掷一枚硬币,得到结果为正面与反面的概率都是0.5。 如果有人声称他(她)对此进行了检验。投了20次,得到了17 次正面的结果。那么他(她)能否断定得到正面的概率应该是 p%=0.85±0.08 也就是说与预期值0.5有4个标准偏差呢? 问题:理论上允许这样的极端情况出现吗? 或者说与这样一种极端情况相等或更高的概 率有多大? 3
3 一个古老的随机性问题 任意投掷一枚硬币,得到结果为正面与反面的概率都是0.5 。 如果有人声称他 ( 她 )对此进行了检验。投了20次,得到了17 次正面的结果。那么他 ( 她 )能否断定得到正面的概率应该是 0.85 0.08 h p = ± 也就是说与预期值0.5 有 4个标准偏差呢? 问题:理论上允许这样的极端情况出现吗? 或者说与这样一种极端情况相等或更高的概 率有多大? 问题:理论上允许这样的极端情况出现吗? 或者说与这样一种极端情况相等或更高的概 率有多大?
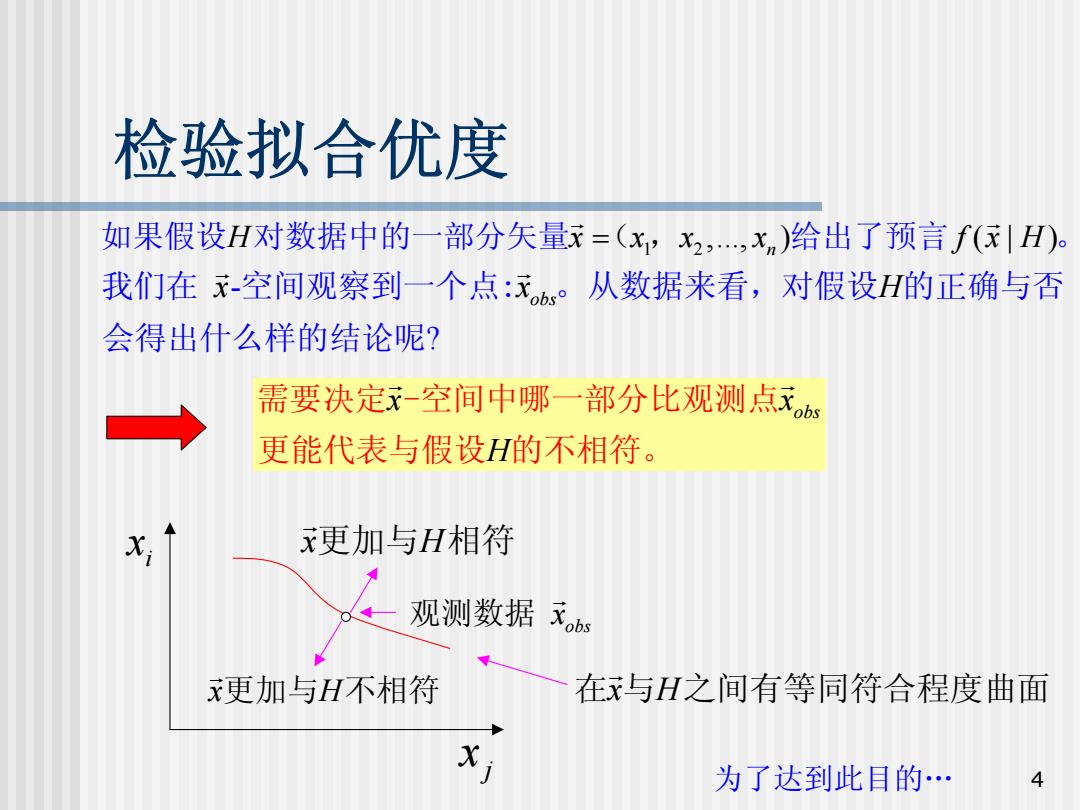
检验拟合优度 如果假设H对数据中的一部分矢量x=(x,x2,,xn)给出了预言f(|H) 我们在元-空间观察到一个点:元°从数据来看,对假设H的正确与否 会得出什么样的结论呢? 需要决定-空间中哪一部分比观测点x6s 更能代表与假设H的不相符。 更加与H相符 观测数据 天obs 更加与H不相符 在x与H之间有等同符合程度曲面 X; 为了达到此目的… 4
4 检验拟合优度 i x j x x H G更加与 不相符 obs x G 观测数据 x H G 在 与 之间有等同符合程度曲面 1 2 ,..., ) ( | ) H n x x = x x f x H G G 如果假设 对数据中的一部分矢量 ( , 给出了预言 。 - ? obs x x H G G 我们在 空间观察到一个点: 。从数据来看,对假设 的正确与否 会得出什么样的结论呢 obs x x H G G 需要决定 -空间中哪一部分比观测点 更能代表与假设 的不相符。 x H G更加与 相符 为了达到此目的…
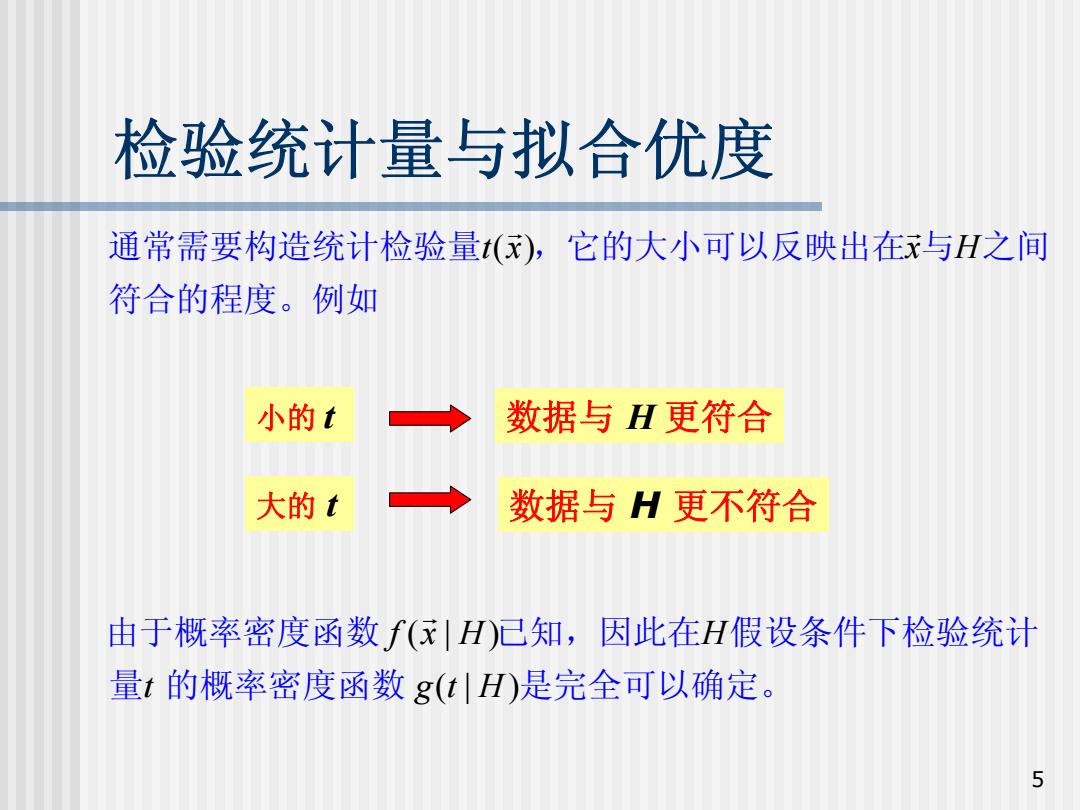
检验统计量与拟合优度 通常需要构造统计检验量(),它的大小可以反映出在x与H之间 符合的程度。例如 小的t 数据与H更符合 大的t 数据与H更不符合 由于概率密度函数f(:|H)已知,因此在H假设条件下检验统计 量t的概率密度函数g(tH)是完全可以确定。 5
5 检验统计量与拟合优度 小的 t (| ) (| ) f x H H t g t H G 由于概率密度函数 已知,因此在 假设条件下检验统计 量 的概率密度函数 是完全可以确定。 数据与 H 更不符合 t x( ) x H G G 通常需要构造统计检验量 ,它的大小可以反映出在 与 之 间 符合的程度。例如 大的 t 数据与 H 更符合

P值定义 将拟合优度用P-值表示(也称为观察的显著水平或置信水平) P=观察到实验数据元或t()像x或t(s)一样, 与假设H具有相同或较小符合程度的概率。 注意:这不是H为真的概率。 在经典统计学上,我们从不涉及P(刊。 而在贝叶斯统计理论中,则把H当成了随机变量,并利用贝叶斯定理 得到 π(H):H的先验概率 P(tH)π(H) P(H)= 「P(tH)π(H)dH 对所有可能性进行归一化积分 6
6 P-值定义 将拟合优度用P-值表示 (也称为观察的显著水平或置信水平) 注意注意: : 这不是 这不是H H 为真的概率。 为真的概率。 在经典统计学上,我们从不涉及 P(H) 。 ∫ = P t H H dH P t H H P H t ( | ) ( ) ( | ) ( ) ( | ) π π π(H):H 的先验概率 对所有可能性进行归一化积分 = ( ) ( ) obs obs P x t x x t x H G G G G 观察到实验数据 或 像 或 一样, 与假设 具有相同或较小符合程度的概率。 而在贝叶斯统计理论中,则把 H 当成了随机变量,并利用贝叶斯定理 得到

P值与假设检验 根据P值的定义,对H假设拟合优度的检验可以通过计算P值的大小 来完成。 但是,应注意以下两点: >在P值定义中不涉及别的假设。 >P值是一个随机变量。前面采用的显著水平在检验时已经被指定为常数。 如果H为真,则对于连续的X,P在[0,1]范围内均匀分布. 如果H非真,则P的概率密度函数通常很接近零。 7
7 P-值与假设检验 但是,应注意以下两点 但是,应注意以下两点:: 如果H 为真,则对于连续的x ,P 在[0,1]范围内均匀分布. G ¾在P-值定义中不涉及别的假设。 根据P-值的定义,对 H 假设拟合优度的检验可以通过计算P-值的大小 来完成。 ¾P-值是一个随机变量。前面采用的显著水平在检验时已经被指定为常数。 如果H 非真,则P的概率密度函数通常很接近零

例子:拟合优度检验 投N次硬币,观察到h次头朝上的概率服从二项式分布: N! ,,)n-nD-p, 假设H:硬币是公平的(朝上的p%=朝下的p,=O.5) 取拟合优度检验统计量tn,-N/2| 投N=20次硬币,观察到17次头朝上,则ts17-20/2卡7 在t-空间中,具有相同或较少符合的区域为 t=(n-N/2)≥7 P-值=P(2=0,1,2,3,17,18,19,20)=∑f≈0.0026 i<8 8
8 例子:拟合优度检验 投 N 次硬币,观察到 nh 次头朝上的概率服从二项式分布: h N nh h n h h h h h p p n N n N f n p N − − − = (1 ) !( )! ! ( ; , ) 假设H:硬币是公平的(朝上的 ph = 朝下的 pt = 0.5) | / 2 | h t n = − N 投 N=20 次硬币,观察到17次头朝上,则 |17 20 / 2 | 7 obs t = − = 在 t-空间中,具有相同或较少符合的区域为 8 ( / 2) 7 ( 0,1, 2,3,17,18,19, 20) 0.0026 h h i i t n N P P n f ≤ = − ≥ − = 值 = = ∑ ≈ 取拟合优度检验统计量

拟合优度检验中的问题 问题:当P值等于0.0026,是否意味着H假设是错的? P值并不回答此问题。它只是给出与观察到的结果一样, 与H假设不符或者高于H假设(pp,=0.5)的概率。 P值=“偶然”得到如此奇怪结果的概率 种实用的检验方法是在同样的假设下,产生同 样数目的事例足够多次。检查如此奇怪的结果发 生的概率是否与P值相当。 9
9 拟合优度检验中的问题 问题:当 P -值等于0.0026,是否意味着 H 假设是错的? P -值并不回答此问题。它只是给出与观察到的结果一样, 与 H 假设不符或者高于 H 假设( p h =pt=0.5 )的概率。 P - 值=“偶然 ”得到如此奇怪结果的概率 一种实用的检验方法是在同样的假设下,产生同 样数目的事例足够多次。检查如此奇怪的结果发 生的概率是否与 P -值相当。 一种实用的检验方法是在同样的假设下,产生同 样数目的事例足够多次。检查如此奇怪的结果发 生的概率是否与 P -值相当

观测到一个信号的显著程度 假设观测n个事例,包含了 n,=已知过程(或本底)的事例数 n,=新过程(或信号)的事例数 如果n,n,服从泊松分布,均值为'。,它们之和n=n+n,也是 服从泊松分布,均值为v=V。+V,: P(n:vs,V)= y,+,)'e+w) n. 如果⅓=0.5而且观测到nobs=5 可否就此声称该迹象为新的发现? 假设H:y=0,即只有本底过程出现。 也就是所谓的“无效假设” 10
10 观测到一个信号的显著程度 假设观测 n 个事例,包含了 n b =已知过程 (或本底 )的事例数 ( ) ! ( ) ( ; , ) s b e n P n n s b s b ν ν ν ν ν ν + − + = 如果 νs =0.5而且观测到 nobs = 5 可否就此声称该迹象为新的发现? 可否就此声称该迹象为新的发现? 假设 H:νs=0,即只有本底过程出现。 n s =新过程 (或信号 )的事例数 b s b s b s b s n n ν ν n n n ν ν ν = + = + 如果 , 服从泊松分布,均值为 , ,它们之和 也是 服从泊松分布,均值为 : 也就是所谓的“无效假设” 也就是所谓的“无效假设