
粒子物理与核物理实验中的数 据分析 陈少敏 清华大学 第三讲:蒙特卡罗方法 http://hep.tsinghua.edu.cn/~chensm/lectures/lecture 3.pdf
粒子物理与核物理实验中的数 据分析 陈少敏 清华大学 第三讲 :蒙特卡罗方法 http://hep.tsinghua.edu.cn/~chensm/lectures/lecture_3.pdf

本讲要点 蒙特卡罗方法 ■随机数产生子 ■任意分布抽样之函数变换法与舍选法 蒙特卡罗方法中的精度问题 ■在粒子与核物理中的应用
本讲要点 蒙特卡罗方法 随机数产生子 任意分布抽样之函数变换法与舍选法 蒙特卡罗方法中的精度问题 在粒子与核物理中的应用

蒙特卡罗方法简介 蒙特卡罗方法就是利用一系列随机数来计算各种概率和相关 量的数值分析技术。通常的步骤为: 1)产生一系列在[0,1]之间均匀分布的随机数,,,'m。 2) 利用这些随机数按某些概率密度函数∫(x)抽样生成我 们感兴趣的另一随机序列x,x2,,X,0 3) 利用这些x值来估计∫(x)的一些特性,例如:通过找 到在区间a≤x≤b的x比例, 给出积分值fx)dk。 第一层面上的应用: 蒙特卡罗计算=积分 第二层面上的应用: 蒙特卡罗变量=“模拟的数据
蒙特卡罗方法简介 蒙特卡罗方法就是利用一系列随机数来计算各种概率和相关 量的数值分析技术。通常的步骤为: 1) 产生一系列在[0,1]之间均匀分布的随机数 。 2) 利用这些随机数按某些概率密度函数 抽样生成我 们感兴趣的另一随机序列 。 3) 利用这些 值来估计 的一些特性,例如:通过找 到在区间 的 比例,给出积分值 。 m r ,r ,..., r 1 2 f ( x ) n x , x ,..., x 1 2 x x f ( x ) a ≤ x ≤ b ∫ b a f ( x )dx 第一层面上的应用: 蒙特卡罗计算 = 积分 第二层面上的应用: 蒙特卡罗变量 = “模拟的数据
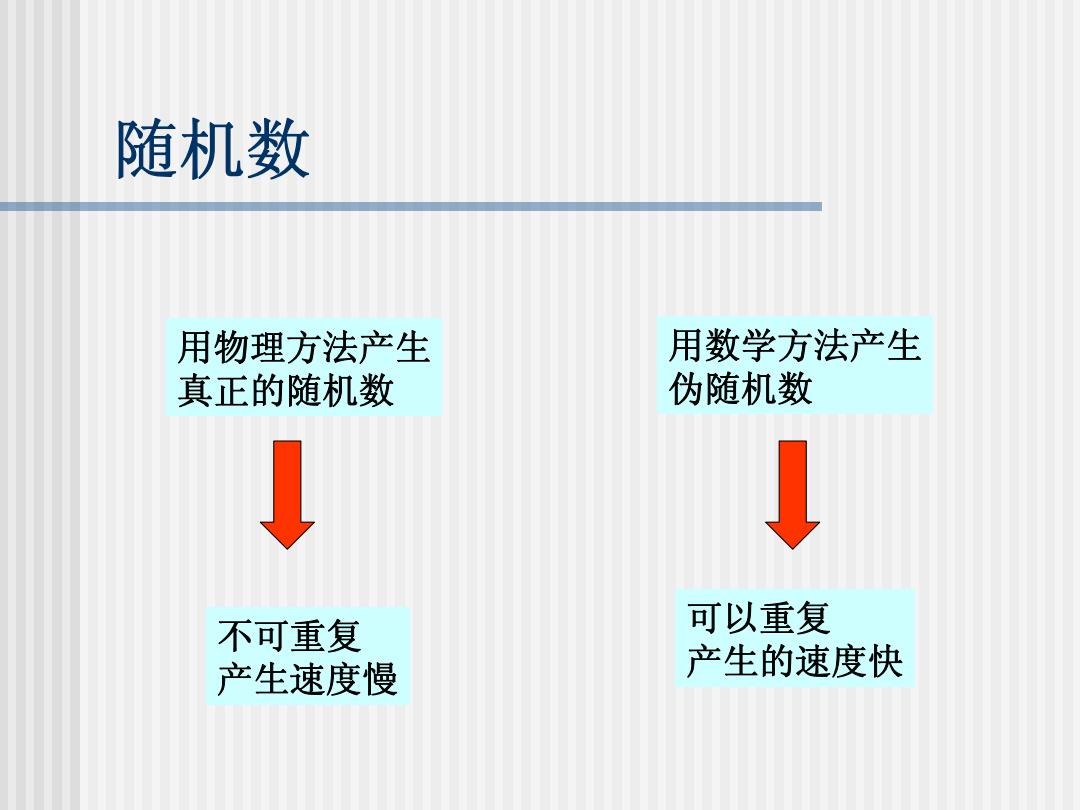
随机数 用物理方法产生 用数学方法产生 真正的随机数 伪随机数 不可重复 可以重复 产生速度慢 产生的速度快
随机数 用物理方法产生 真正的随机数 不可重复 产生速度慢 用数学方法产生 伪随机数 可以重复 产生的速度快
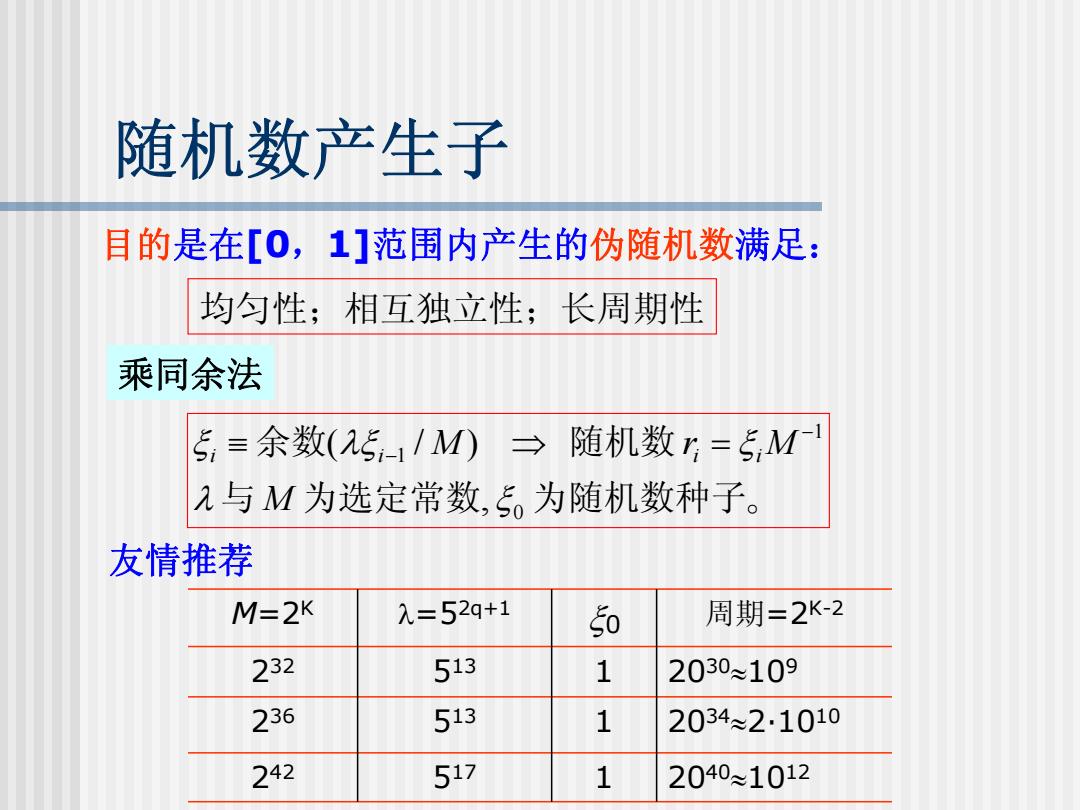
随机数产生子 目的是在[0,1]范围内产生的伪随机数满足: 均匀性;相互独立性;长周期性 乘同余法 5=余数(5,-1/M)→随机数5=5M 入与M为选定常数,5。为随机数种子。 友情推荐 M=2K λ=52q+1 50 周期=2K-2 232 513 1 2030≈109 236 53 1 2034≈2.1010 242 517 1 2040≈1012
随机数产生子 目的是在[0 ,1]范围内产生的伪随机数满足: 均匀性;相互独立性;长周期性 乘同余法 , 。 ( / ) 0 1 1 与 为选定常数 为随机数种子 余数 随机数 λ ξ ξ λξ ξ M i i M ri i M − ≡ − ⇒ = 友情推荐 M=2 K λ=52q+1 ξ0 周期=2K-2 232 513 1 2030 ≈10 9 236 513 1 2034 ≈2·1010 242 517 1 2040 ≈1012

CERN库的随机数产生子 PAW用户 Real random(1) Call Rmarin(ISEED,0,0) 注意:用于产生子的 Call Ranmar(random,1) 随机数种子还可以用 来保证后续进程的随 Root用户 机数不重复。 gRandom->SetSeedO; 粒子物理与核物理 研究中,大都采用 Float t random gRandom->Rndm(1); CERN程序库提供 的随机数产生子
CERN库的随机数产生子 PAW用户 … gRandom->SetSeed(); … Float_t random = gRandom->Rndm(1); … … Real random(1) Call Rmarin(ISEED,0,0) … Call Ranmar(random,1) … 注意: 用于产生子的 随机数种子还可以用 来保证后续进程的随 Root 用户 机数不重复。 粒子物理与核物理 研究中,大都采用 CERN程序库提供 的随机数产生子。 粒子物理与核物理 研究中,大都采用 CERN程序库提供 的随机数产生子
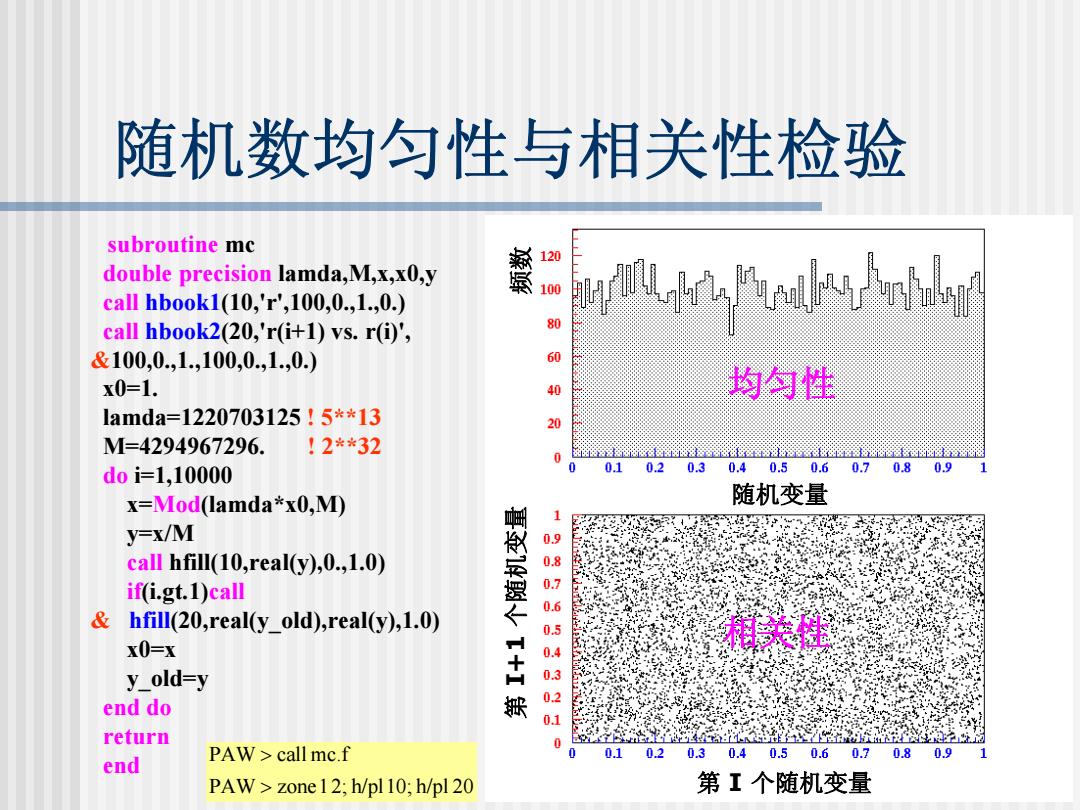
随机数均匀性与相关性检验 subroutine mc 120 double precision lamda,M,x,x0,y 100 call hbook1(10,'r',100,0.,1.,0.) call hbook2(20,'r(i+1)vs.r(i)', 80 &100,0.,1.,100,0,1.,0.) 60 x0=1. 40 均匀性 lamda=1220703125!5*13 20 M=4294967296. !2*32 doi=1,10000 0.1 0.2 0.3 0.40.50.60.7 0.80.9 x=Mod(lamda*x0,M) 随机变量 y=x/M call hfill(10,real(y),0.,1.0) if(i.gt.1)call & hfill(20,real(y_old),real(y),1.0) x0=x y_old=y N财654女 end do return 0 PAW>call mc.f 01 0.2 0.30.4 0.50.6 0.70.80.9 end PAW zone 12;h/pl 10;h/pl 20 第I个随机变量
随机数均匀性与相关性检验 subroutine mc dou ble precision lamda,M,x,x0,y call hbook 1(10,'r',100,0.,1.,0.) call hbook 2(20,'r(i+1) vs. r(i)', &100,0.,1.,100,0.,1.,0.) x0=1. lamda=1220703125 ! 5**13 M=4294967296. ! 2**32 do i=1,10000 x=Mod(lamda*x0,M) y=x/M call hfill(10,real(y),0.,1.0) if(i.gt.1)call & hfill(20,real(y_old),real(y),1.0) x0= x y_old=y end do return end 随机变量 第 I 个随机变量 第 I+1 个随机变量 频数 均匀性 相关性 PAW zone12; h/pl10; h/pl 20 PAW call mc.f > >
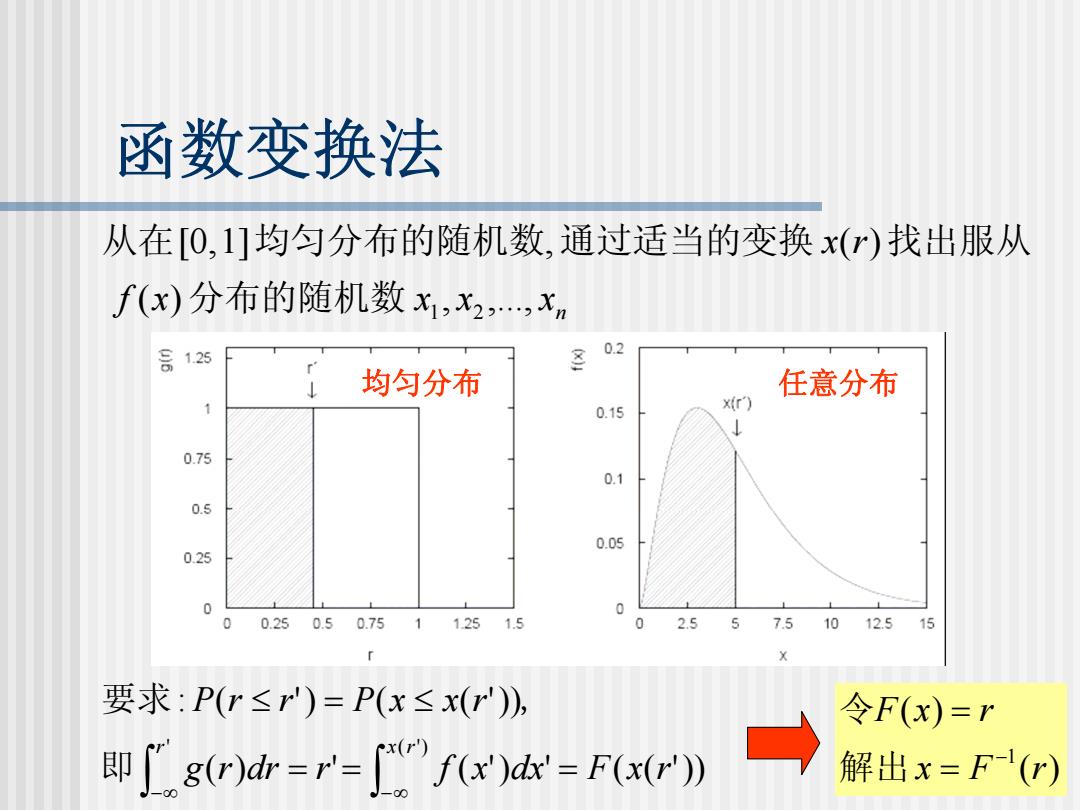
函数变换法 从在[O,1]均匀分布的随机数,通过适当的变换x(r)找出服从 f(x)分布的随机数x,x2,,xm 1.25 02 均匀分布 任意分布 1 0.15 x(r) 0.75 0.1 0.5 0.05 0.25 0 0.25 0.50.7511251.5 0 2.55 7.510 12.5 15 要求:P(r≤r)=P(x≤x(r), 令F(x)=r 即'gr)dr=r=f(x)a=F(xr》 解出x=F(r)
函数变换法 n f x x x x x r ( ) , ,..., [0,1] , ( ) 分布的随机数 1 2 从在 均匀分布的随机数 通过适当的变换 找出服从 ∫ ∫ − ∞ ∞ − = = = ≤ = ≤ ' ) ( ' ( ) ' ( ') ' ( ( ')) : ( ') ( ( ')), r r x g r dr r f x dx F x r P r r P x x r 即 要求 ( ) ( ) 1 x F r F x r − = = 解出 令 均匀分布 任意分布
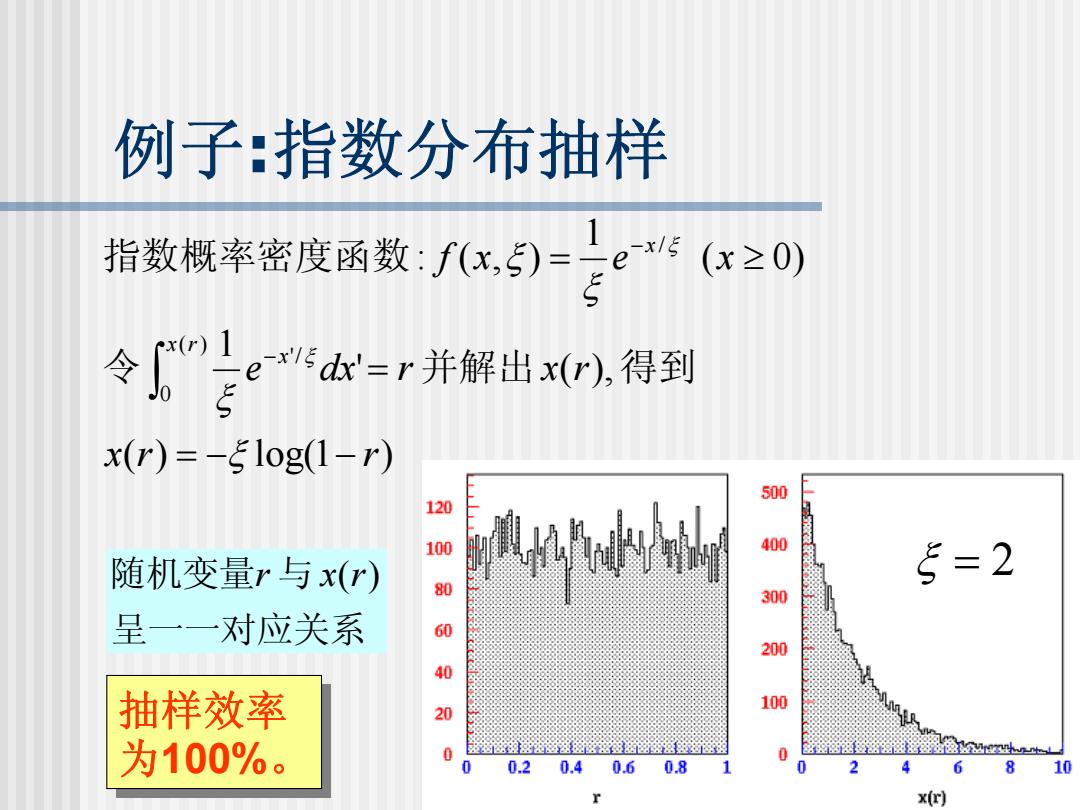
例子:指数分布抽样 指数慨率密度函数5)-e (x≥0) 令e-r并解出.符到 5 x(r)=-51og(1-r) 500 120 100 400 随机变量r与x(r) 5=2 80 300 呈一一对应关系 60 200 40 抽样效率 20 100 为100%。 0 密湿密密区密蜜☒密落 0 0 0.2 0.4 0.6 0.8 1 2 8 10 x(r)
例子:指数分布抽样 ( ) log(1 ) ' ( ), 1 ( 0) 1 : ( , ) ( ) 0 '/ / x r r e dx r x r f x e x x r x x = − − = = ≥ ∫ − − ξ ξ ξ ξ ξ ξ 令 并解出 得到 指数概率密度函数 ξ = 2 呈一一对应关系 随机变量r 与 x(r) 抽样效率 为100%。 抽样效率 为100%
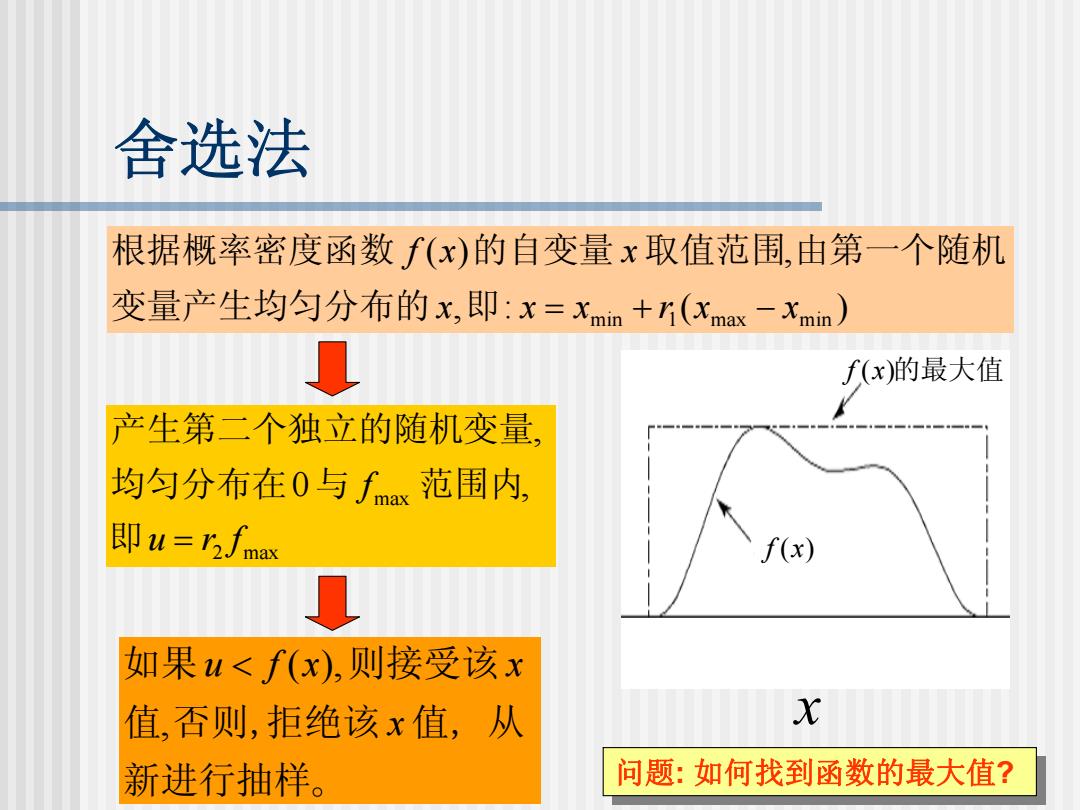
舍选法 根据概率密度函数f(x)的自变量x取值范围,由第一个随机 变量产生均匀分布的x,即:x=xmin+h(xmax一xmin) f(x)的最大值 产生第二个独立的随机变量, 均匀分布在0与fx范围内, 即l=乃2∫max f(x) 如果u<f(x),则接受该x 值,否则,拒绝该x值,从 X 新进行抽样。 问题:如何找到函数的最大值?
舍选法 , : ( ) ( ) , min 1 max min x x x r x x f x x 变量产生均匀分布的 即 = + − 根据概率密度函数 的自变量 取值范围 由第一个随机 2 max max 0 , , u r f f 即 = 均匀分布在 与 范围内 产生第二个独立的随机变量 。 , , , ( ), 新进行抽样 值 否则 拒绝该 值 从 如果 则接受该 x u < f x x 问题问题: : 如何找到函数的最大值 如何找到函数的最大值?? x f (x)的最大值 f (x)