
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第十三讲:盲分析方法
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第十三讲:盲分析方法

本讲要点 ■什么是盲分析方法? ■为什么要用盲分析方法? ■几种日前采用的盲分析方法 ■应用举例 ■评论 2
2 本讲要点 什么是盲分析方法? 为什么要用盲分析方法? 几种目前采用的盲分析方法 应用举例 评论

什么是盲分析方法? >盲分析方法是一种不以预期答案为参照系而进行的实验测量过程。 >最早提出于寻找粒子物理里的稀有物理过程实验研究中。 定义的信号区间 所有数据分析均在信号区外进行 所有数据 >至今为止,盲分析方法已经发展为各自有不同特点的几大类。 3
3 什么是盲分析方法 ? ¾盲分析方法是一种不以预期答案为参照系而进行的实验测量过程。 ¾最早提出于寻找粒子物理里的稀有物理过程实验研究中。 所有数据 定义的信号区间 所有数据分析均在信号区外进行 ¾至今为止,盲分析方法已经发展为各自有不同特点的几大类
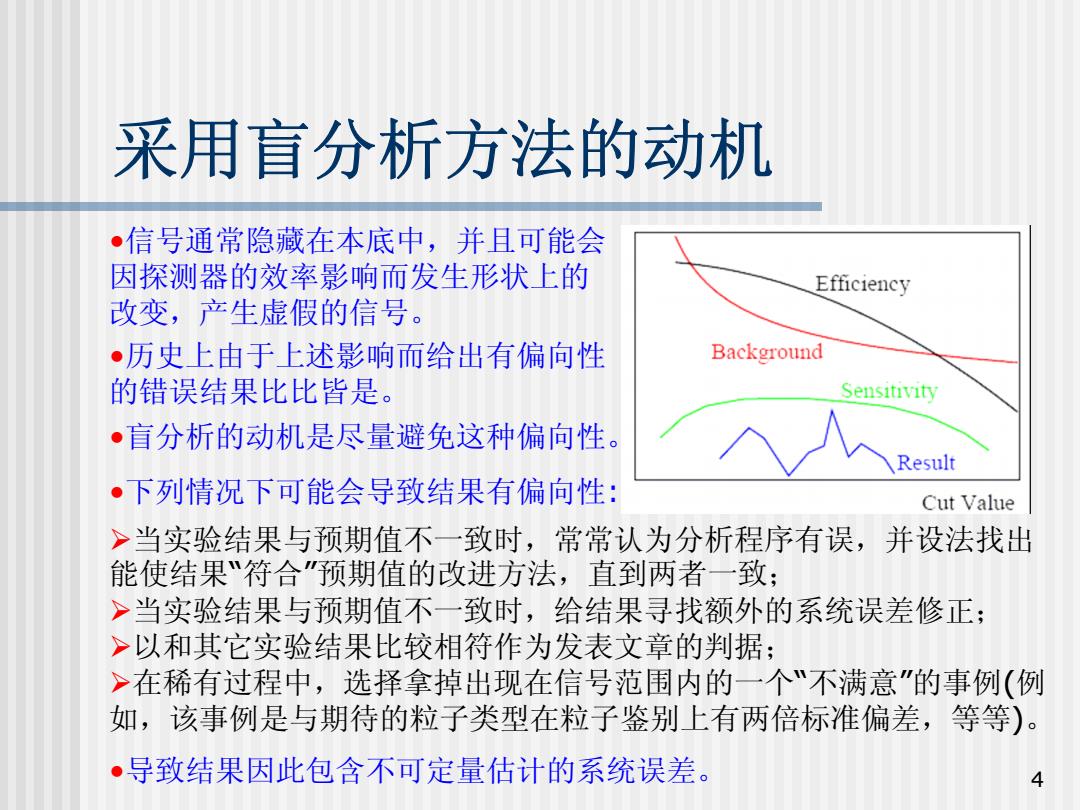
采用盲分析方法的动机 •信号通常隐藏在本底中,并且可能会 因探测器的效率影响而发生形状上的 Efficiency 改变,产生虚假的信号。 •历史上由于上述影响而给出有偏向性 Background 的错误结果比比皆是。 Sensitivity ·盲分析的动机是尽量避免这种偏向性。 Result ·下列情况下可能会导致结果有偏向性: Cut Value >当实验结果与预期值不一致时,常常认为分析程序有误,并设法找出 能使结果“符合"预期值的改进方法,直到两者一致: >当实验结果与预期值不一致时,给结果寻找额外的系统误差修正; >以和其它实验结果比较相符作为发表文章的判据: >在稀有过程中,选择拿掉出现在信号范围内的一个“不满意”的事例(例 如,该事例是与期待的粒子类型在粒子鉴别上有两倍标准偏差,等等)。 导致结果因此包含不可定量估计的系统误差。 4
4 采用盲分析方法的动机 •盲分析的动机是尽量避免这种偏向性。 •下列情况下可能会导致结果有偏向性: ¾当实验结果与预期值不一致时,常常认为分析程序有误,并设法找出 能使结果 “符合 ”预期值的改进方法,直到两者一致; ¾当实验结果与预期值不一致时,给结果寻找额外的系统误差修正; ¾以和其它实验结果比较相符作为发表文章的判据; ¾在稀有过程中,选择拿掉出现在信号范围内的一个 “不满意 ”的事例 ( 例 如,该事例是与期待的粒子类型在粒子鉴别上有两倍标准偏差,等等 )。 •导致结果因此包含不可定量估计的系统误差。 •信号通常隐藏在本底中,并且可能会 因探测器的效率影响而发生形状上的 改变,产生虚假的信号。 •历史上由于上述影响而给出有偏向性 的错误结果比比皆是
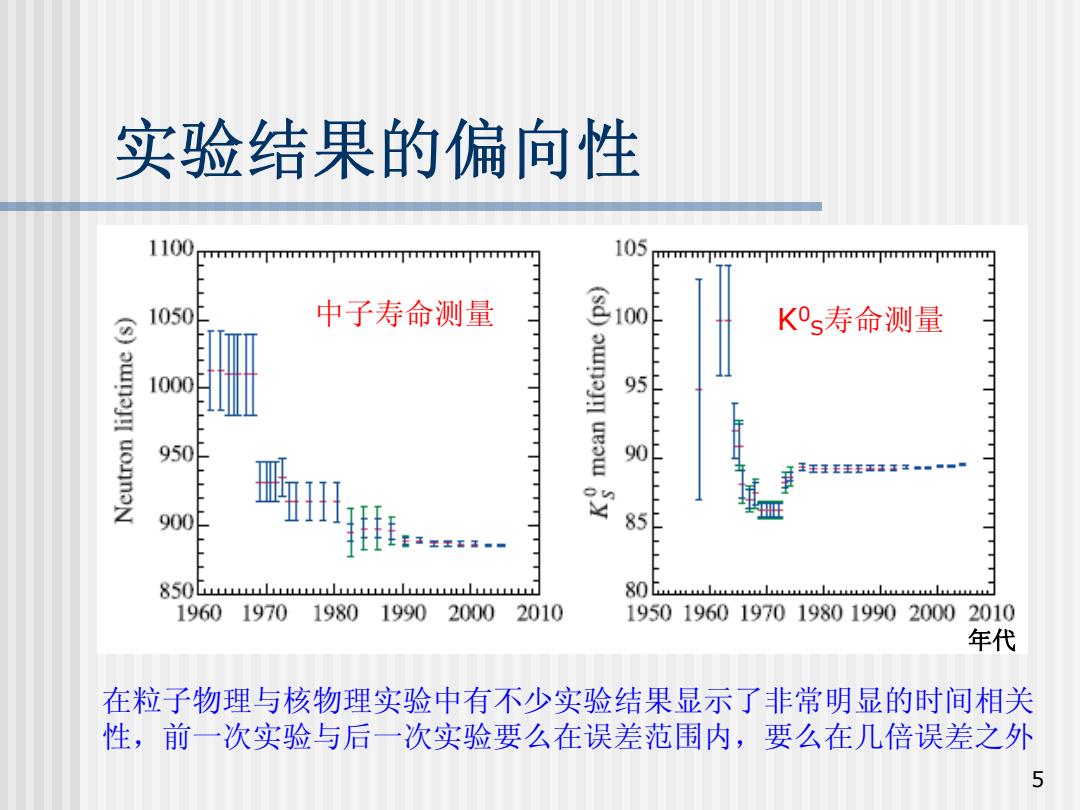
实验结果的偏向性 1100 105 1050 中子寿命测量 100 Ks寿命测量 1000 95 950 90 900 85 80 1960 19701980 19902000 2010 1950196019701980199020002010 年代 在粒子物理与核物理实验中有不少实验结果显示了非常明显的时间相关 性,前一次实验与后一次实验要么在误差范围内,要么在几倍误差之外 5
5 实验结果的偏向性 在粒子物理与核物理实验中有不少实验结果显示了非常明显的时间相关 性,前一次实验与后一次实验要么在误差范围内,要么在几倍误差之外 年代 中子寿命测量 K 0 S寿命测量
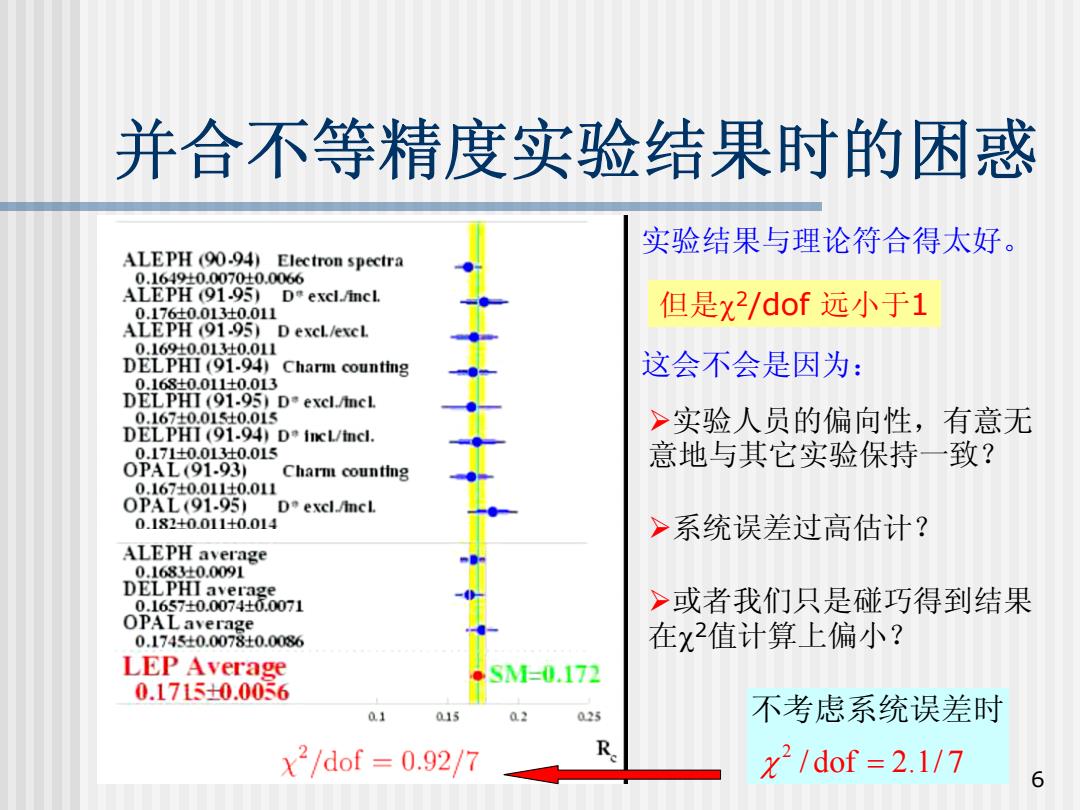
并合不等精度实验结果时的困惑 实验结果与理论符合得太好。 ALEPH (90.94)Electron spectra 0.164910.0070吐0.0066 ALEPH (91-95)D*excl./incL 0.176±0.01340.011 但是x2/dof远小于1 ALEPH (91-95)D excL/excL 0.1690.013±0.011 DELPHI (91-94)Charm counting 这会不会是因为: 0.168±0.011±0.013 DELPHI(91-95)D"excl./ineL 0.1670.015±0.015 DELPHI (91-94)D*incL/tnel. >实验人员的偏向性,有意无 0.171±0.0130.015 意地与其它实验保持一致? 0PAL(91.93) Charm counting 0.167±0.011±0.011 OPAL(91-95)D"excl./mcL 0.182+0.011±0.014 >系统误差过高估计? ALEPH average 0.1683±0.0091 DELPHI average 0.1657±0.0074±0.0071 >或者我们只是碰巧得到结果 OPALaverage 0.1745±0.0078±0.0086 在x2值计算上偏小? LEP Average SMi=0.172 0.1715±0.0056 015 023 不考虑系统误差时 x2/dof=0.92/7 x21dof=2.1/7 6
6 并合不等精度实验结果时的困惑 实验结果与理论符合得太好。 这会不会是因为: ¾实验人员的偏向性,有意无 意地与其它实验保持一致? ¾系统误差过高估计? ¾或者我们只是碰巧得到结果 在 χ 2值计算上偏小? 但是 χ 2/dof 远小于 1 2 χ / dof = 2.1 / 7 不考虑系统误差时
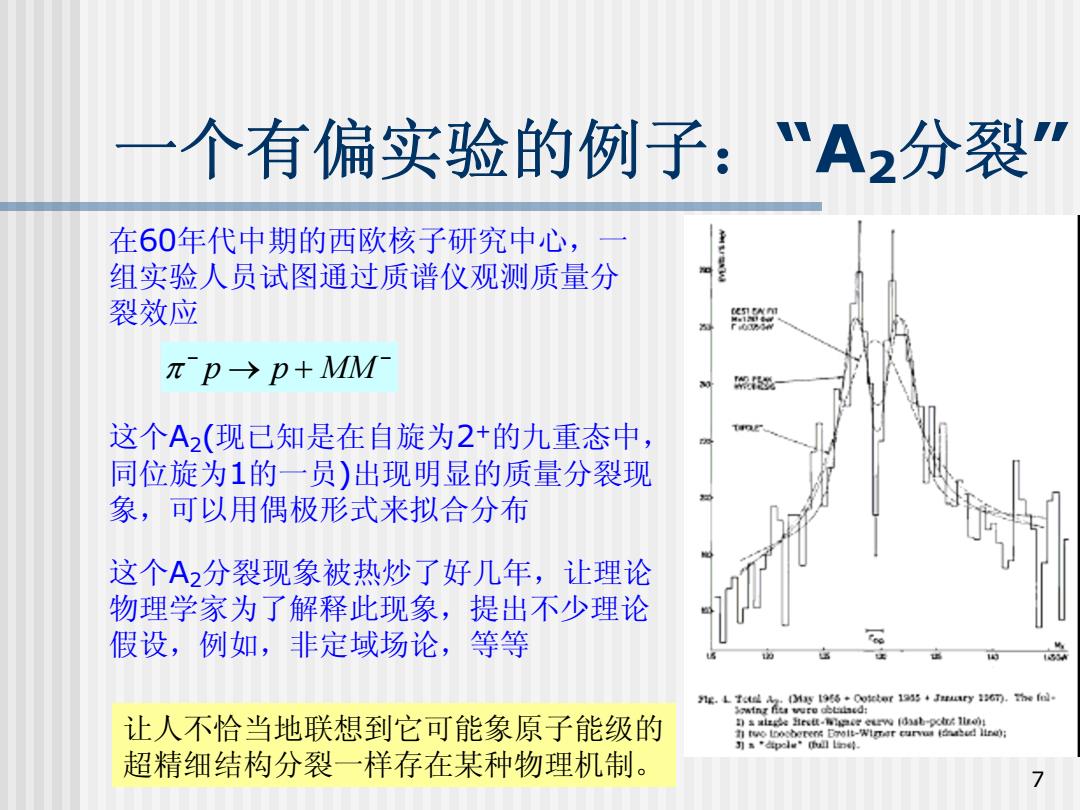
一个有偏实验的例子:"A2分裂” 在60年代中期的西欧核子研究中心, 组实验人员试图通过质谱仪观测质量分 裂效应 πp→p+MM 这个A2(现已知是在自旋为2+的九重态中, 同位旋为1的一员)出现明显的质量分裂现 象,可以用偶极形式来拟合分布 这个A2分裂现象被热炒了好几年,让理论 物理学家为了解释此现象,提出不少理论 假设,例如,非定域场论,等等 wing ft vuro o企aed: 让人不恰当地联想到它可能象原子能级的 目s alngbe Hrvtt-49 ce eurw idab-g在k1lne0: 3月s”2le”国n4 超精细结构分裂一样存在某种物理机制
7 一个有偏实验的例子:“A 2分裂 ” 在60年代中期的西欧核子研究中心,一 组实验人员试图通过质谱仪观测质量分 裂效应 π p p MM − − → + 这个 A 2 (现已知是在自旋为 2 +的九重态中, 同位旋为 1的一员 )出现明显的质量分裂现 象,可以用偶极形式来拟合分布 这个 A 2分裂现象被热炒了好几年,让理论 物理学家为了解释此现象,提出不少理论 假设,例如,非定域场论,等等 让人不恰当地联想到它可能象原子能级的 超精细结构分裂一样存在某种物理机制

A2分裂”例子(续) 但是,此后类似的几个实验均未发现任何这种质量分裂效应 另外一些别的实验通过A)衰变到不同的K+K模式,也没有发现任何质量 分裂的现象 最后在1971年华盛顿美国物理学会年会上,该实验的发言人宣布所观测 到的质量分裂结果是由几个没有必要的事例选择条件人为造成的 其中的一个选择条件是与实验运行条件"有关。当拿掉该选择条件以后, 再也看不到质量分裂效应了 这个例子被广泛任为是“无辜偏向性“的受害者 在粒子物理与核物理实验研究中,历史上类似的无辜偏向性“受害者 很多。为了避免这种情况的发生,近几年来盲分析方法渐渐成为潮流。 8
8 “A2分裂”例子(续) 但是,此后类似的几个实验均未发现任何这种质量分裂效应 另外一些别的实验通过A2衰变到不同的K+K-模式,也没有发现任何质量 分裂的现象 最后在1971年华盛顿美国物理学会年会上,该实验的发言人宣布所观测 到的质量分裂结果是由几个没有必要的事例选择条件人为造成的 其中的一个选择条件是与“实验运行条件”有关。当拿掉该选择条件以后, 再也看不到质量分裂效应了 这个例子被广泛任为是“无辜偏向性”的受害者 在粒子物理与核物理实验研究中,历史上类似的“无辜偏向性”受害者 很多。为了避免这种情况的发生,近几年来盲分析方法渐渐成为潮流

盲分析方法分类 信号区隐藏法 •最适合于对稀有或禁戒物理过程的实验测量; ·本底必须从非信号区、或模拟样本、或额外的子实验来估计。 偏置法 •适合于单值测量(例如,测量不对称性),而且, 统计误差已经不是 实验上的决定因素; •拟合量中包含随机的符号与偏置: 分解法 •将实验分解为对若干个子测量量的研究而不看最终结果; ·最终结果为各不同子测量量的计算总汇(例如,μ-子磁矩测量中, 分别测量μ-子的进动频率与回旋频率差和磁场大小,最后得到子 磁矩的测量值) 9
9 盲分析方法分类 信号区隐藏法 偏置法 分解法 •最适合于对稀有或禁戒物理过程的实验测量; •本底必须从非信号区、或模拟样本、或额外的子实验来估计。 •适合于单值测量 (例如,测量不对称性 ),而且,统计误差已经不是 实验上的决定因素; •拟合量中包含随机的符号与偏置; •将实验分解为对若干个子测量量的研究而不看最终结果; •最终结果为各不同子测量量的计算总汇 (例如, μ -子磁矩测量中, 分别测量 μ -子的进动频率与回旋频率差和磁场大小,最后得到 μ - 子 磁矩的测量值 )

盲分析方法分类 信号强度变化法 •添加随机数目的信号事例数; ·可以默认蒙特卡罗模拟的信号非常可靠; ·也可利用与信号非常相似,但已知为本底的事例。 样本分流法 ·将样本按一定比例分流为公开与非公开两部分; ·对若干比例(例如,总数据量的10%)的公开样本进行正常分析; •将分析程序固定不变,分析非公开样本,最后的结果只依赖于 非公开样本(例如,另外90%的数据)。 方法的采用完全取决于实际测量量的特点。 10
10 盲分析方法分类 信号强度变化法 样本分流法 •添加随机数目的信号事例数; •可以默认蒙特卡罗模拟的信号非常可靠; •也可利用与信号非常相似,但已知为本底的事例。 •将样本按一定比例分流为公开与非公开两部分; •对若干比例 (例如,总数据量的10%)的公开样本进行正常分析; •将分析程序固定不变,分析非公开样本,最后的结果只依赖于 非公开样本 (例如,另外90%的数据 )。 方法的采用完全取决于实际测量量的特点