
振动是一种普遍的运动形式 机械振动:物体在某固定位置附近的往复运动, 是物体一种普遍的运动形式 广义振动:任何一个物理量在某一量值附近随 时间作周期性变化. 振动分类 受迫振动 共振 振动 (自由振动 阻尼自由振动 无阻尼自由非谐振动 无阻尼自由振动 无阻尼自由谐振动 (简谐振动)
------------------------------------------------------------------------------- 振动是一种普遍的运动形式 机械振动: 物体在某固定位置附近的往复运动, 是物体一种普遍的运动形式 . 广义振动:任何一个物理量在某一量值附近随 时间作周期性变化. 振动分类 振动 受迫振动 自由振动 共振 阻尼自由振动 无阻尼自由振动 无阻尼自由非谐振动 无阻尼自由谐振动 (简谐振动)

§10.1简谐振动的动力学特征 振动中最简单最基本的是简谐振动 简谐振动: 一个做往复运动的物体,如果其偏离平衡位置 的位移x(或角位移0随时间按余弦(或正弦)规律变 化的振动 x=Acos(@t+go) 运动学方程 x可作广义理解: 位移、电流、场强、温度. 雨的南网
------------------------------------------------------------------------------- §10.1 简谐振动的动力学特征 振动中最简单最基本的是简谐振动 简谐振动: 一个做往复运动的物体,如果其偏离平衡位置 的位移x(或角位移)随时间t按余弦(或正弦)规律变 化的振动 x=Acos(t+0 ) 运动学方程 x 可作广义理解: 位移、电流、场强、温度…
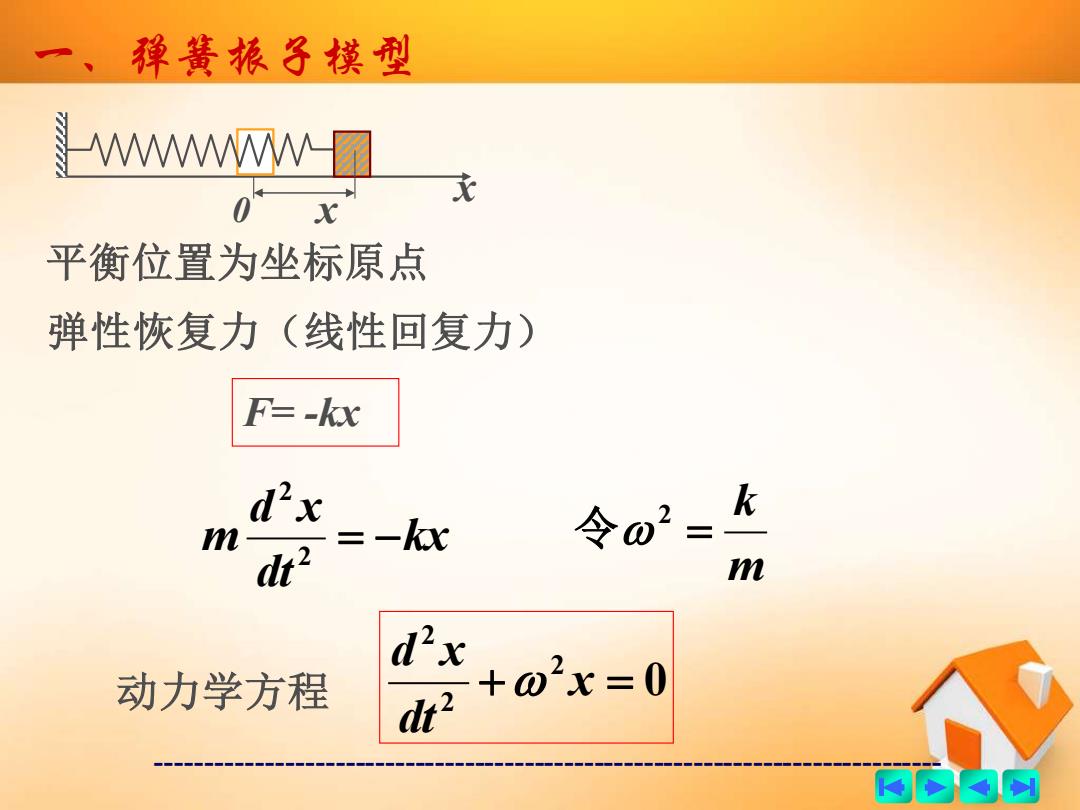
一、弹簧振子模型 WWWW-圈 平衡位置为坐标原点 弹性恢复力(线性回复力) F=-kx d2x 令02= k n =- m d2x 动力学方程 2+o2x=0 商的内网
------------------------------------------------------------------------------- x 0 x 一、弹簧振子模型 平衡位置为坐标原点 弹性恢复力(线性回复力) F= -kx kx dt d x m = − 2 2 m k = 2 令 动力学方程 0 2 2 2 + x = dt d x
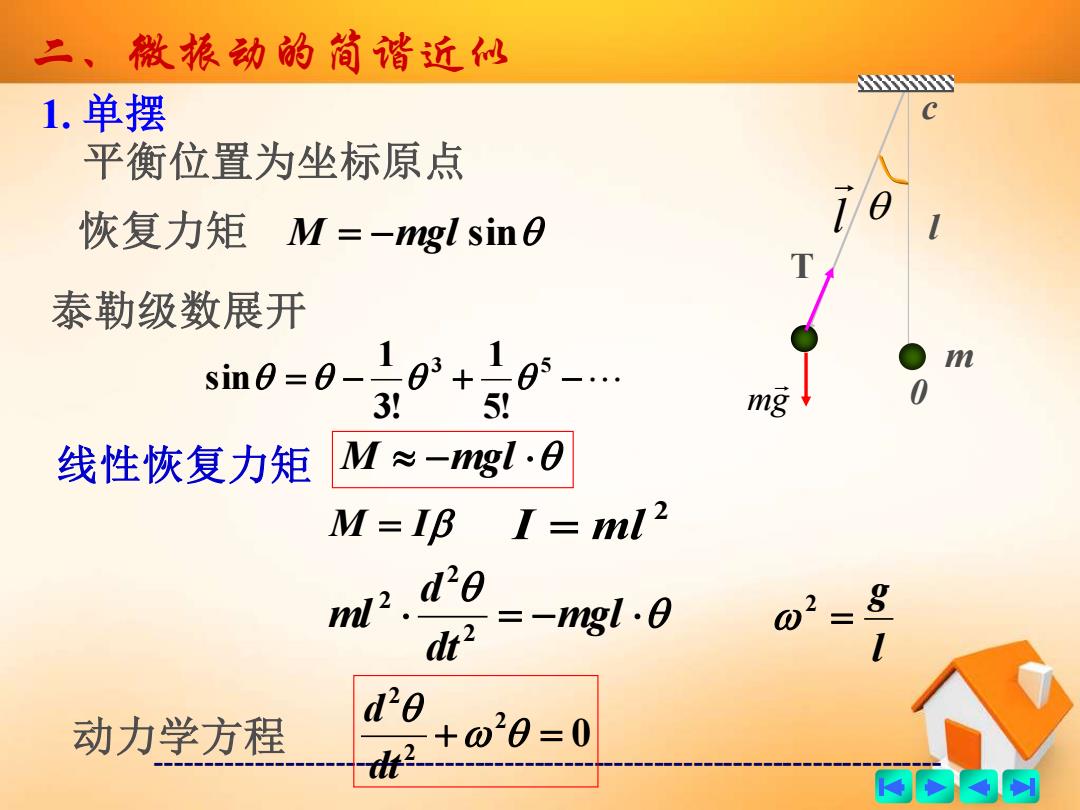
二、微振动的简谐近仙 S 1.单摆 平衡位置为坐标原点 恢复力矩M=-ngl sin0 泰勒级数展开 sin0=-10+9-… m 3! 5 mg 0 线性恢复力矩 M≈-gl.B M=I8 I=ml2 w2.120 =-g10 02 8 d20 动力学方程 +020=0 的南厨
------------------------------------------------------------------------------- 二、微振动的简谐近似 1. 单摆 c 0 mg l m T l 平衡位置为坐标原点 恢复力矩 M = −mgl sin 泰勒级数展开 = − 3 + 5 − 5! 1 3! 1 sin 线性恢复力矩 M −mgl M = I 2 I = ml = −mgl dt d ml 2 2 2 l g = 2 动力学方程 0 2 2 2 + = dt d
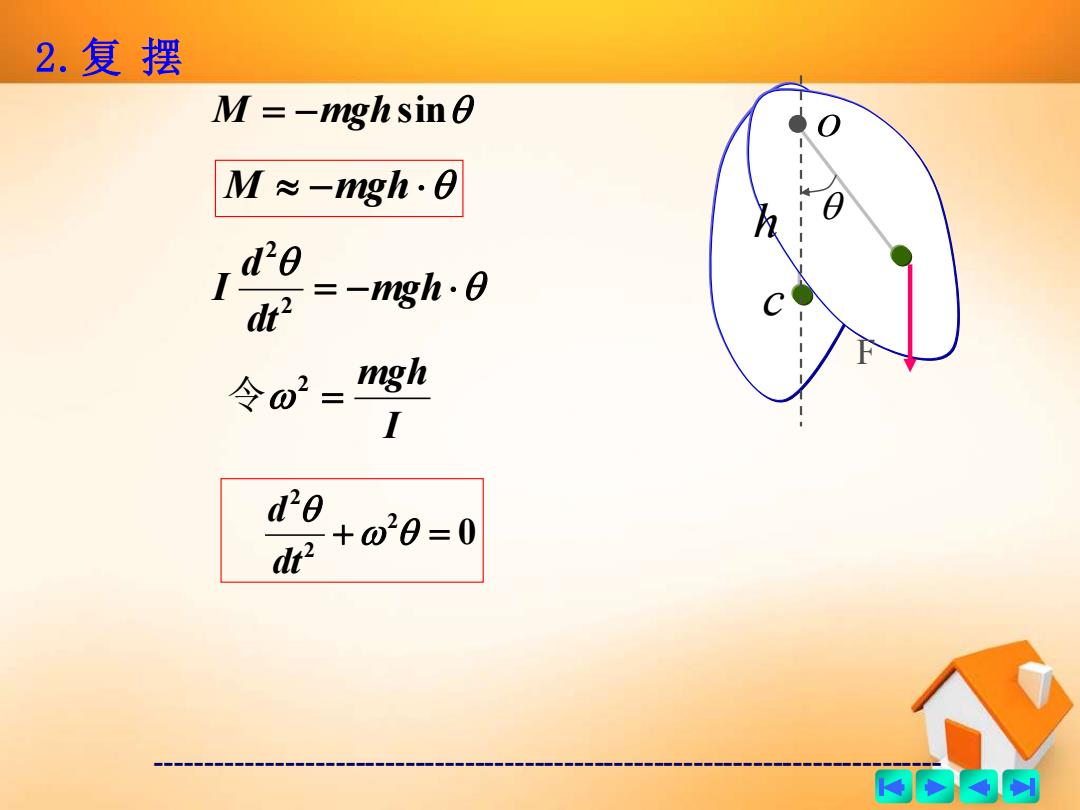
2.复摆 M=-mgh sin0 M≈-gh·B 牌g 令o2= mgh de d +020=0 商的内网
------------------------------------------------------------------------------- 2.复 摆 F c o h M = −mghsin M −mgh = −mgh dt d I 2 2 I mgh = 2 令 0 2 2 2 + = dt d
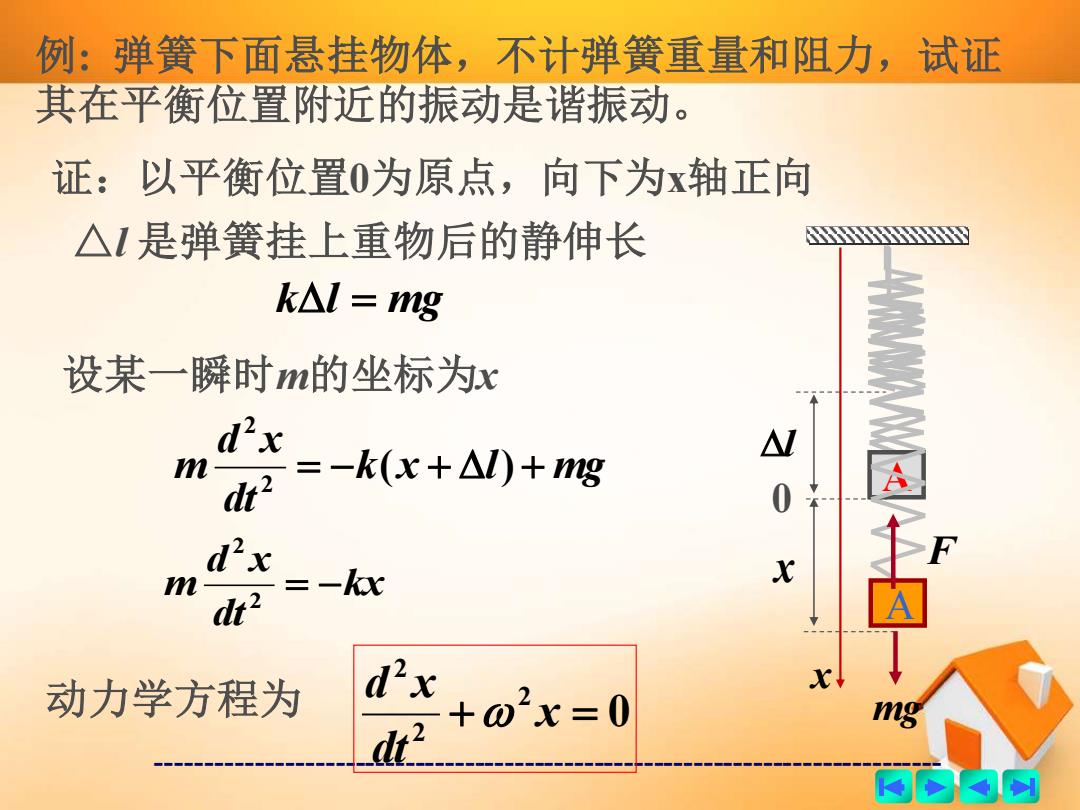
例:弹簧下面悬挂物体,不计弹簧重量和阻力,试证 其在平衡位置附近的振动是谐振动。 证:以平衡位置0为原点,向下为x轴正向 △1是弹簧挂上重物后的静伸长 k△l=mg 设某一瞬时m的坐标为x dx dt2 =-k(x+△l)+g 0 d2x =-c 动力学方程为 d'x dr2 +o2x=0 mg 商的内网
------------------------------------------------------------------------------- 例: 弹簧下面悬挂物体,不计弹簧重量和阻力,试证 其在平衡位置附近的振动是谐振动。 A 证:以平衡位置0为原点,向下为x轴正向 x 0 l △l 是弹簧挂上重物后的静伸长 kl = mg 设某一瞬时m的坐标为x A x F mg k x l mg dt d x m = − ( + ) + 2 2 kx dt d x m = − 2 2 动力学方程为 0 2 2 2 + x = dt d x

§10.2简谐振动的运动学 一、简谐振动的运动学方程 微分方程 d'x +02x=0 运动学方程 x=Acos(@t+p) A、由初始条件所决定 x 1.速度 =-A@sin(@t+o) dt D=±0NA2-x2 2.加速度 Q=- =-Ao'cos(@t+o) dt 两的肉的
------------------------------------------------------------------------------- §10.2 简谐振动的运动学 一、简谐振动的运动学方程 0 2 2 2 + x = dt d x 微分方程 运动学方程 cos( ) = +0 x A t A、0 由初始条件所决定 1.速度 sin( ) = = − +0 A t dt dx 2 2 = A − x 2.加速度 cos( ) 0 2 = = −A t + dt d a a x 2 = −

二.描述谐振动的三个特征量 1.振幅A 由初始条件决定 xo=AcosPo t=0 合-1sap, 4= 2.周期T 完成一次完全振动所需的时间 x=Acos(at+o)=Acosl@(t+T)+oo] =Ac0s(ot+p+2π) 两的肉例
------------------------------------------------------------------------------- 二. 描述谐振动的三个特征量 1.振幅A 由初始条件决定 t=0 = − = 0 0 0 0 sin cos A x A 2 2 0 2 0 A = x + 2. 周期T 完成一次完全振动所需的时间 cos( ) = +0 x A t 0 = Acos (t +T)+ cos( 2 ) = A t +0 +

周期T: T 2π ) 1 频率 V= T 2元 圆频率:0=2rV 固有圆频率:仅由振动系统的力学性质所决定频率 固有圆频率 固有振动周期 k 2 弹簧振子 0= m T=2πk 单摆 0= T=2r】 g mgh 复摆 0=V T= mgh 两的肉的
------------------------------------------------------------------------------- 周期T: 2 T = 频率: 2 1 = = T 圆频率: = 2 固有圆频率:仅由振动系统的力学性质所决定频率 弹簧振子 固有圆频率 m k = 固有振动周期 k m T = 2 单摆 l g = g l T = 2 复摆 I mgh = mgh I T = 2

3.位相和初位相 ()能唯一确定系统运动状态,而又能反映其周期性 特征的的物理量 0=0t+p0 叫做位相,是描述系统的机械运动状态的物理量 (2)初位相:=0时的位相φo xo=Acosgo p0=g'(- (3)位相差 两振动位相之差 △0=P2-P1 当△02kπ,k=0,士1,士2.,两振动步调相同,称同相 和形阿
------------------------------------------------------------------------------- 3. 位相和初位相 (1) 能唯一确定系统运动状态,而又能反映其周期性 特征的的物理量 =t+ 0 叫做位相, 是描述系统的机械运动状态的物理量 (2)初位相: t=0时的位相0 = − = 0 0 0 0 sin cos A x A ( ) 0 1 0 0 x tg = − − (3)位相差 两振动位相之差 =2 −1 当=2k ,k=0,±1,±2…,两振动步调相同,称同相