
第9章 电磁感应与电磁场 §91电磁感应定律 b§9.2 动生电动势与感生电动势 §9.3 自感应与互感应 >§9.4 磁场能量 §9.5 麦克斯韦电磁场理论简介 南内网
------------------------------------------------------------------------------- 第9章 电磁感应与电磁场 §9.1 电磁感应定律 §9.2 动生电动势与感生电动势 §9.3 自感应与互感应 §9.4 磁场能量 §9.5 麦克斯韦电磁场理论简介

电磁感应定律的发现,进一步揭示了电与 磁之间的相互联系及转化规律. 麦克斯韦提出了“感生电场”和“位移电 流”两个假说,从而建立了完整的电磁场理 论体系—麦克斯韦方程组 本章主要研究电场和磁场相互激发的规律
------------------------------------------------------------------------------- 电磁感应定律的发现,进一步揭示了电与 磁之间的相互联系及转化规律. 麦克斯韦提出了“感生电场”和“位移电 流”两个假说,从而建立了完整的电磁场理 论体系——麦克斯韦方程组 本章主要研究电场和磁场相互激发的规律

§9.11 电磁感应的基本定律 一、电磁感应现象 1820年,奥斯特发现: 电流磁效应 电流 产生 磁场 产生 对称性→磁的电效应? 1831年,法拉第经过了十年不懈的探索,发现 电磁感应现象 商的内网
------------------------------------------------------------------------------- §9.1 电磁感应的基本定律 一、电磁感应现象 1820年,奥斯特发现: 电流磁效应 电 流 产 生 磁 场 对称性 → 磁的电效应? ? 1831年,法拉第 经过了十年不懈的探索,发现 电磁感应现象 产 生

1.产生感应电流五种情况: 变化着的电流; 线圈中变化着的磁场; 运动中的恒定电流; 运动着的磁铁; 在磁场中运动着的导体。 感应电流与原电流本身无关 而是与原电流的变化有关。 这种现象称为电磁感应 原因:线圈中磁通量发生改变 →导致产生感应电动势! 两的内例
------------------------------------------------------------------------------- 1. 产生感应电流五种情况: 变化着的电流; 线圈中变化着的磁场; 运动中的恒定电流; 运动着的磁铁; 在磁场中运动着的导体. 感应电流与原电流本身无关, 而是与原电流的变化有关。 ——这种现象称为电磁感应 原因 :线圈中磁通量发生改变 →导致产生感应电动势!
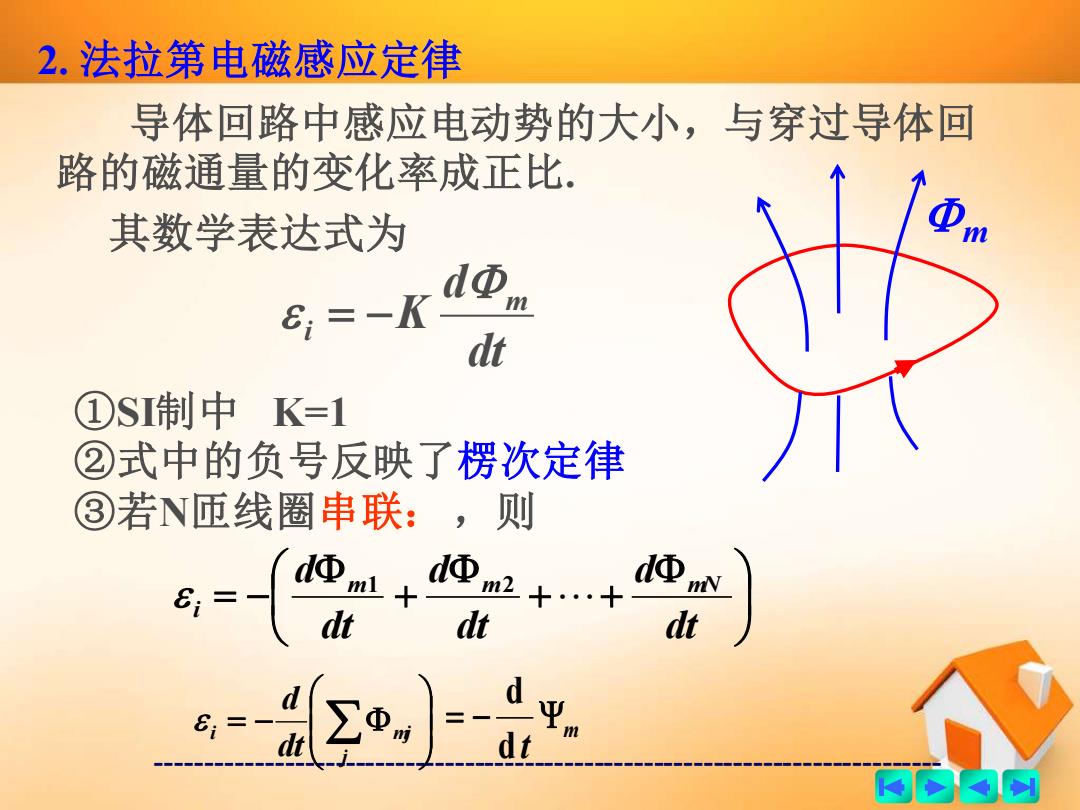
2.法拉第电磁感应定律 导体回路中感应电动势的大小,与穿过导体回 路的磁通量的变化率成正比, 其数学表达式为 6:=-K dΦm dt ①SI制中K=1 ②式中的负号反映了楞次定律 ③若N匝线圈串联:,则 ,= d n dt dΦm2+…+ dt dt d 商的内网
------------------------------------------------------------------------------- 导体回路中感应电动势的大小,与穿过导体回 路的磁通量的变化率成正比. 其数学表达式为 dt d K m i = − 2. 法拉第电磁感应定律 m ①SI制中 K=1 ②式中的负号反映了楞次定律 ③若N匝线圈串联: ,则 + + + = − dt d dt d dt d m m mN i 1 2 = − j i mj dt d m t = − d d
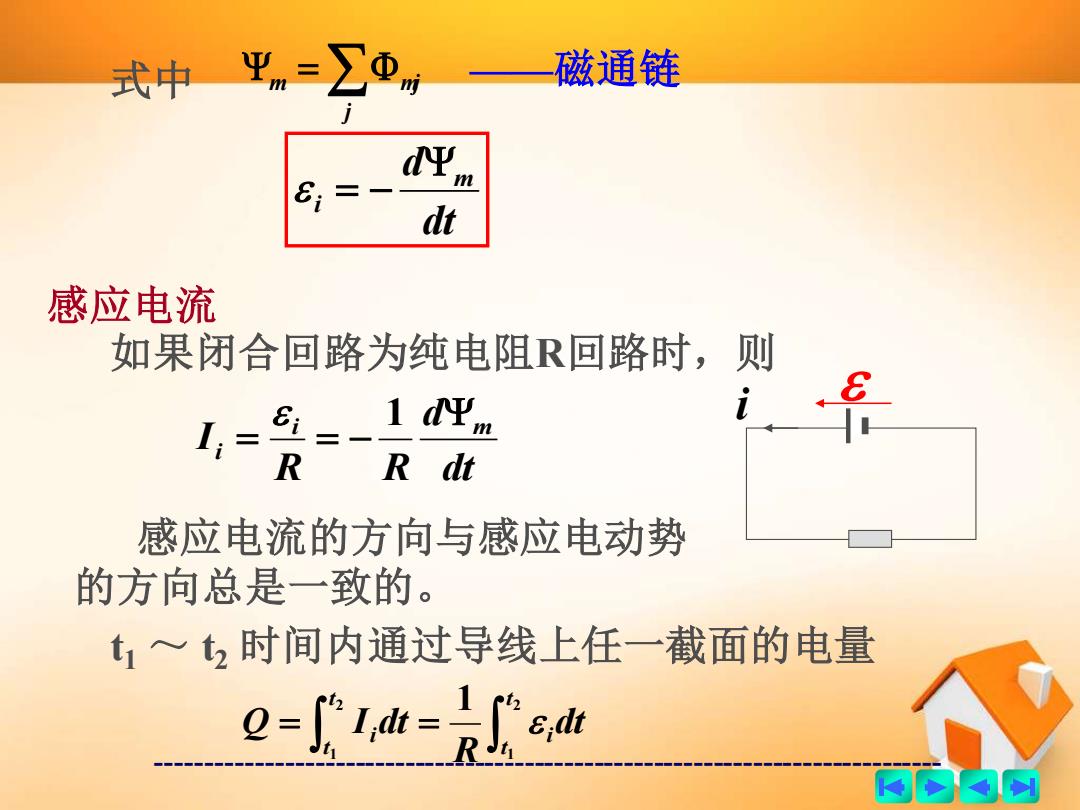
式中平m=∑④ ,一磁通链 61 n dt 感应电流 如果闭合回路为纯电阻R回路时,则 6=- 1 dym R R dt 感应电流的方向与感应电动势 的方向总是一致的。 t1~2时间内通过导线上任一截面的电量 0==cd 西的南的
------------------------------------------------------------------------------- = j 式中 m mj ——磁通链 dt d m i = − 感应电流 如果闭合回路为纯电阻R回路时,则 i dt d R R I i m i = = − 1 感应电流的方向与感应电动势 的方向总是一致的。 t1 ~ t2 时间内通过导线上任一截面的电量 = = 2 1 2 1 1 t t i t t i dt R Q I dt

0=- R ·测Q可以得到△平这就是磁通计的原理。 设回路有N匝线圈 V=NSB 当线圈中磁场由0→B时,不考虑Q的正负,则 0= 1 NSB ∴.B= OR 2NS 阿的内厨
------------------------------------------------------------------------------- dt dt d R Q m m m = − 2 1 1 ( ) 1 m2 m1 R = − − • 测Q 可以得到m这就是磁通计的原理。 设回路有N 匝线圈 m = NSB 当线圈中磁场由0→B时,不考虑Q的正负,则 NSB R Q 1 = NS QR B 2 =

二,楞次定律 1833年,楞次总结出: 闭合回路中感应电流的方向,总是使得它所 激发的磁场来阻止或补偿起感应电流的磁通量 的变化. 产生 磁通量变化 感应电流 阻碍 产生 导线运动 感应电流 阻碍 楞次定律是能量守恒定律在电磁 感应现象上的具体体现 两的肉例
------------------------------------------------------------------------------- 二.楞次定律 1833年,楞次总结出: 闭合回路中感应电流的方向,总是使得它所 激发的磁场来阻止或补偿引起感应电流的磁通量 的变化. 磁通量变化 产生 感应电流 阻碍 a b 导线运动 产生 感应电流 阻碍 f 楞次定律是能量守恒定律在电磁 感应现象上的具体体现

例:一无限长直导线载有交变电流i=insinot,旁边有 一个和它共面的矩形线圈bcd,如图所示求线圈中 的感应电动势. h+12 解:①n=∫B5= h+12 sin wt 2π h 6:= h+2 cos at dt 2π 讨论: 当00,顺时针方向. 的方向还可由楞次定律直接判断。 西的南回
------------------------------------------------------------------------------- 例:一无限长直导线载有交变电流i=i0 sint,旁边有 一个和它共面的矩形线圈abcd,如图所示.求线圈中 的感应电动势. x dx d a b h c l2 l1 i 讨论: 当00,i0,顺时针方向. i的方向还可由楞次定律直接判断. 解: m = B dS + = 2 1 0 2 h l h l dx x i sin t h h l ln i l 0 0 1 2 2 + = dt d m i = − t h i l h l ln cos 0 0 1 2 2 + = −

§9.2动生电动势与感生电动势 感应电动势的非静电力是什么力呢? dΦ dt -5+ dt dt dt 回路变动引起的动生电动势ε 感应电动势 磁场变化引起的→感生电动势ε 一、9 动生电动势 动生电动势的非静电力一洛仑兹力 X X 取导线长dL,导体中载流子速度为u F=Fm=e心×B E=fm=0x B
------------------------------------------------------------------------------- §9.2 动生电动势与感生电动势 感应电动势的非静电力是什么力呢? dt =- dm dt d(B S) = − ( ) dt dS B dt dB S = − + 感应电动势 回路变动引起的→动生电动势ε 磁场变化引起的→感生电动势ε 一、 动生电动势 动生电动势的非静电力——洛仑兹力 Fm 取导线长dl , 导体中载流子速度为u Fk Fm e B = = B e F E m k = =