
材料力学教案第12讲教学方案弯曲内力(1)基本内容弯曲内力、剪力图与弯矩图。1、掌握弯曲变形与平面弯曲等基本概念。教学目2、熟练掌握用截面法求弯曲内力。的熟练列出剪力方程和弯矩方程并绘制剪力图和弯矩图。3、重点本节重点:用截面法求弯曲内力。、难点本节难点:利用剪力方程和弯矩方程绘制剪力图和弯矩图
材 料 力 学 教 案 1 第 12 讲 教学方案 ——弯曲内力(Ⅰ) 基 本 内 容 弯曲内力、剪力图与弯矩图。 教 学 目 的 1、掌握弯曲变形与平面弯曲等基本概念。 2、熟练掌握用截面法求弯曲内力。 3、熟练列出剪力方程和弯矩方程并绘制剪力图和弯矩图。 重 点 、 难 点 本节重点:用截面法求弯曲内力。 本节难点:利用剪力方程和弯矩方程绘制剪力图和弯矩图
进第四章弯曲内力$4-1概述图5-1为工程中常见的桥式起重机大梁和火车轮轴,它们都是受弯构件。弯曲变形:杆件在垂直于其轴线的载荷作用下,使原为直线的轴线变为曲线的变形。通常将承受弯曲变形的杆件称为梁。对称变曲:梁的每一个横截面至少有一根对称轴,这些对称轴构成对称面。所有外力都作用在其对称面内时,梁弯曲变形后的轴线将是位于司作这个对称面内的一条曲线,这种弯曲形式称为对称弯曲,如图5-2所示。对称弯曲是弯曲问题中最常见的情况。(a)P纵向对称面P杆件轴线RR(b)图5-2对称弯曲图5-1受享构件的实例s4-2剪力与弯矩D金(a)静定梁:梁的所有支座反力均可由静力平衡方程确定。静定梁的基本形式有:更童童业业简支梁:一端为固定铰支座,而另一端为可动铰支座的(b)梁,如图5-3a所示。悬臂梁:一端为固定端,另一端为自由端的梁,如图5-3b所示。外伸梁:简支梁的一端或两端伸出支座之外的梁,如图图5-3静定染的基本形式5-3c所示
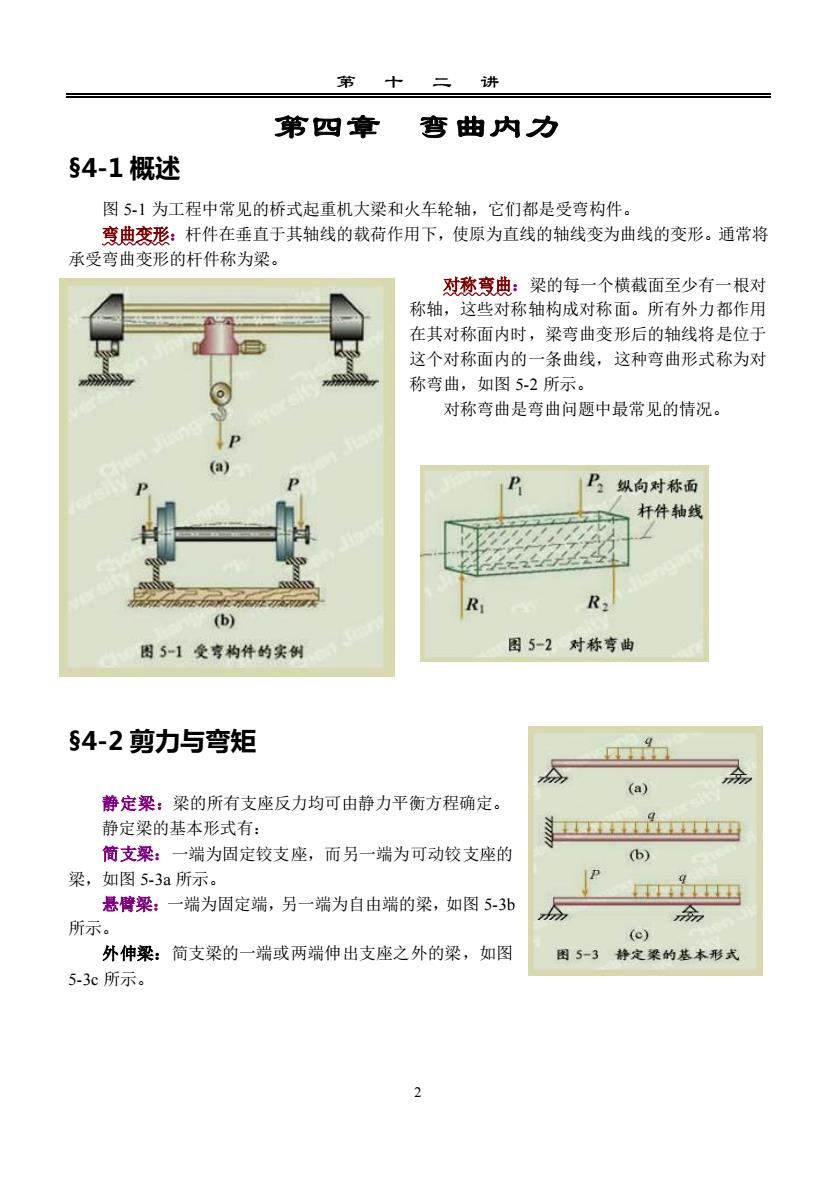
第 十 二 讲 2 第四章 弯曲内力 §4-1 概述 图 5-1 为工程中常见的桥式起重机大梁和火车轮轴,它们都是受弯构件。 弯曲变形:杆件在垂直于其轴线的载荷作用下,使原为直线的轴线变为曲线的变形。通常将 承受弯曲变形的杆件称为梁。 对称弯曲:梁的每一个横截面至少有一根对 称轴,这些对称轴构成对称面。所有外力都作用 在其对称面内时,梁弯曲变形后的轴线将是位于 这个对称面内的一条曲线,这种弯曲形式称为对 称弯曲,如图 5-2 所示。 对称弯曲是弯曲问题中最常见的情况。 §4-2 剪力与弯矩 静定梁:梁的所有支座反力均可由静力平衡方程确定。 静定梁的基本形式有: 简支梁:一端为固定铰支座,而另一端为可动铰支座的 梁,如图 5-3a 所示。 悬臂梁:一端为固定端,另一端为自由端的梁,如图 5-3b 所示。 外伸梁:简支梁的一端或两端伸出支座之外的梁,如图 5-3c 所示
材料力学教察s4-3剪力与弯矩方程剪力图与弯矩图如图 5-4a所示的简支梁,其两端的支座反力R、R,可由梁的静力平衡方程求得。用假想截面将梁分为两部分,并以左段为研究对象(图5-4b)。由于梁的整体处于平衡状态,因此其各个部分也应处于平衡状态。据此,截面I-I上将产生内力,这些内力将与外力P、R,在梁的左段构成平衡力系。apB由平衡方程Y=0,则CT4R,-P-Q=0(a)PRSRAPQ=R,-PD这一与横截面相切的内力O称为横截面miQMO1-1上的剪力,它是与横截面相切的分布内力系的合力。(o)RERA(b)根据平衡条件,若把左段上的所有外图 5-4 用截面法求梁的内力力和内力对截面1-1的形心O取矩,其力矩总和应为零,即m。=0,则M+P(x-a)-R,x=0M=Rx-P(x-a)这一内力偶矩M称为横截面I-1上的弯矩。它是与横截面垂直的分布内力系的合力偶矩。剪力和弯矩均为梁横截面上的内力,它们可以通过梁的局部平衡来确定。剪力、弯矩的正负号规定:使梁产生顺时针转动的剪力规定为正,反之为负,如图5-5所示使梁的下部产生拉伸而上部产生压缩的弯矩规定为正,反之为负,如图5-6所示。000图5-5剪力特号的规定
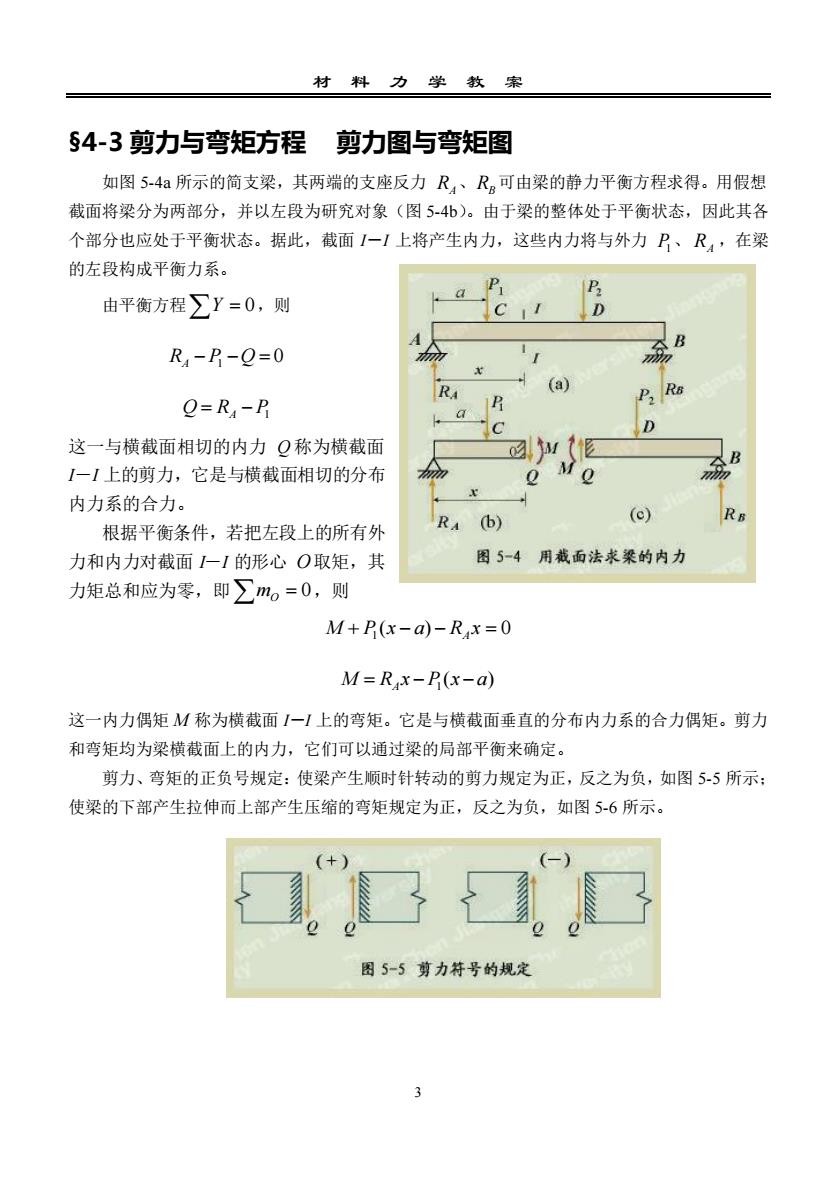
材 料 力 学 教 案 3 §4-3 剪力与弯矩方程 剪力图与弯矩图 如图 5-4a 所示的简支梁,其两端的支座反力 RA、RB 可由梁的静力平衡方程求得。用假想 截面将梁分为两部分,并以左段为研究对象(图 5-4b)。由于梁的整体处于平衡状态,因此其各 个部分也应处于平衡状态。据此,截面 I―I 上将产生内力,这些内力将与外力 P1、 RA ,在梁 的左段构成平衡力系。 由平衡方程 Y = 0 ,则 RA − P1 −Q = 0 Q = RA − P1 这一与横截面相切的内力 Q 称为横截面 I―I 上的剪力,它是与横截面相切的分布 内力系的合力。 根据平衡条件,若把左段上的所有外 力和内力对截面 I―I 的形心 O 取矩,其 力矩总和应为零,即 mO = 0 ,则 M + P1 (x − a) − RA x = 0 ( ) M = RA x − P1 x −a 这一内力偶矩 M 称为横截面 I―I 上的弯矩。它是与横截面垂直的分布内力系的合力偶矩。剪力 和弯矩均为梁横截面上的内力,它们可以通过梁的局部平衡来确定。 剪力、弯矩的正负号规定:使梁产生顺时针转动的剪力规定为正,反之为负,如图 5-5 所示; 使梁的下部产生拉伸而上部产生压缩的弯矩规定为正,反之为负,如图 5-6 所示

讲第O图5-6弯矩符号的规定一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化,将剪力和弯矩沿梁轴线的变化情况用图形表示出来,这种图形分别称为剪力图和弯短图。画剪力图和弯矩图的基本方法有二种:1.剪力、弯矩方程法若以横坐标 x表示横截面在梁轴线上的位置,则各横截面上的剪力和弯矩可以表示为x的函数,即Q=Q(x)M= M(x)上述函数表达式称为梁的剪力方程和弯矩方程。根据剪力方程和弯矩方程即可画出剪力图和弯矩图。画剪力图和弯矩图时,首先要建立Q-x和M-x坐标。一般取梁的左端作为x坐标的原点,Q坐标和M坐标向上为正。然后根据截荷情况分段列出Q(x)和M(a)方程。由截面法和平衡条件可知,在集中力、集中力偶和分布载荷的起止点处,剪力方程和弯矩方程可能发生变化,所以这些点均为剪力方程和弯矩方程的分段点。分段点截面也称控制截面。求出分段点处横截面上剪力和弯矩的数值(包括正负号),并将这些数值标在Q-x、M-x坐标中相应位置处。分段点之间的图形可根据剪力方程和弯矩方程绘出。最后注明l和M的数值。例4-1简支梁受力如图a所示。试写出梁的剪力方程和弯矩方程,并作剪力图和弯矩图。解:(1)求支座反力由平衡方程mg=0和m^=0分别求得R,=ql,R=ql利用平衡方程y=0对所求反力进行校核。(2)建立剪力方程和弯矩方程以梁的左端为坐标原点,建立x坐标,如图a所示。因在C处分布载荷的集度发生变化,故分二段建立剪力方程和弯矩方程。4
第 十 二 讲 4 一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化,将剪力和弯矩沿梁轴线的变 化情况用图形表示出来,这种图形分别称为剪力图和弯矩图。画剪力图和弯矩图的基本方法有二 种: 1.剪力、弯矩方程法 若以横坐标 x 表示横截面在梁轴线上的位置,则各横截面上的剪力和弯矩可以表示为 x 的 函数,即 ( ) ( ) M M x Q Q x = = 上述函数表达式称为梁的剪力方程和弯矩方程。根据剪力方程和弯矩方程即可画出剪力图和弯矩 图。 画剪力图和弯矩图时,首先要建立 Q − x 和 M − x 坐标。一般取梁的左端作为 x 坐标的 原点, Q 坐标和 M 坐标向上为正。然后根据截荷情况分段列出 Q(x) 和 M (x) 方程。由截面 法和平衡条件可知,在集中力、集中力偶和分布载荷的起止点处,剪力方程和弯矩方程可能发生 变化,所以这些点均为剪力方程和弯矩方程的分段点。分段点截面也称控制截面。求出分段点处 横截面上剪力和弯矩的数值(包括正负号),并将这些数值标在 Q − x 、M − x 坐标中相应位置 处。分段点之间的图形可根据剪力方程和弯矩方程绘出。最后注明 max Q 和 M max 的数值。 例 4-1 简支梁受力如图 a 所示。试写出梁的剪力方程和弯矩方程,并作剪力图和弯矩图。 解:(1)求支座反力 由平衡方程 mB = 0 和 mA = 0 分别求得 R ql A 8 3 = , R ql B 8 1 = 利用平衡方程 y = 0 对所求反力进行校核。 (2)建立剪力方程和弯矩方程 以梁的左端为坐标原点,建立 x 坐标,如图 a 所示。 因在 C 处分布载荷的集度发生变化,故分二段建立剪力方程和弯矩方程

AC段:(a)分1-Re--glf音心1289(c)例5-1图(0<x≤Q(n)=ql-qxM,(x) (0≤X≤qxCB 段:Q2(x)=-(≤x<1)o9l(G≤x≤1)M,(x) =ql(1-x)3.求控制截面内力,绘Q、M图Q图:AC段内,剪力方程Q(x)是x的一次函数,剪力图为斜直线,故求出两个端截面的剪力值,Qa右=ql,Qc左=-ql,分别以a、c标在Q-x坐标中,连接a、c的直线即为该段的剪力图。CB段内,剪力方程为常数,求出其中任一截面的内力值,例如Q=-gl,连一水平线即为该段剪力图。梁AB的剪力图如图b所示。M图:AC段内,弯矩方程M,(x)是x的二次函数,表明弯矩图为二次曲线,求出两个端截面ql2,分别以ac标在M-x坐标中。由剪力图知在d点处Q=0,的弯矩,MA=0,Mc=16 将M-gF,以4点标该处弯矩取得极值。令剪力方程Q(x)=0,解得x=在M-x坐标中。据a、d、c三点绘出该段的弯矩图。CB段内,弯矩方程M,(x)是x的一次函数,分别求出两个端点的弯矩,以c、b标在M-x坐标中,并连成直线。AB梁的M图如图c所示
材 料 力 学 教 案 5 AC 段: Q x = ql − qx 8 3 ( ) 1 ) 2 (0 l x 2 1 2 1 8 3 M (x) = qlx − qx ) 2 (0 l x CB 段: Q x ql 8 1 ( ) 2 = − ) 2 ( x l l ( ) 8 1 ( ) 2 M x = ql l − x ) 2 ( x l l 3.求控制截面内力,绘 Q 、 M 图 Q 图:AC 段内,剪力方程 ( ) 1 Q x 是 x 的一次函数,剪力图为斜直线,故求出两个端截面的 剪力值, Q ql A 8 3 右 = ,Q ql C 8 1 左 = − ,分别以 a、c 标在 Q − x 坐标中,连接 a、c 的直线即为 该段的剪力图。CB 段内,剪力方程为常数,求出其中任一截面的内力值,例如 Q ql B 8 1 左 = − , 连一水平线即为该段剪力图。梁 AB 的剪力图如图 b 所示。 M 图:AC 段内,弯矩方程 ( ) 1 M x 是 x 的二次函数,表明弯矩图为二次曲线,求出两个端截面 的弯矩, M A = 0, 2 16 1 M ql C = ,分别以 a、c 标在 M − x 坐标中。由剪力图知在 d 点处 Q = 0 , 该处弯矩取得极值。令剪力方程 Q1 (x) = 0 ,解得 x l 8 3 = ,求得 2 1 128 9 ) 8 3 M ( l = ql ,以 d 点标 在 M − x 坐标中。据 a、d 、c 三点绘出该段的弯矩图。CB 段内,弯矩方程 ( ) 2 M x 是 x 的一次 函数,分别求出两个端点的弯矩,以 c、b 标在 M − x 坐标中,并连成直线。AB 梁的 M 图如图 c 所示