
材料力学教案第2讲教学方案拉压杆的内力和应力基本内容杆件轴向拉伸与压缩时的内力与应力计算1、通过几个杆件拉压的工程实例,建立从工程实例向计算模型简化教学目的初步概念,并给出拉压杆的几个基本概念。2、熟练掌握轴力图的绘制方法。的3、理解掌握横截面与任意斜截面上应力的计算公式和推导方法。重点本节重点:轴力与轴力图,拉压杆的应力计算。,难点本节难点:拉压杆应力计算公式推导过程中的平面假设
材 料 力 学 教 案 1 第 2 讲 教学方案 ——拉压杆的内力和应力 基 本 内 容 杆件轴向拉伸与压缩时的内力与应力计算 教 学 目 的 1、通过几个杆件拉压的工程实例,建立从工程实例向计算模型简化 的初步概念,并给出拉压杆的几个基本概念。 2、熟练掌握轴力图的绘制方法。 3、理解掌握横截面与任意斜截面上应力的计算公式和推导方法。 重 点 、 难 点 本节重点:轴力与轴力图,拉压杆的应力计算。 本节难点:拉压杆应力计算公式推导过程中的平面假设
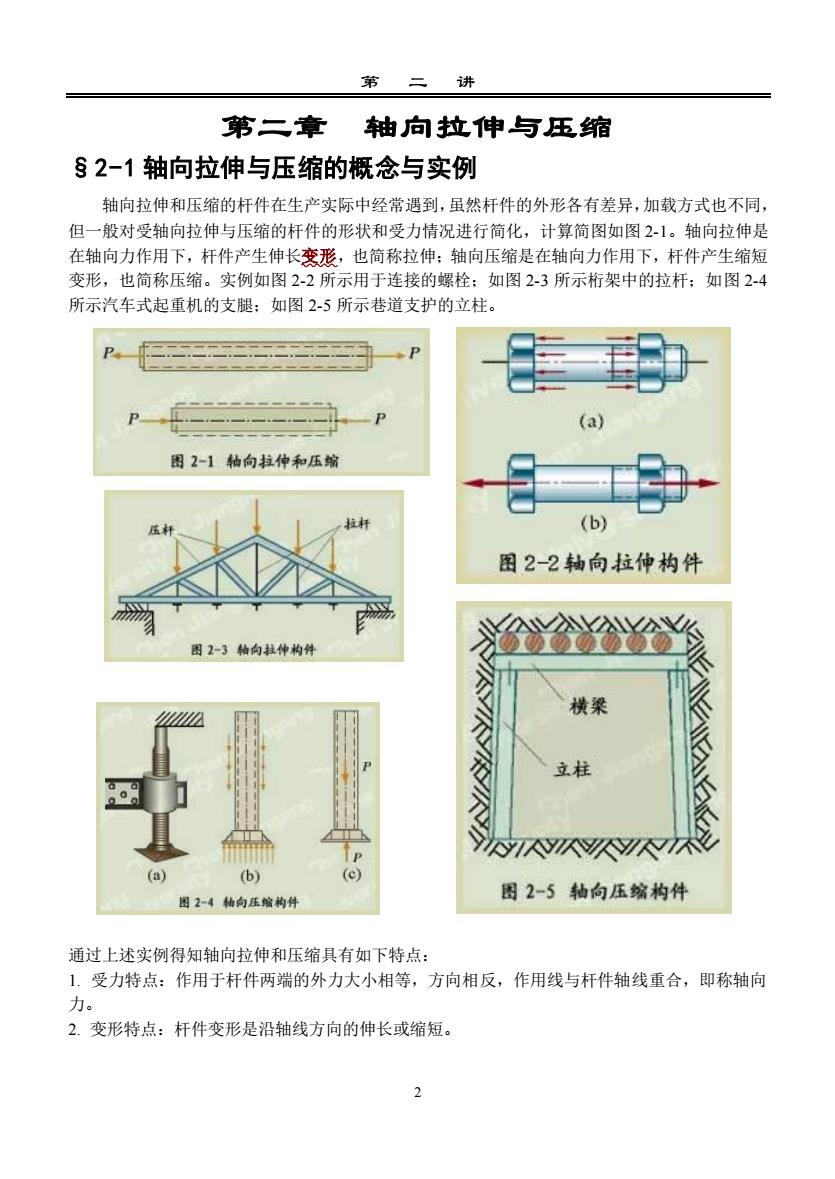
第第二章轴向拉伸与压缩s 2-1 轴向拉伸与压缩的概念与实例轴向拉伸和压缩的杆件在生产实际中经常遇到,虽然杆件的外形各有差异,加载方式也不同,但一般对受轴向拉伸与压缩的杆件的形状和受力情况进行简化,计算简图如图2-1。轴向拉伸是在轴向力作用下,杆件产生伸长变形,也简称拉伸;轴向压缩是在轴向力作用下,杆件产生缩短变形,也简称压缩。实例如图2-2所示用于连接的螺栓:如图2-3所示桁架中的拉杆:如图2-4所示汽车式起重机的支腿;如图2-5所示巷道支护的立柱。P(a)图2-1轴向拉仲和压缩(b)井图2-2轴向拉伸构件图2-3轴向拉仲构件横粱()图2-5轴向压缩构件日2-4轴向压缩构件通过上述实例得知轴向拉伸和压缩具有如下特点:1.受力特点:作用于杆件两端的外力大小相等,方向相反,作用线与杆件轴线重合,即称轴向力。2.变形特点:杆件变形是沿轴线方向的伸长或缩短。2
第 二 讲 2 第二章 轴向拉伸与压缩 §2-1 轴向拉伸与压缩的概念与实例 轴向拉伸和压缩的杆件在生产实际中经常遇到,虽然杆件的外形各有差异,加载方式也不同, 但一般对受轴向拉伸与压缩的杆件的形状和受力情况进行简化,计算简图如图 2-1。轴向拉伸是 在轴向力作用下,杆件产生伸长变形,也简称拉伸;轴向压缩是在轴向力作用下,杆件产生缩短 变形,也简称压缩。实例如图 2-2 所示用于连接的螺栓;如图 2-3 所示桁架中的拉杆;如图 2-4 所示汽车式起重机的支腿;如图 2-5 所示巷道支护的立柱。 通过上述实例得知轴向拉伸和压缩具有如下特点: 1. 受力特点:作用于杆件两端的外力大小相等,方向相反,作用线与杆件轴线重合,即称轴向 力。 2. 变形特点:杆件变形是沿轴线方向的伸长或缩短
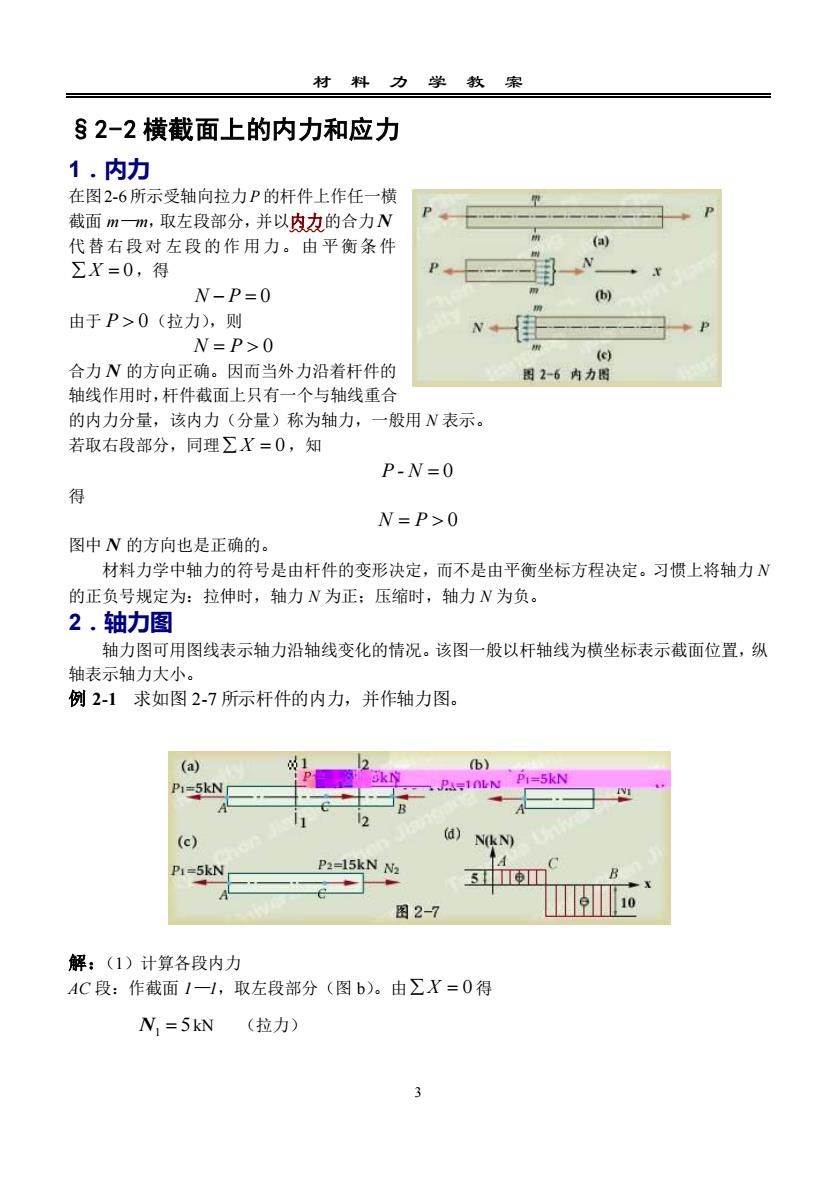
店s2-2横截面上的内力和应力1.内力在图2-6所示受轴向拉力P的杆件上作任一横截面m一m,取左段部分,并以内力的合力N(a)代替右段对左段的作用力。由平衡条件ZX=0,得N-P=0b)由于P>0(拉力)),则N=P>0合力N的方向正确。因而当外力沿着杆件的图2-6内力图轴线作用时,杆件截面上只有一个与轴线重合的内力分量,该内力(分量)称为轴力,一般用N表示。若取右段部分,同理ZX=0,知P-N=0得N=P>0图中N的方向也是正确的。材料力学中轴力的符号是由杆件的变形决定,而不是由平衡坐标方程决定。习惯上将轴力N的正负号规定为:拉伸时,轴力N为正;压缩时,轴力N为负。2.轴力图轴力图可用图线表示轴力沿轴线变化的情况。该图一般以杆轴线为横坐标表示截面位置,纵轴表示轴力大小。例2-1求如图2-7所示杆件的内力,并作轴力图。(a)AJA-10LN PI-5kNPI=5kN(a)N(kN)(c)Pa=-15kN N2Pi=5kN311101110图2-7解:(1)计算各段内力AC段:作截面/—1,取左段部分(图b)。由ZX=0得N,=5kN(拉力)3
材 料 力 学 教 案 3 §2-2 横截面上的内力和应力 1.内力 在图2-6所示受轴向拉力P 的杆件上作任一横 截面 m—m,取左段部分,并以内力的合力 N 代替右段对 左段的作 用力。由 平衡条件 X = 0 ,得 N − P = 0 由于 P 0 (拉力),则 N = P 0 合力 N 的方向正确。因而当外力沿着杆件的 轴线作用时,杆件截面上只有一个与轴线重合 的内力分量,该内力(分量)称为轴力,一般用 N 表示。 若取右段部分,同理 X = 0 ,知 P- N = 0 得 N = P 0 图中 N 的方向也是正确的。 材料力学中轴力的符号是由杆件的变形决定,而不是由平衡坐标方程决定。习惯上将轴力 N 的正负号规定为:拉伸时,轴力 N 为正;压缩时,轴力 N 为负。 2.轴力图 轴力图可用图线表示轴力沿轴线变化的情况。该图一般以杆轴线为横坐标表示截面位置,纵 轴表示轴力大小。 例 2-1 求如图 2-7 所示杆件的内力,并作轴力图。 解:(1)计算各段内力 AC 段:作截面 1—1,取左段部分(图 b)。由 X = 0 得 N1 = 5 kN (拉力)

第讲CB段:作截面2-2,取左缎部分(图),并假设N,方向如图所示。由X=0得N, =-10KN(2)绘轴力图选截面位置为横坐标;相应截面上的轴力为纵坐标,根据适当比例,绘出图线。由图2-7可知CB段的轴力值最大,即M=10kN。注意两个问题:1)求内力时,外力不能沿作用线随意移动(如P2沿轴线移动)。因为材料力学中研究的对象是变形体,不是刚体,力的可传性原理的应用是有条件的。2)截面不能刚好截在外力作用点处(如通过℃点),因为工程实际上并不存在几何意义上的点和线,而实际的力只可能作用于一定微小面积内。例,已知:P=5t,P,=9tND'求:各段内力,并作轴力图解:运用截面法:截、抛、代、平。3VPP-N,=0; P=N,=5t (拉)P-P-N,=0:N,=P-P=-4tAN2)轴力:N为杆件上任一截面上的内力a其作用线垂直于横截面或通过形心即与轴线重合,称之为轴力。3)轴力图:为了把轴力的变化直接显示出来我们平行与杆件轴线引x轴,以横坐标3.轴向拉(压)杆横截面上的应力1)由于只根据轴力并不能判断杆件是否有足够的强度因此必须用横截面上的应力来度量杆件的受力程度。为a了求得应力分布规律,先研究杆件变形,为此提出平面图2-8平面假设假设。平面假设:变形之前横截面为平面,变形之后仍保持为平面,而且仍垂直于杆轴线,如图2-8所示根据平面假设得知,横截面上各点沿轴向的正应变相同,由此可推知横截面上各点正应力也4
第 二 讲 4 CB 段:作截面 2-2,取左缎部分(图),并假设 N2 方向如图所示。由 X = 0 得 N2 = −10KN (2)绘轴力图 选截面位置为横坐标;相应截面上的轴力为纵坐标,根据适当比例,绘出图线。 由图 2-7 可知 CB 段的轴力值最大,即 10 max N = kN。 注意两个问题: 1)求内力时,外力不能沿作用线随意移动(如 P2 沿轴线移动)。因为材料力学中研究的对象是 变形体,不是刚体,力的可传性原理的应用是有条件的。 2)截面不能刚好截在外力作用点处(如通过 C 点),因为工程实际上并不存在几何意义上的点 和线,而实际的力只可能作用于一定微小面积内。 例,已知: P 5t,P 9t 1 = 2 = 求:各段内力,并作轴力图 解:运用截面法:截、抛、代、平。 P1 − N1 = 0 ; P N 5t 1 = 1 = (拉) P1 − P2 − N2 = 0 ; N P P 4t 2 = 1 − 2 = − 2)轴力: N 为杆件上任一截面上的内力 其作用线垂直于横截面或通过形心即与 轴线重合,称之为轴力。 3)轴力图:为了把轴力的变化直接显示出来 我们平行与杆件轴线引 x 轴,以横坐标 3.轴向拉(压)杆横截面上的应力 1)由于只根据轴力并不能判断杆件是否有足够的强度, 因此必须用横截面上的应力来度量杆件的受力程度。为 了求得应力分布规律,先研究杆件变形,为此提出平面 假设。 平面假设:变形之前横截面为平面,变形之后仍保持为平面,而且仍垂直于杆轴线,如图 2-8 所示。 根据平面假设得知,横截面上各点沿轴向的正应变相同,由此可推知横截面上各点正应力也

学教室相同,即α等于常量。2)由静力平衡条件确定α的大小由于dN=α·dA,所以积分得N =[odA= αA则(2-1)g=式中:α一横截面上的正应力PtN一横截面上的轴力图2-9更载面上的应力A一横截面面积正应力的正负号规定为:拉应力为正,压应力为负。对于图2-9所示斜度不大的变截面直杆,在考虑杆自重(容重)引起的正应力时,也可应用(2-1)式0-M(2-2)A.其中N,=P+A,·x若不考虑自重,则N,=P对于等截面直杆,由式(2-1)知最大正应力发生在最图2-10大轴力处,此处最易破坏。而对于变截面直杆,最大正应力的大小不但要考虑N,,同时还要考虑A必须指出,实际构件两端并非直接作用着一对轴向力,而是作用着与两端加载方式有关的分布力,轴向力只是它们静力等效的合力,如图2-2、2-4中的轴向力是通过螺齿作用呈轴对轴分布的分布力的合力。圣维南原理指出:如将作用于构件上某一小区域内的外力系(外力大小不超过一定值)用一静力等效力系来代替,则这种代替对构件内应力与应变的影响只限于离原受力小区域很近的范围内。对于杆件,此范围相当于横向尺寸的1~1.5倍。4.轴向拉(压)杆斜截面上的应力有时拉(压)杆件沿斜截面发生破坏,此时如何确定斜截面k一k上的应力?设等直杆的轴向拉力为P(如图2-12),横截面面积为A,由于k—k截面上的内力仍为P, =P5
材 料 力 学 教 案 5 相同,即 等于常量。 2)由静力平衡条件确定 的大小 由于 dN = dA ,所以积分得 N dA A A = = 则 A N = (2-1) 式中: —横截面上的正应力 N —横截面上的轴力 A —横截面面积 正应力 的正负号规定为:拉应力为正,压应力为负。 对于图 2-9 所示斜度不大的变截面直杆,在考虑杆自重(容重 )引起的正应力时,也可应用(2-1) 式 x x x A N = (2-2) 其中 N P A x x x = + 若不考虑自重,则 Nx = P 对于等截面直杆,由式(2-1)知最大正应力发生在最 大轴力处,此处最易破坏。而对于变截面直杆,最大 正应力的大小不但要考虑 Nx ,同时还要考虑 Ax 。 必须指出,实际构件两端并非直接作用着一对轴向力,而是作用着与两端加载方式有关的 分布力,轴向力只是它们静力等效的合力,如图 2-2、2-4 中的轴向力是通过螺齿作用呈轴对轴 分布的分布力的合力。圣维南原理指出:如将作用于构件上某一小区域内的外力系(外力大小不 超过一定值)用一静力等效力系来代替,则这种代替对构件内应力与应变的影响只限于离原受力 小区域很近的范围内。对于杆件,此范围相当于横向尺寸的 1~1.5 倍。 4.轴向拉(压)杆斜截面上的应力 有时拉(压)杆件沿斜截面发生破坏,此时如何确定斜截面 k—k 上的应力? 设等直杆的轴向拉力为 P (如图 2-12),横截面面积为 A ,由于 k—k 截面上的内力仍为 Pα = P
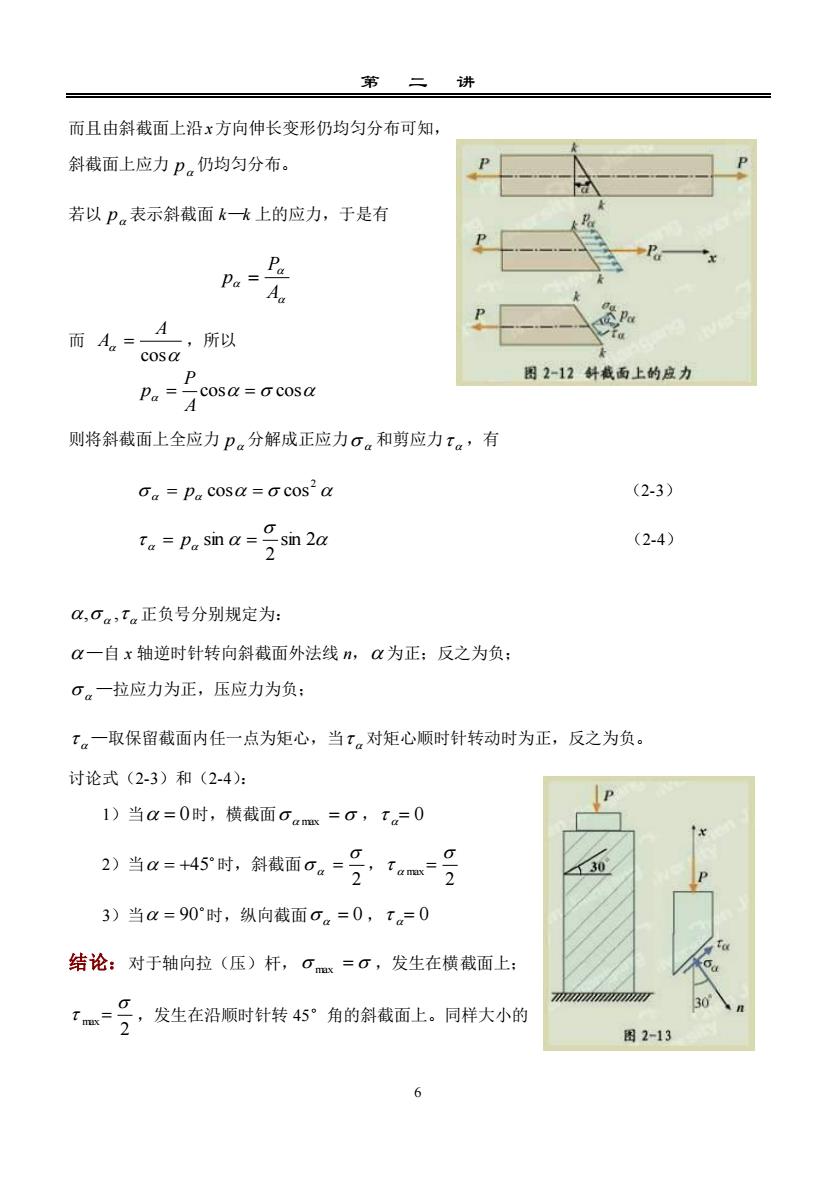
第讲而且由斜截面上沿x方向伸长变形仍均匀分布可知,斜截面上应力p。仍均匀分布。若以p。表示斜截面k—k上的应力,于是有PAu而A所以cosα图2-12斜截面上的应力Pa-cosα=cosα则将斜截面上全应力p。分解成正应力和剪应力t。,有(2-3)α= pa cosα=cosαTa= Pa sin α=sin 2α(2-4)α,α,Ta正负号分别规定为α一自x轴逆时针转向斜截面外法线n,α为正:反之为负:α。一拉应力为正,压应力为负;t。一取保留截面内任一点为矩心,当t。对矩心顺时针转动时为正,反之为负。讨论式(2-3)和(2-4)p1)当α=0时,横截面αamx=G, T=02)当α=+45°时,斜截面。Tame3)当α=90°时,纵向截面。=0,=0结论:对于轴向拉(压)杆,Cmx=α,发生在横截面上;,发生在沿顺时针转45°角的斜截面上。同样大小的mer=图2-136
第 二 讲 6 而且由斜截面上沿x方向伸长变形仍均匀分布可知, 斜截面上应力 p 仍均匀分布。 若以 p 表示斜截面 k—k 上的应力,于是有 A P p = 而 cos A A = ,所以 = cos = cos A P p 则将斜截面上全应力 p 分解成正应力 和剪应力 ,有 2 = p cos = cos (2-3) sin 2 2 = p sin = (2-4) , , 正负号分别规定为: —自 x 轴逆时针转向斜截面外法线 n, 为正;反之为负; —拉应力为正,压应力为负; —取保留截面内任一点为矩心,当 对矩心顺时针转动时为正,反之为负。 讨论式(2-3)和(2-4): 1)当 = 0 时,横截面 max = , = 0 2)当 = +45 时,斜截面 2 = , 2 max = 3)当 = 90 时,纵向截面 = 0 , = 0 结论:对于轴向拉(压)杆, max = ,发生在横截面上; 2 max = ,发生在沿顺时针转 45°角的斜截面上。同样大小的

材料力学教剪应力也发生在α=-45°的斜面上。例24木立柱承受压力P,上面放有钢块。如图2-13所示,钢块截面积A,为2×2cm20锅=35MPa,木柱截面积A,=8×8cm2,求木柱顺纹方向剪应力大小及指向。解:(1)计算木柱压力P,由PCm=A所以P=m=A,=35×10°×2×2×10=14kN(压力)(2)计算木柱的剪应力t30横截面上P14×103×10-6 = 2.19MPa a:(压应力)A,64×10-则sin(2×30°)=0.95MPaT30=30指向如图所示
材 料 力 学 教 案 7 剪应力也发生在 = −45 的斜面上。 例 2-4 木立柱承受压力 P ,上面放有钢块。如图 2-13 所示,钢块截面积 A1 为 2 2 cm2, 钢 = 35 MPa,木柱截面积 A2 = 88 cm2,求木柱顺纹方向剪应力大小及指向。 解:(1)计算木柱压力 P ,由 A1 P 钢 = 所以 35 10 2 2 10 14 6 4 = = = − P 钢 A1 kN(压力) (2)计算木柱的剪应力 30 横截面上 10 2 19 64 10 14 10 6 4 3 . A P 2 = = = − − MPa (压应力) 则 2 30 0 95 2 0 30 = sin( ) = . MPa 30 指向如图所示