
质点及质点组力学 复习和习题课
质点及质点组力学 复习和习题课

前两章概念回顾 ·质点运动描述:位移,速度,加速度,轨道 ·牛顿三定律,质点(系)动量定理及守恒律 ·质点(系)角动量定理及守恒律 ·质点(系)动能定理及机械能守恒律 ·保守力与势能曲线 ·两体问题,质心系和实验室系
前两章概念回顾 • 质点运动描述: 位移, 速度, 加速度, 轨道 • 牛顿三定律, 质点(系)动量定理及守恒律 • 质点(系)角动量定理及守恒律 • 质点(系)动能定理及机械能守恒律 • 保守力与势能曲线 • 两体问题, 质心系和实验室系

例1(质点运动学)由光滑钢丝弯成竖直平面里的一条曲线,质点 穿在此钢丝上,可沿着它滑动(图).已知其切向加速度为-g$in8,日 是曲线切向与水平方向的夹角.试求质点在各处的速度: 解:取直角坐标系如图.令ds为 质点移动的弧长,在y方向上投影 为dy=ds sin6.这里只用到切向加 速度 =-8sn0 dt 由此 积分 「dv=-8dy,→v2-=2g0,-y
例1 (质点运动学) 由光滑钢丝弯成竖直平面里的一条曲线, 质点 穿在此钢丝上,可沿着它滑动(图). 已知其切向加速度为-gsin, 是曲线切向与水平方向的夹角. 试求质点在各处的速度. 解: 取直角坐标系如图. 令ds 为 质点移动的弧长, 在y方向上投影 为dy =ds sin. 这里只用到切向加 速度 sin d d g t v at = = − 由此 O g dy ds x y g y v t s t g y s y v g t g d / d d d d d d d sin d 1 = − = − = − = − − 积分 d d , 2 ( ) 0 2 0 2 0 0 v v g y v v g y y y y v v = − − = −

例2(质点运动方程)小雨点与大雨点相比,在空中哪个降落的比 较快?空气阻力为f阻CS2.S为雨点表面积,为雨点速度,C是 常 解:当雨点在云层形成以后,即在重力作用下加速降落.随着雨点 速度的加大,空气阻力由0加大到与雨点的重力g抗衡: CSv2 mg 此后它将不再受力,以一定的速度作匀速直线运动.雨点最后的 速度叫终极速度.令 S=m2,m=4πpwae 3 终极速度为 Vterminal 4 rgpwater 1 3C 故大雨点比小雨点下落的快!
例2 (质点运动方程) 小雨点与大雨点相比, 在空中哪个降落的比 较快? 空气阻力为f阻=CSv2 . S为雨点表面积, v为雨点速度, C是 常数. 解: 当雨点在云层形成以后, 即在重力作用下加速降落. 随着雨点 速度的加大, 空气阻力由 0 加大到与雨点的重力mg抗衡: CSv = mg 2 此后它将不再受力, 以一定的速度作匀速直线运动. 雨点最后的 速度叫终极速度. 令 , 4 / 3 2 3 water S = r m = r 终极速度为 r C rg v water = 3 4 terminal 故大雨点比小雨点下落的快!
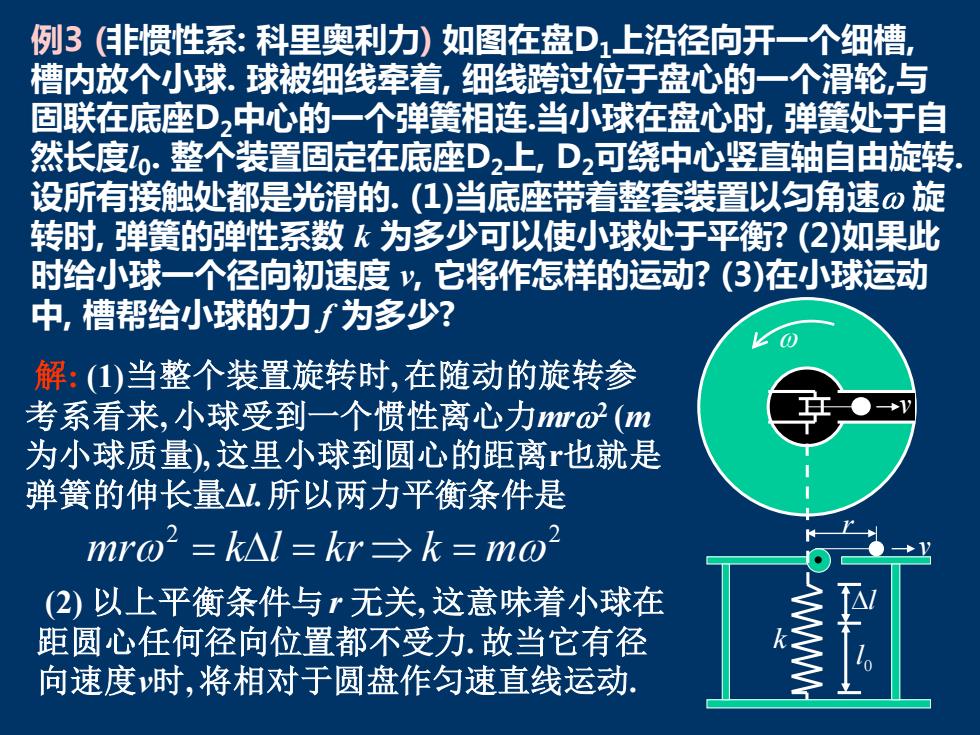
例3(非惯性系:科里奥利力)如图在盘D上沿径向开一个细槽, 槽内放个小球.球被细线牵着,细线跨过位于盘心的一个滑轮,与 固联在底座D,中心的一个弹簧相连.当小球在盘心时,弹簧处于自 然长度,.整个装置固定在底座D2上,D,可绕中心竖直轴自由旋转 设所有接触处都是光滑的.(1)当底座带着整套装置以匀角速ω旋 转时,弹簧的弹性系数k为多少可以使小球处于平衡?(2)如果此 时给小球一个径向初速度y,它将作怎样的运动?(3)在小球运动 中,槽帮给小球的力f为多少? 解:(1)当整个装置旋转时,在随动的旋转参 考系看来,小球受到一个惯性离心力ro2(m 为小球质量),这里小球到圆心的距离也就是 弹簧的伸长量△.所以两力平衡条件是 mro2=k△l=kr三k=mo2 (2)以上平衡条件与r无关,这意味着小球在 距圆心任何径向位置都不受力.故当它有径 向速度时,将相对于圆盘作匀速直线运动
例3 (非惯性系: 科里奥利力) 如图在盘D1上沿径向开一个细槽, 槽内放个小球. 球被细线牵着, 细线跨过位于盘心的一个滑轮,与 固联在底座D2中心的一个弹簧相连.当小球在盘心时, 弹簧处于自 然长度l0 . 整个装置固定在底座D2上, D2可绕中心竖直轴自由旋转. 设所有接触处都是光滑的. (1)当底座带着整套装置以匀角速 旋 转时, 弹簧的弹性系数 k 为多少可以使小球处于平衡? (2)如果此 时给小球一个径向初速度 v, 它将作怎样的运动? (3)在小球运动 中, 槽帮给小球的力 f 为多少? 解: (1)当整个装置旋转时, 在随动的旋转参 考系看来, 小球受到一个惯性离心力mr2 (m 为小球质量), 这里小球到圆心的距离r也就是 弹簧的伸长量l. 所以两力平衡条件是 2 2 mr = kl = k r k = m (2) 以上平衡条件与r 无关, 这意味着小球在 距圆心任何径向位置都不受力. 故当它有径 向速度v时, 将相对于圆盘作匀速直线运动. k l 0 l r v v

(③)槽帮对小球的力属于束缚力,只能从小球在静止参考系(惯性系) 中的加速度安过来求得.设t=0时刻小球在圆盘上的位置为A,△1时 间后到达B,A'B=v△t(图).在静止系看来,小球最初具有两个速度 分量:径向分量y=和角向分量y。=ro.△t时间后圆盘转过角度 △o△i,y。分量使小球走到4如果没有加速度,此速度分量与y,分 量合成,把小球带到B?点.然而质点实际上到达了B点.位移B'B是 由加速度引起的.利用 BB=a(△r)2 在静止系观察⑦ 另一方面,由图可以看出 AB=v1,B'B=AB·△p=vo(△t) 所以 a=2vo 这加速度是槽帮给小球的约束力造成的.所以 f ma=2mvo
(3)槽帮对小球的力属于束缚力,只能从小球在静止参考系(惯性系) 中的加速度安过来求得. 设 t =0时刻小球在圆盘上的位置为A, t 时 间后到达B, A’B=v t (图). 在静止系看来, 小球最初具有两个速度 分量: 径向分量 vr =v和角向分量v =r. t 时间后圆盘转过角度 =t, v分量使小球走到A’.如果没有加速度, 此速度分量与vr分 量合成, 把小球带到B’点. 然而质点实际上到达了B点. 位移B’B是 由加速度引起的. 利用 在静止系观察 O A A’ B B’ 2 2 1 B'B = a(t) 另一方面,由图可以看出 ( ) 2 A'B = vt,B'B = A'B = v t 所以 a = 2v 这加速度是槽帮给小球的约束力造成的. 所以 f = ma = 2mv

例4(质点组运动方程)一质量为m,长为的完全柔软绳 子竖直地悬挂着,其下端刚刚与地面接触.放开它,使之 自静止下落.求下落到所剩长度为时地面对这段绳子 的作用力设绳子质量均匀. 解:自始至终把整个绳子当作质点组, 计算它的质心高度 Vc= dt l dt 式中dz/dv是绳子上端的下落速度, 对于完全柔软的绳子,它和一个自由 质点的下落速度相同
例4 (质点组运动方程) 一质量为m, 长为l的完全柔软绳 子竖直地悬挂着, 其下端刚刚与地面接触. 放开它,使之 自静止下落. 求下落到所剩长度为z时地面对这段绳子 的作用力.设绳子质量均匀. l l-z z f m 解: 自始至终把整个绳子当作质点组, 计算它的质心高度 , 2 d 1 2 0 l z z z l m m z z C = = , d d d d t z l z t z v C C = = 式中dz/dt=v是绳子上端的下落速度. 对于完全柔软的绳子, 它和一个自由 质点的下落速度相同

v=-v2g(I-z) 质心加速度为 di 式中dv/d仁-g是绳子下落的加速度,所以 ac=2g(1-)-音g 对整根绳子应用质心运动定理 f-mg=mac .f=3mg1-)
v = − 2g(l − z) 质心加速度为 t v l z l v v l z t t v a C C d d d d d d 2 = + = = 式中dv/dt=-g是绳子下落的加速度, 所以 a g gl z l z C = 2 (1− ) − 对整根绳子应用质心运动定理 mg maC f − = ( )l mg z f = 3 1−

例5(机械能)火箭从地球表面发射需要多大速度才能脱 离太阳?(第三宇宙速度), 解:这一问题可以分几步计算.从地球公转轨道逃逸, 脱离太阳系,则要求机械能大于等于零 物i GM物≥0 了地对日 得到 2GM角 =42.1×103m/s T地对日 地球绕太阳公转的速度利用向心力和引力相等可以算出
例5 (机械能) 火箭从地球表面发射需要多大速度才能脱 离太阳? (第三宇宙速度). 解: 这一问题可以分几步计算. 从地球公转轨道逃逸, 脱离太阳系, 则要求机械能大于等于零 0 2 1 2 − 地对日 日 物 物 r GM m m v 得到 42.1 10 m/s 2 3 = 地对日 日 r GM v 地球绕太阳公转的速度利用向心力和引力相等可以算出

V地公转 =30×103m/s 地对日 所以从地球发射物体时,可以选择发射方向和公转方向 一致,那么只要相对地球以12.1 103m/s,相对于太阳 就能达到42.1 103m/s. 不过物体是在地球表面发射的,所以还要克服地球的 引力.因此第三宇宙速度应近似按下式计算 GMem物=】 m物(12.1×103)2 2 n物V3 地
30 10 m/s 3 = = 地对日 日 地公转 r GM v 所以从地球发射物体时,可以选择发射方向和公转方向 一致, 那么只要相对地球以12.1 103m/s, 相对于太阳 就能达到42.1 103m/s. 不过物体是在地球表面发射的,所以还要克服地球的 引力. 因此第三宇宙速度应近似按下式计算 2 3 2 3 (12.1 10 ) 2 1 2 1 − = 物 地 地 物 物 m r GM m m v