
能量法1功能原理法
能量法1 功能原理法

概述 (Introduction) 一、能量方法(Energy methods) 利用功能原理',=W来求解可变形固体的位移,变形和内力 等的方法。 二、外力功(Work of the external force) 固体在外力作用下变形,引起力作用点沿力作用方向位移, 外力因此而做功,则成为外力功: 三、变形能(Strain energy) 在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄 的能量,称为弹性变形能,简称变形能
概述(Introduction) 在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄 的能量,称为弹性变形能,简称变形能. 一、能量方法 (Energy methods ) 三、变形能(Strain energy) 二、外力功(Work of the external force) 固体在外力作用下变形,引起力作用点沿力作用方向位移, 外力因此而做功,则成为外力功. 利用功能原理 Vε = W 来求解可变形固体的位移,变形和内力 等的方法

四、功能原理 外力由零开始缓慢地增加到最终值,变形中的每一瞬 间固体都处于平衡状态,动能和其他能量的变化皆可不 计,则固体的应变能在数值上等于外力所作的功。 V.-W 外力功的统一表达式 p=)F6 F:广义力,8:广义变形
外力由零开始缓慢地增加到最终值,变形中的每一瞬 间固体都处于平衡状态,动能和其他能量的变化皆可不 计,则固体的应变能在数值上等于外力所作的功。 四、功能原理 V = W 外力功的统一表达式 W F 2 1 = F:广义力, :广义变形
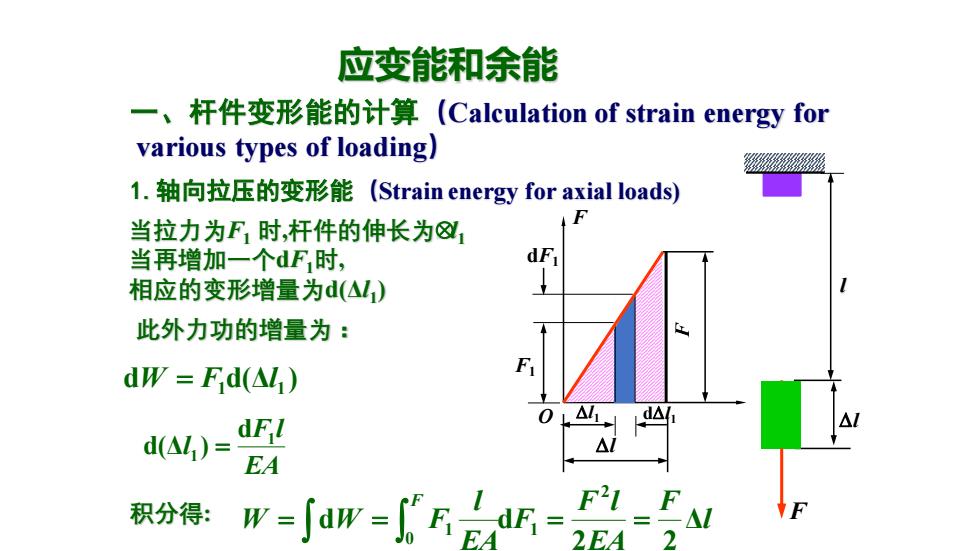
应变能和余能 一、杆件变形能的计算(Calculation of strain energy for various types of loading) 1.轴向拉压的变形能(Strain energy for axial loads) 当拉力为F时,杆件的伸长为⑧ 当再增加一个dF时, dF 相应的变形增量为d(△l) 此外力功的增量为: dw=Fd△M) F dFl d△ d(△)= EA 积分得: w=∫aw=FdE= F21 EA
应变能和余能 一、杆件变形能的计算(Calculation of strain energy for various types of loading) 1.轴向拉压的变形能(Strain energy for axial loads) 此外力功的增量为: d d(Δ ) 1 1 W = F l EA F l l 1 1 d d(Δ ) = 当拉力为F1 时,杆件的伸长为l1 当再增加一个dF1时, 相应的变形增量为d(Δl1 ) F F l l F O l l1 dl1 dF1 F1 积分得: l F EA F l F EA l W W F F Δ 2 2 d d 2 1 0 = = 1 = =

根据功能原理 V=W,可得以下变形能表达式 V.-W-1FM-IFAI 2 2 FI Fl △M= EA EA V.= F21 RI 2EA 2EA 当轴力或截面发生变化时:
V W F l F Δl 2 1 Δ 2 1 ε = = = N EA F l EA Fl l N Δ = = 根据功能原理 当轴力或截面发生变化时: Vε= W , 可得以下变形能表达式 EA F l EA F l V 2 2 2 N 2 ε = = = = n i i i i i E A F l V 1 2 N ε 2

当轴力或截面连续变化时:V。=)心 比能(strain energy density): 单位体积的应变能.记作) 1 U )= Al 2 o=E8 1 σ2_Ee2 V:= -08= (单位J/m3) 2E2
= l EA x F x x V 0 2 N ε 2 ( ) ( )d σε Al F l V U 2 1 Δ 2 1 ε = = = (单位 J/m3 ) 比能 ( strain energy density): 单位体积的应变能. 记作 当轴力或截面连续变化时: σ = Eε 2 2 2 1 2 2 ε Eε E σ = σε = =
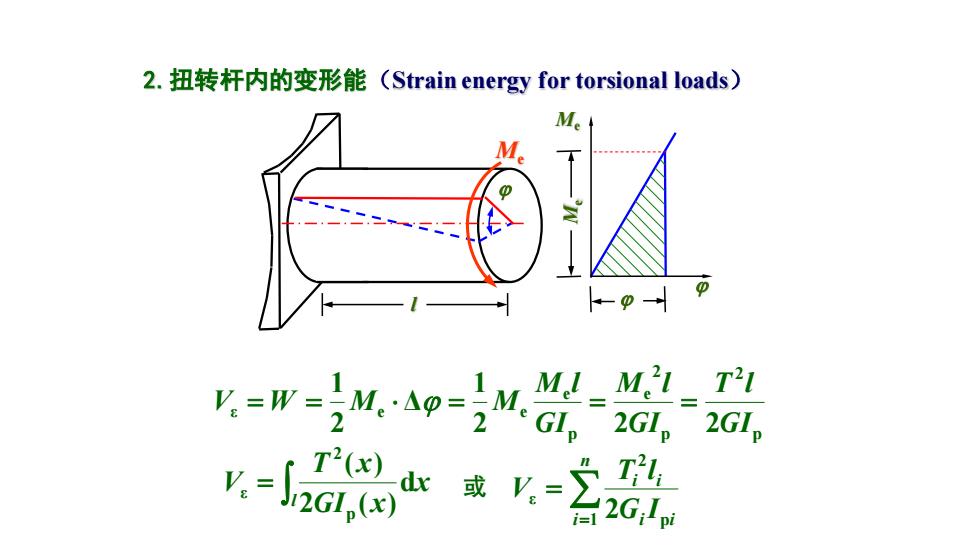
2.扭转杆内的变形能(Strain energy for torsional loads) M M Ml_M.21_ T21 7=W=MA9=2M:G2GL于 2GIp .-18 0“-含
2.扭转杆内的变形能(Strain energy for torsional loads) 或 l p 2 p 2 e p e ε e e 2 2 2 1 Δ 2 1 GI T l GI M l GI M l V = W = M = M = = = l x GI x T x V d 2 ( ) ( ) p 2 ε = = n i i i i i G I T l V 1 p 2 ε 2 Me Me Me

3.弯曲变形的变形能 (Strain energy for flexural loads) ·纯弯曲(pure bending) -08 长=w=M0= MI M'I 2 2E1 ·横力弯曲(nonuniform bending) -
• 纯弯曲(pure bending ) • 横力弯曲(nonuniform bending ) 3.弯曲变形的变形能 (Strain energy for flexural loads) θ Me EI M l EI M l V W M θ M 2 2 1 2 1 2 = = = = e ε e e x EI x M x V l d 2 ( ) ( ) 2 e ε = Me Me Me

4.组合变形的变形能(Strain energy for combined loads) 截面上存在几种内力,各个内力及相应的各个位移相互独立, 力独立作用原理成立,各个内力只对其相应的位移做功: -++ 5.纯剪切应力状态下的比能 (Strain energy density for pure shearing state of stresses) 假设单元体左侧固定,因此变形后右侧将向下移动yx
4.组合变形的变形能(Strain energy for combined loads) 截面上存在几种内力,各个内力及相应的各个位移相互独立, 力独立作用原理成立,各个内力只对其相应的位移做功. x EI x M x x GI x T x x EA x F x V l l l d 2 ( ) ( ) d 2 ( ) ( ) d 2 ( ) ( ) 2 p 2 2 N ε = + + 5.纯剪切应力状态下的比能 (Strain energy density for pure shearing state of stresses) 假设单元体左侧固定,因此变形后右侧将向下移动 dx
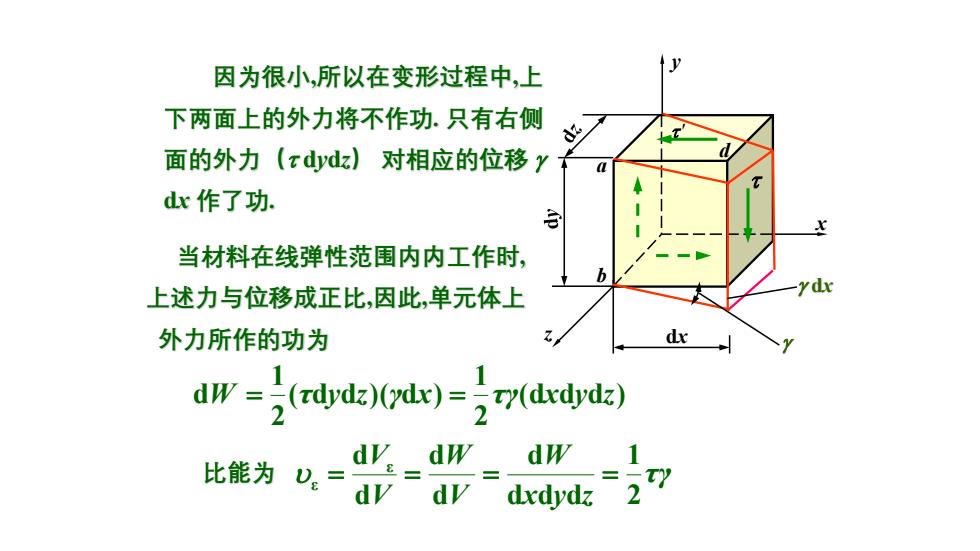
因为很小,所以在变形过程中,上 下两面上的外力将不作功.只有右侧 面的外力(xd山vdz)对相应的位移y dx作了功. 当材料在线弹性范围内内工作时, 上述力与位移成正比,因此,单元体上 外力所作的功为 dx d-(rdpdz)Gd)-r7(ddrdz) dy dw dw 比能为v。= dy dy dxdydz 27
dx x y z a b d 因为很小,所以在变形过程中,上 下两面上的外力将不作功. 只有右侧 面的外力( dydz) 对相应的位移 dx 作了功. dx 当材料在线弹性范围内内工作时, 上述力与位移成正比,因此,单元体上 外力所作的功为 (d d d ) 2 1 ( d d )( d ) 2 1 dW = τ y z γ x = τγ x y z 比能为 τγ x y z W V W V V 2 1 d d d d d d d d ε ε = = = =