
第五章 分析力学
第五章 分析力学

§5.3拉格朗日方程 导读 •达朗贝尔原理 ·基本拉格朗日方程 ·广义速度广义动量 ·保守系的拉格朗日方程 ·循环积分
• 达朗贝尔原理 • 基本拉格朗日方程 • 保守系的拉格朗日方程 导读 §5.3 拉格朗日方程 • 循环积分 • 广义速度 广义动量

1达朗贝尔原理 按照牛顿运动定律,力学系统的第质点的运动方程是 F,+R-m,元=0 只要把最后一项理解为一种力,上式就变为平衡方程的 类型.事实上,研究第质点的运动时,若选用跟随这质点 一同平动的参考系统,这质点显然是(相对)静止的,它应 当遵守平衡方程.最后一项就是惯性力.这就叫作达朗贝 尔原理 ∑(厅-m)苏=0 (5.23) 达朗贝尔拉格朗日方程
按照牛顿运动定律, 力学系统的第i质点的运动方程是 + − = 0 i i i i F R m r 只要把最后一项理解为一种力, 上式就变为平衡方程的 类型. 事实上, 研究第i质点的运动时, 若选用跟随这质点 一同平动的参考系统, 这质点显然是(相对)静止的, 它应 当遵守平衡方程. 最后一项就是惯性力. 这就叫作达朗贝 尔原理. ( ) 0 (5.23) 1 − = = n i i i i i F m r r ——达朗贝尔-拉格朗日方程 1 达朗贝尔原理

达朗贝尔原理是以牛顿定律加上理想约束假定 作为逻辑推理的出发点导出的.从这个基本法出发 再利用约束对虚位移的限制关系式,可以导出力学 系统的动力学方程,从而概括了力学系统的运动规 律.由于约束的性质是纯几何的或运动学的,因此可 认为真正作为动力学理论的逻辑出发点就是这个基 本方程,故称之为“原理”.这比承认牛顿定律再加 上理想约束假定作为出发点更为简洁和富有概括性, 当存在非理想约束时,达朗贝尔原理也适用,它可叙 述为:主动力和非理想约束力及惯性力的虚功之和 为零.对于完整约束或非完整约束,这个原理都适用, 因此它可以称为分析动力学的普遍原理
达朗贝尔原理是以牛顿定律加上理想约束假定 作为逻辑推理的出发点导出的. 从这个基本法出发 再利用约束对虚位移的限制关系式, 可以导出力学 系统的动力学方程,从而概括了力学系统的运动规 律. 由于约束的性质是纯几何的或运动学的, 因此可 认为真正作为动力学理论的逻辑出发点就是这个基 本方程, 故称之为“原理”. 这比承认牛顿定律再加 上理想约束假定作为出发点更为简洁和富有概括性. 当存在非理想约束时, 达朗贝尔原理也适用,它可叙 述为:主动力和非理想约束力及惯性力的虚功之和 为零. 对于完整约束或非完整约束, 这个原理都适用, 因此它可以称为分析动力学的普遍原理

2动力学普遍方程 ∑(f-m,a)6n=0 (i=1,2,m F=匠,FwF小=(民5=6分%6) 方程的直角坐标形式 ∑(-m)6x+(-m,)6+(f。-m)6=0 i=1,2,m 适用于具有理想约束或双面约束的系统: 适用于具有稳定(或非稳定)约束的系统; 适用于具有完整(或非完整)约束的系统; 适用于具有保守力(或非保守力)的系统
i n F m x x F m y y F m z z i i y i i i i z i i i i i x i i = , , , − + − + − = 1 2 ( ) δ ( ) δ ( ) δ 0 方程的直角坐标形式 ( m ) δ 0 (i 1 2 n) i i i i i F − a r = = , , , 适用于具有稳定(或非稳定)约束的系统; 适用于具有完整(或非完整)约束的系统; 适用于具有保守力(或非保守力)的系统。 适用于具有理想约束或双面约束的系统; 2 动力学普遍方程 ( ) ( ) ( ) i i x i y i z i i i i i i i i F = F , F , F , a = x , y , z ,δ r = δ x ,δ y ,δ z

大达朗贝尔一拉格朗日方程主要应用于求解动力 学第二类问题,即:己知主动力求系统的运动规 律。 *应用达朗贝尔一拉格朗日方程求解系统运动 规律时,重要的是正确分析运动,并在系统上施 加惯性力。 应用达朗贝尔一拉格朗日方程时,需要正确 分析主动力和惯性力作用点的虚位移,并正确计 算相应的虚功。 由于达朗贝尔一拉格朗日方程中不包含约束 力,因此,不需要解除约束,也不需要将系统拆 开
* 达朗贝尔-拉格朗日方程主要应用于求解动力 学第二类问题,即:已知主动力求系统的运动规 律。 * 应用达朗贝尔-拉格朗日方程求解系统运动 规律时,重要的是正确分析运动,并在系统上施 加惯性力。 * 由于达朗贝尔-拉格朗日方程中不包含约束 力,因此,不需要解除约束,也不需要将系统拆 开。 * 应用达朗贝尔-拉格朗日方程时,需要正确 分析主动力和惯性力作用点的虚位移,并正确计 算相应的虚功
3应用举例 例题1 离心调速器 已知: m,一球A、B的质量; m2-重锤C的质量; 一杆件的长度; 0一O1y,轴的旋转角速度。 求: o一a的关系
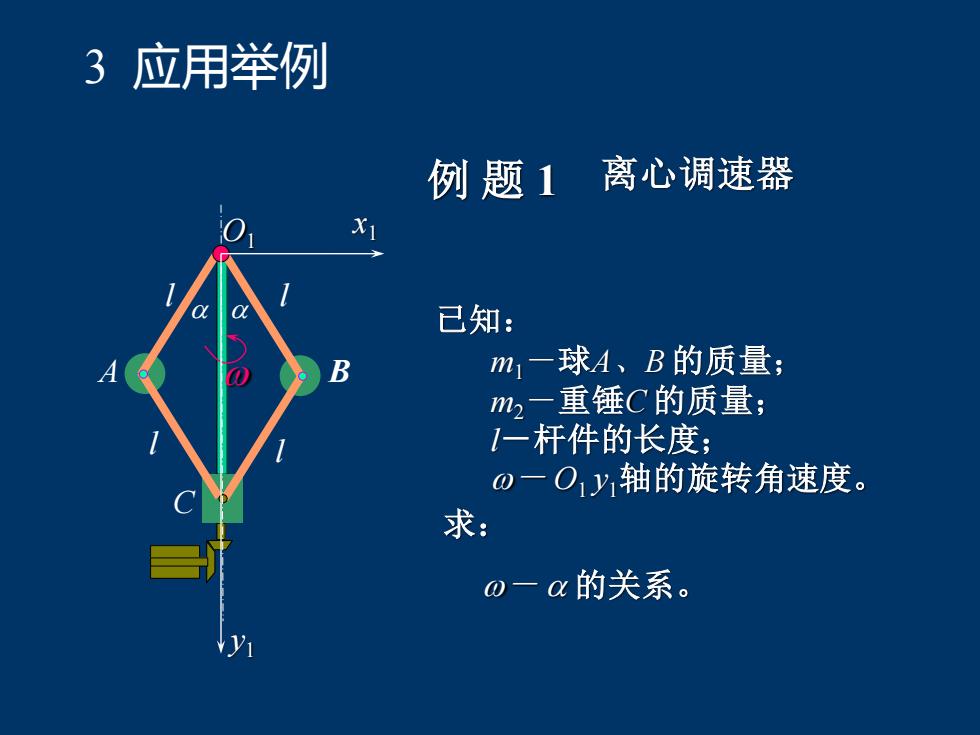
例 题 1 离心调速器 已知: m1-球A、B 的质量; m2-重锤C 的质量; l-杆件的长度; - O1 y1轴的旋转角速度。 求: - 的关系。 A B C l l l l O1 x1 y1 3 应用举例
解:不考虑摩擦力,这一系统的约束为理想约束;系 统具有一个自由度。 取广义坐标q=a 1、分析运动、确定惯性力 球4、B绕轴等速转动;重锤静止不动。 Sa 球A、B的惯性力为Fi4=FB=mlsina B →FB2、给系统有一虚位移。A、B、C 18 718 三处的虚位移分别为δr4、δrB、δrC 3、应用达朗贝尔一拉格朗日方程 28 Fu5 xa+FB8 xB+mg8y +mng6 y8+m2g 8ye=0
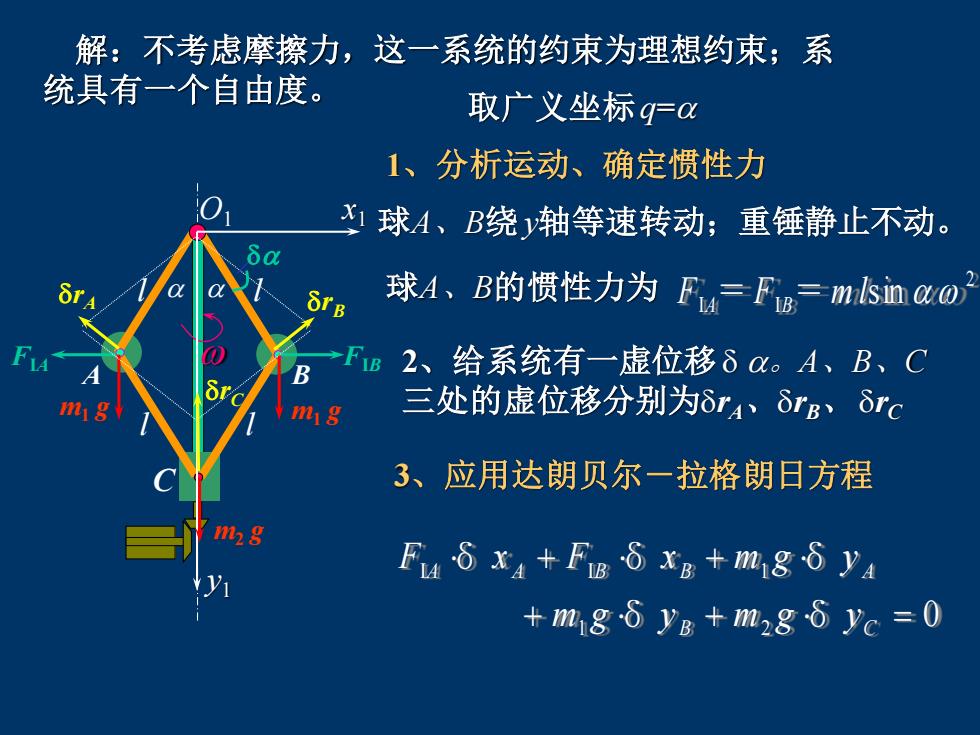
解:不考虑摩擦力,这一系统的约束为理想约束;系 统具有一个自由度。 取广义坐标q= 1、分析运动、确定惯性力 球A、B绕 y轴等速转动;重锤静止不动。 球A、B的惯性力为 2 I I F A = F B = m lsin 2、给系统有一虚位移 。A、B、C 三处的虚位移分别为rA、rB、 rC C l l l l O1 x1 y1 A B FIA FIB m1 g m1 g m2 g rB rA rC 3、应用达朗贝尔-拉格朗日方程 δ δ 0 δ δ δ 1 2 I I 1 + + = + + B C A A B B A m g y m g y F x F x m g y
根据几何关系,有 X=-lsina δx=-lc0saδa B ylcosa oy4=-lsinaòa xs=lsina δxB=lcosaδa Y8=lcosa dyg=-lsinaδa g Yc=2lcosa oyc=-2 lsinaòa F464卡F房6卡m86y4+86yg+m28ye=0 2milsimaolcosas a-2mglsin a8 a-2m2glsim a8 a=0 o2=m1+m,8 m lcosa
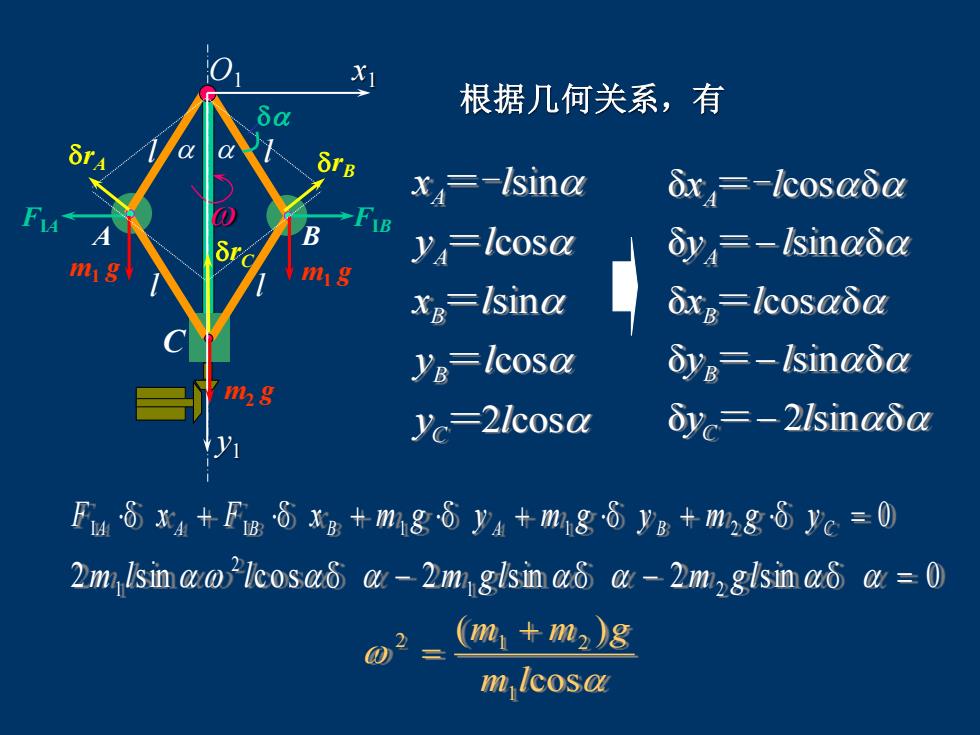
根据几何关系,有 sin cos sin cos 2 cos A A B B C x l y l x l y l y l =- = = = = δ cos δ δ sin δ δ cos δ δ sin δ δ 2 sin δ A A B B C x l y l x l y l y l − − − =- = = = = 2 sin co s δ 2 sin δ 2 sin δ 0 1 2 2 1 m l l − m g l − m g l = cos ( ) 1 2 1 2 m l m + m g = δ δ δ δ δ 0 I I 1 1 2 + + + + = A A B B A B C F x F x m g y m g y m g y C l l l l O1 x1 y1 A B FIA FIB m1 g m1 g m2 g rB rA rC
例题2 质量为m,的三棱柱ABC通过滚 轮搁置在光滑的水平面上。质量 为m2、半径为R的均质圆轮沿三棱 柱的斜面AB无滑动地滚下。 D 求:1、三棱柱后退的加 速度41; 2、圆轮质心C,相对于三 C 棱柱加速度a,。 99w9元
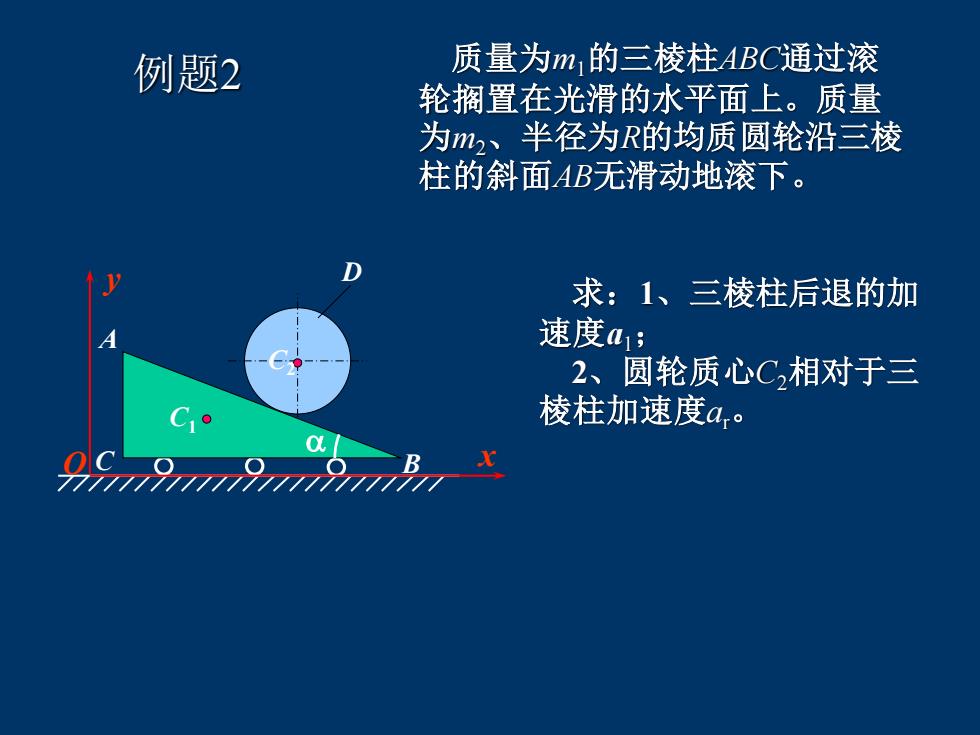
例题2 质量为m1的三棱柱ABC通过滚 轮搁置在光滑的水平面上。质量 为m2、半径为R的均质圆轮沿三棱 柱的斜面AB无滑动地滚下。 求:1、三棱柱后退的加 速度a1; 2、圆轮质心C2相对于三 棱柱加速度ar。 x y C2 D C1 A C B O