同济大学：《理论力学》课程教学课件（PPT讲稿）第三章 刚体力学 §3.1 刚体运动的分析 §3.2 角速度矢量 §3.3 欧拉角

第三章 刚体力学

第三章 刚 体 力 学

刚体学习方法 类比法 - M d d a F=ma M=JB m -Jo M dA=F.dr dA Mde P mv i=J而

刚体学习方法 类比法 p L F M m J a v                           P mv L J dA F dr dA Md E m v E J F ma M J dt dL M dt dp F k r k = = =  = = = = = = = 2 1 2 1 2 2

导读 ·刚体运动分类：平动、转动 ·角位移、角速度矢量 ·欧勒角和欧勒运动学方程

导读 • 刚体运动分类：平动、转动 • 角位移、角速度矢量 • 欧勒角和欧勒运动学方程

§3.1刚体运动的分析 刚体： 形状和大小都不变的物体 任意两质点之间的距离保持不变的质点系

形状和大小都不变的物体 任意两质点之间的距离保持不变的质点系 刚体： §3.1 刚体运动的分析

1平动：刚体在运动过程中，其上任意两点的连线始 终保持平行.可以用一个质点的运动来描述刚体的 平动. 刚体平动>质点运动

1 平动: 刚体在运动过程中, 其上任意两点的连线始 终保持平行. 可以用一个质点的运动来描述刚体的 平动. 刚体平动 质点运动

2转动：刚体上所有质点都绕同一直线作圆周运动.这 条直线称为转轴 转动由转轴位置参量和圆周运动参数来描述。 3:定轴转动：转轴固定不动的转动， 111早1 转轴上的质点不动.只需一个量描述刚体绕该 66 轴转动的角度，就确定了刚体的位置（一个变量）

2 转动: 刚体上所有质点都绕同一直线作圆周运动. 这 条直线称为转轴. 3: 定轴转动： 转轴固定不动的转动. 转轴上的质点不动. 只需一个量描述刚体绕该 轴转动的角度, 就确定了刚体的位置(一个变量). 转动由转轴位置参量和圆周运动参数来描述

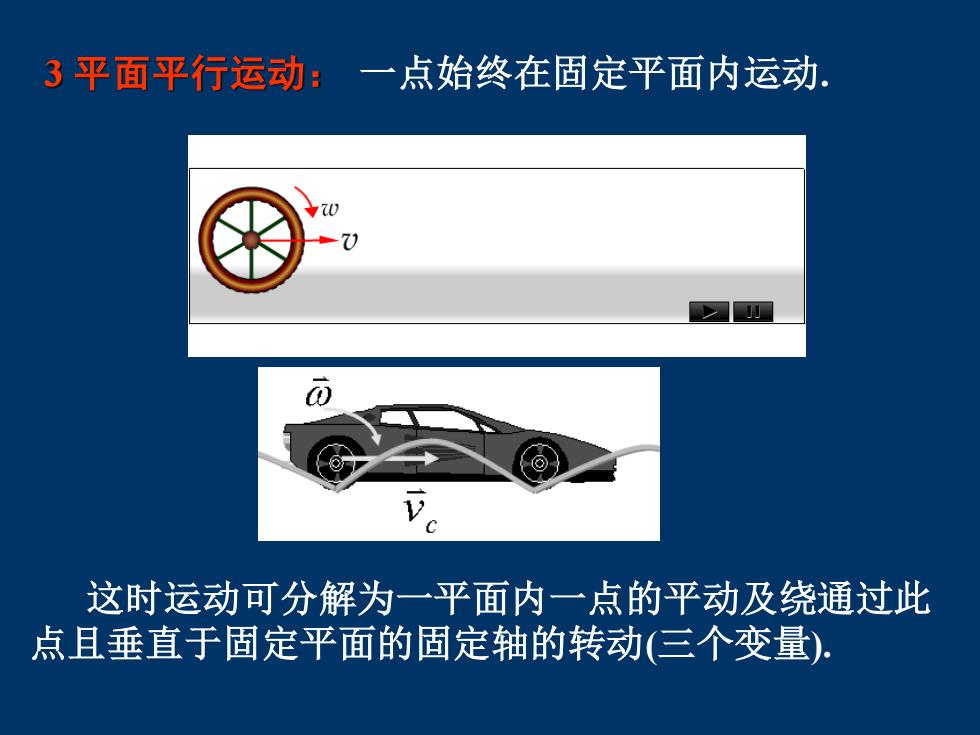
3平面平行运动：一点始终在固定平面内运动： 这时运动可分解为一平面内一点的平动及绕通过此 点且垂直于固定平面的固定轴的转动（三个变量）

3 平面平行运动： 一点始终在固定平面内运动. 这时运动可分解为一平面内一点的平动及绕通过此 点且垂直于固定平面的固定轴的转动(三个变量)

4定点转动：一点固定不动，刚体围绕过这点的某 瞬时轴转动（三个变量）， 陀螺

4 定点转动：一点固定不动, 刚体围绕过这点的某一 瞬时轴转动(三个变量)

5一般运动：刚体不受任何约束，可以在空间任意运动 质心的平动 绕质心的转动

5 一般运动：刚体不受任何约束，可以在空间任意运动. 质心的平动 + 绕质心的转动

§3.2角速度矢量 1有限转动与无限小转动 角坐标 0=θ(t) 约定 沿逆时针方向转动0>0 沿顺时针方向转动0<0 角位移 △0=θ(t+△t)-θt) 当刚体围绕固定点转动时，转动轴方向也是时间的 函数，这时角位移不是矢量

 x z P §3.2 角速度矢量 角位移  =(t + t) −(t) 角坐标  = (t)  0 约定 沿逆时针方向转动 沿顺时针方向转动 1 有限转动与无限小转动 当刚体围绕固定点转动时，转动轴方向也是时间的 函数，这时角位移不是矢量