《结构力学》课程教学资源（PPT课件讲稿）第6章 结构位移计算与虚功——能量法简述

第6章 结构位移计算与虚功-能量法简述 6-1变形体虚功原理 6-2 变形体虚功原理的应用 6-3 刚体虚功原理的应用 6-4互等定理

第6章 结构位移计算与虚功-能量法简述 6-1 变形体虚功原理 6-2 变形体虚功原理的应用 6-3 刚体虚功原理的应用 6-4 互等定理

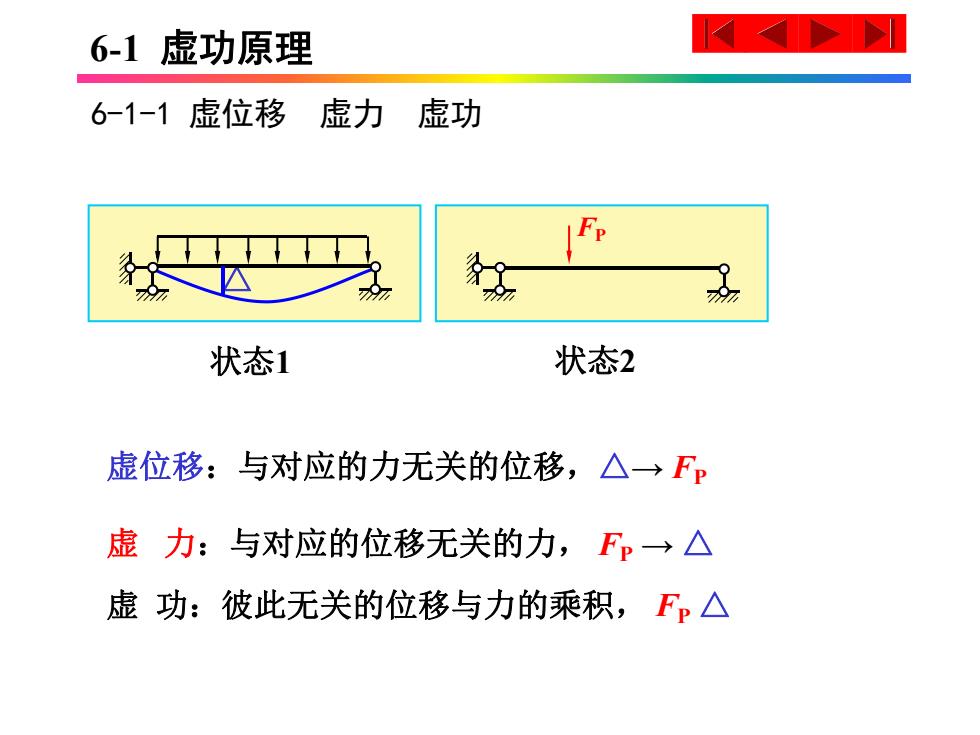
6-1虚功原理 6-1-1虚位移虚力虚功 Fp 状态1 状态2 虚位移：与对应的力无关的位移，△→F。 虚力：与对应的位移无关的力，F,→△ 虚功：彼此无关的位移与力的乘积，Fp△

6-1 虚功原理 6-1-1 虚位移 虚力 虚功 虚位移：与对应的力无关的位移，△→ FP 虚 力：与对应的位移无关的力， FP → △ 虚 功：彼此无关的位移与力的乘积， FP △ △ FP 状态1 状态2

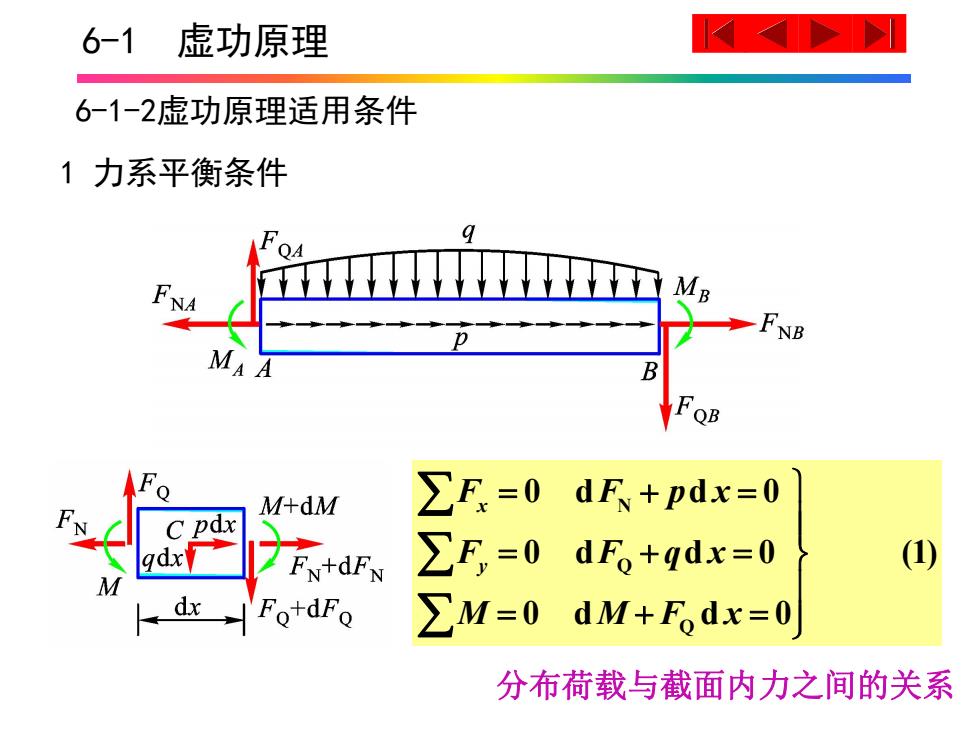
6-1虚功原理 6-1-2虚功原理适用条件 1力系平衡条件 FNA MB FNB MA A B F B M+dM ∑F=0dF+pdx=0 C pdx qdx FN+dFN ∑F=0dF+qdx=0 () M dx Fo+dFo ∑M=0dM+F。dx=0 分布荷载与截面内力之间的关系

6-1 虚功原理 6-1-2虚功原理适用条件 1 力系平衡条件 分布荷载与截面内力之间的关系 N Q Q 0 d d 0 0 d d 0 (1) 0 d d 0 x y F F p x F F q x M M F x                 

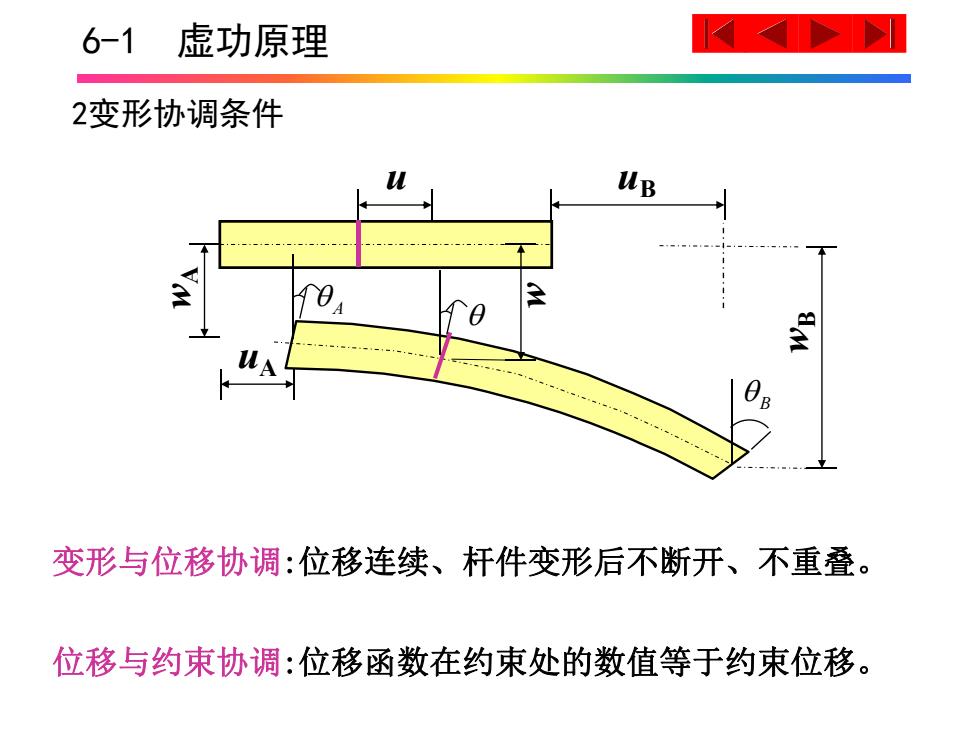
6-1虚功原理 2变形协调条件 uB 变形与位移协调：位移连续、杆件变形后不断开、不重叠。 位移与约束协调：位移函数在约束处的数值等于约束位移

6-1 虚功原理 2变形协调条件 w A uA  A uB  B w B u  w 变形与位移协调:位移连续、杆件变形后不断开、不重叠。 位移与约束协调:位移函数在约束处的数值等于约束位移

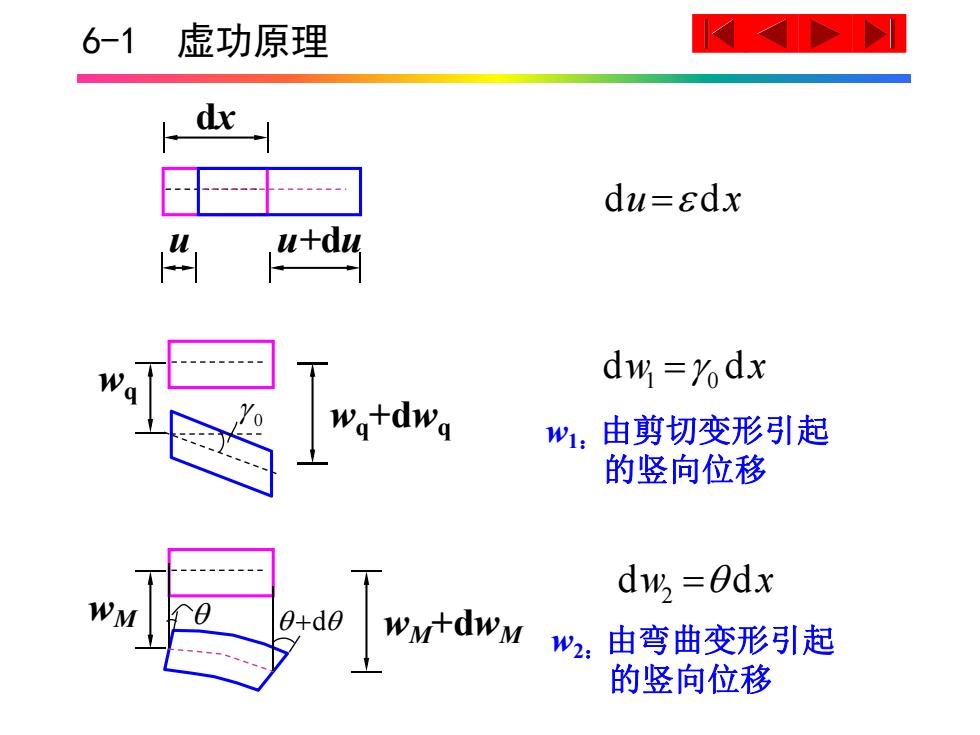
6-1虚功原理 dx du=sdx u+du dw=7dx w1,由剪切变形引起 的竖向位移 dw =0dx 由弯曲变形引起 的竖向位移

6-1 虚功原理 wM+dwM wM   d wq wq+dwq 0  dx u u+du du  dx 1 0 dw  dx w1：由剪切变形引起 的竖向位移 2 dw  dx w2：由弯曲变形引起 的竖向位移

6-1虚功原理 6-1-2变形体虚功原理的证明 由力的平衡方程： dF+pdx=0 dFo+qdx=0 (a) 得 dM+Fodx=0 J【(dF+pdv+(dE+qdew+%)+dM+EdA=0. 将含有“dr”的项合并，得 [ludF++d+dM++FOdx=0

6-1 虚功原理 6-1-2 变形体虚功原理的证明 N Q Q d d 0 d d 0 (a) d d 0 F p x F q x M F x        B N A u F w w F M pu q w w F x 1 2 Q 1 2 Q [ d (  )d d ][  (  ) ]d 0 (c)   将含有“dx”的项合并，得 由力的平衡方程： N Q 1 2 Q [(d d ) (d d )( ) (d d ) ] 0 (b) B A F  p x u F q x w w  MF x    得

6-1 虚功原理 根据公式 d(uw)=udw+wdu 得 duF+(w+%)E+θM☑ =[udFy+w+w)dFo+edM+[Fy du+Fod(w+w)+Mde (c)式积分号中第一项 代入式（c),得 dluFx+(+w)F+OM]-Fxdu+F d(w+w)+MdO]dx +∫pw+gw+wldc+∫iF0dx=0 D .(d

6-1 虚功原理 根据公式 1 2 1 2 Q Q Q 1 2 d[ ] [ d d ( ) ( ) d ] [ d d( ) d ] N N N F F M F F M u w w u w w F u F w w M               （c）式积分号中第一项 代入式（c），得 1 2 Q Q 1 2 1 2 Q d[ ( ) ] [ d d( ) d ] ( d [ )]d d 0 (d) B B N N A A B B A A uF w w F M F u F w M x p q x F x w u w w                     d(uw)=udw+wdu 得

6-1虚功原理 将式(d)第一项积分号去掉，得 Lu++%)E+M-∫n区du+Edg+%)+Ma8dx +ldx+F0dx-0 (e) 将式()第一项上下限代入，并考虑w=%+, d%=0dx,得 [FSBU+FoBWs+Mg0el-IFu+Fow+Mel B +(pdxu+(qdx)w=∫(du+Eodw+Md0.田

6-1 虚功原理 将式（d）第一项积分号去掉，得 1 2 Q Q 1 Q 2 1 2 [ ( ) ] [ d d( ) d ] ( ) d [ ]d d 0 (e) B B N N A A B B A A F F M F F M x p u w w u w w u q w w x F x                    ( d ) ( d ) B A  p x u q x w  N Q N Q [ ] [ ] F BuB F BwB MB B F AuA F AwA MA A        N Q 1 ( d d d ) (f) B A  F uF w  M    将式（e）第一项上下限代入，并考虑 ww1 w2， dw2 dx ，得

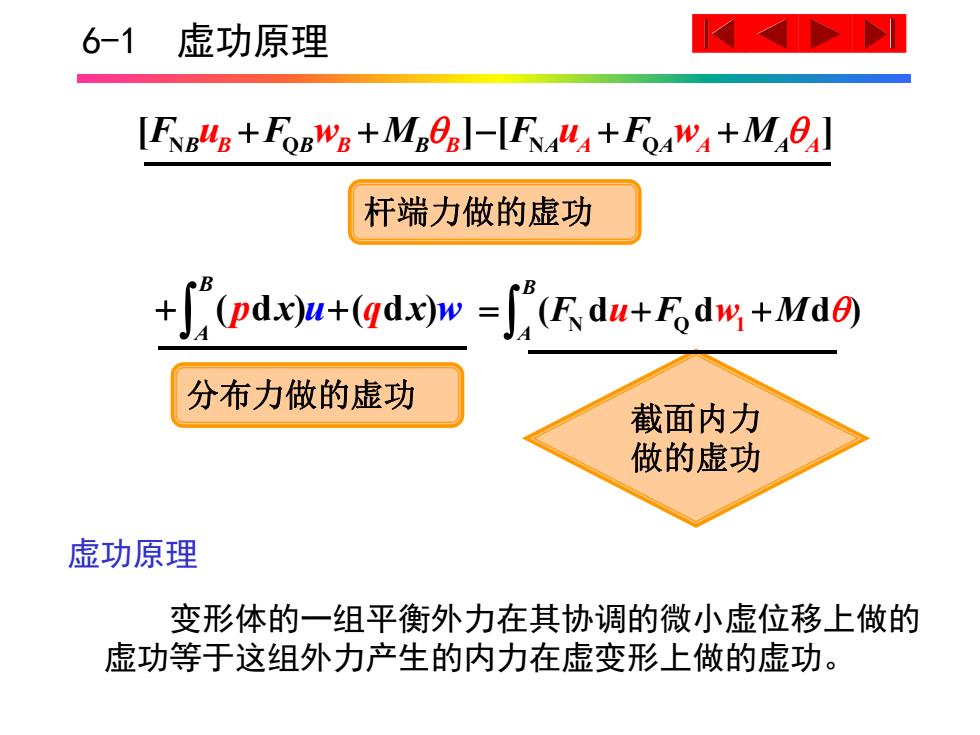
6-1虚功原理 [FNBUB+FoRWg+Mgeel-[Fu+Fow+Mel 杆端力做的虚功 +S(pdx)u+(qdx)w="(Fdu+Fadw,+Md0) 分布力做的虚功 截面内力 做的虚功 虚功原理 变形体的一组平衡外力在其协调的微小虚位移上做的 虚功等于这组外力产生的内力在虚变形上做的虚功

6-1 虚功原理 ( d ) ( d ) B A  p x u q x w  N Q N Q [ ] [ ] F BuB F BwB MB B F AuA F AwA MA A        N Q 1 ( d d d ) B A  F uF w  M   杆端力做的虚功 分布力做的虚功 截面内力 做的虚功 虚功原理 变形体的一组平衡外力在其协调的微小虚位移上做的 虚功等于这组外力产生的内力在虚变形上做的虚功

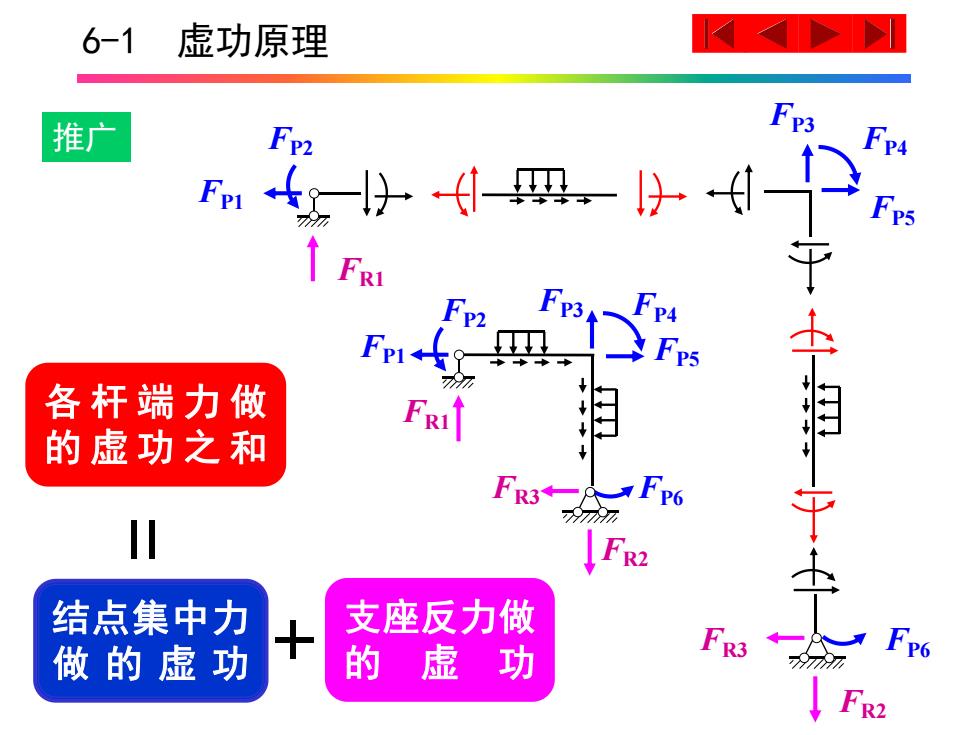
6-1 虚功原理 推广 P3 F4。l以.小 FRI 各杆端力做 的虚功之和 FR3 结点集中力 支座反力做 做的虚功 的虚功 FR2

6-1 虚功原理 FR1 FP1 FP2 FP3 FP4 FP5 FR2 FR3 FP6 FP1 FP2 FP3 FP4 FP5 FP6 FR1 FR2 FR3 推广 支座反力做 的 虚 功 各 杆 端 力 做 的 虚 功 之 和 结点集中力 做 的 虚 功