
第二章 质点组力学
第二章 质点组力学

§2.5两体问题 导读 ·两体问题 ·开普勒定律的修正 ·折合质量
导读 • 两体问题 • 开普勒定律的修正 • 折合质量 §2.5 两体问题

两体问题:两个物体也就是两个质点组成的系统,它 们彼此以内力相互作用,不受外力作用。 例如:单个行星绕太阳的运动;粒子受原子核的散 射等。 以前,假定引力中心太阳是固定不动的,实际上,太 阳不是固定的,它在行星对它的引力作用下也在运动 的。 所以行星并不是在“静止”的力心作用下运动,而 应当考虑太阳和行星都在对方的引力作用下运动
两体问题:两个物体也就是两个质点组成的系统,它 们彼此以内力相互作用,不受外力作用。 例如:单个行星绕太阳的运动;α粒子受原子核的散 射等。 以前,假定引力中心太阳是固定不动的,实际上,太 阳不是固定的,它在行星对它的引力作用下也在运动 的。 所以行星并不是在“静止”的力心作用下运动,而 应当考虑太阳和行星都在对方的引力作用下运动

采用质点组质心系就可以准确求解这个问题。 S:太阳,P:行星,对一个惯性坐标系, 因为引力是内力,所以太阳和行星 S r2 C 组成的系统动量守恒,其质心是相 对惯性系匀速运动的.我们在质心 系中研究太阳和行星的运动: 行星对质心C:m GMm 因C是质心, mr Mr
采用质点组质心系就可以准确求解这个问题. S:太阳, P:行星, 对一个惯性坐标系, 因为引力是内力,所以太阳和行星 组成的系统动量守恒,其质心是相 对惯性系匀速运动的. 我们在质心 系中研究太阳和行星的运动. x y z P S C rs rp rC r2 r1 行星对质心C: ( ) 1 1 2 1 2 1 r r r r GMm mr + = − 因C是质心, 1 2 mr Mr =

GM'm .mr (M+m 力仍与距离平方成反比,从而行星绕质心作圆锥曲 线运动.同理,太阳也是这样。 在惯性坐标系太阳的运动:标- GMm r r r 行星的运动:m=-,产 GMm F 两式加权合并,考虑。-了=开
力仍与距离平方成反比,从而行星绕质心作圆锥曲 线运动.同理,太阳也是这样. ( ) 3 1 1 2 3 1 r r M m GM m mr + = − 在惯性坐标系太阳的运动: r r r GMm Mrs 2 = 行星的运动: r r r GMm mrP 2 = − 两式加权合并, 考虑 r r r P s − =

G(M+m) 得到: mr= 这是行星相对太阳的动力学方程.如认为太阳不动,但 质量增大到了M+m,这时2=GM+m对不同行星不一 样,所以开普勒定律需要修正. 对行星P1 4ra=GM+m) 对行星P2 4r2a=GM+m) 02 =(M+m)(M+,) T)
( ) r r m r G M m mr 2 + 得到: = − 这是行星相对太阳的动力学方程. 如认为太阳不动, 但 质量增大到了M+m, 这时k 2 =G(M+m)对不同行星不一 样, 所以开普勒定律需要修正. 对行星P1 ( ) 2 1 1 3 1 2 4 G M m a = + 对行星P2 ( ) 2 2 2 3 2 2 4 G M m a = + ( ) ( ) 2 1 2 2 3 2 2 1 3 1 : M m : M m a a = + +

a 1+ M 1+ M 最大的木星 M 1047 开普勒给出的等式右边是1,所以开普勒是近似的
M m M m a a 2 1 2 2 3 2 2 1 3 1 1 1 : + + = 开普勒给出的等式右边是1, 所以开普勒是近似的. 最大的木星 1047 1 1 = M m

如果我们改写mi-G+四m2为 Mm GM -1n M+m 其中u=Mm/M+m)叫做折合质量. 这时可以看作行星的质量改变,而还是围绕不动的太 阳运行
( ) r r m r G M m mr 2 + 如果我们改写 = − 为 r r m r GM r r M m Mm 2 = = − + 其中 =Mm/(M+m)叫做折合质量. 这时可以看作行星的质量改变,而还是围绕不动的太 阳运行

小结 1两物体相互在引力作用下运动时,每一个物体绕两 者的质心作圆维曲线运动,而质心作惯性运动. 2把一物体看做不动,而把另一物体看成绕它作圆锥 曲线运动,可在利用动力学方程时视后者的质量减少 到4=Mm/(M什m)-折合质量. 3开普勒第三定律的修正 1+ m M 1+ 1m2 M
小 结 1 两物体相互在引力作用下运动时,每一个物体绕两 者的质心作圆锥曲线运动,而质心作惯性运动. 2 把一物体看做不动, 而把另一物体看成绕它作圆锥 曲线运动, 可在利用动力学方程时视后者的质量减少 到 =Mm/(M+m) -折合质量. 3 开普勒第三定律的修正 M m M m a a 2 1 2 2 3 2 2 1 3 1 1 1 : + + =
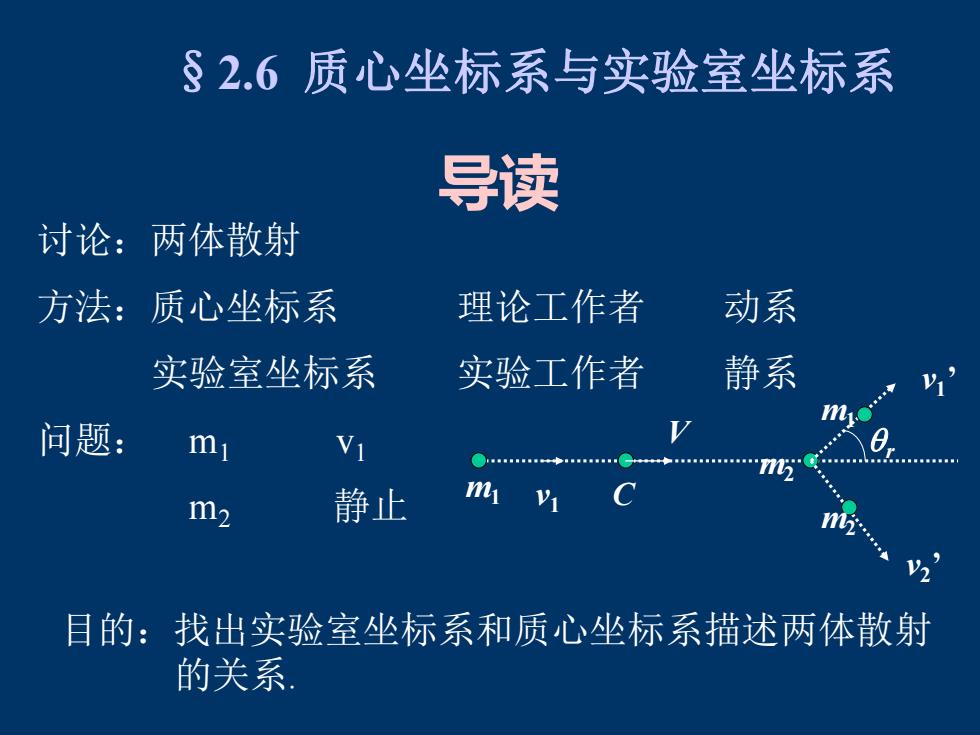
§2.6质心坐标系与实验室坐标系 导读 讨论:两体散射 方法:质心坐标系 理论工作者 动系 实验室坐标系 实验工作者 静系 问题: ● m2 静止 1 目的:找出实验室坐标系和质心坐标系描述两体散射 的关系
讨论:两体散射 方法:质心坐标系 理论工作者 动系 实验室坐标系 实验工作者 静系 问题: m1 v1 m2 静止 目的:找出实验室坐标系和质心坐标系描述两体散射 的关系. m1 v1 ’ m2 m1 v2 ’ C r m2 v1 V §2.6 质心坐标系与实验室坐标系 导读