
第二章 质点组力学
第二章 质点组力学

§2.3动量矩定理与动量矩守恒律 导读 ·类比法 ·力矩、冲量矩、角动量 ·质点对固定点、固定轴的动量矩定理 ·动量矩守恒定律 ·对质心的动量矩定理 F→M P-5 →M- p→i dt dt
导 读 • 类比法 • 力矩、冲量矩、角动量 • 质点对固定点、固定轴的动量矩定理 • 动量矩守恒定律 • 对质心的动量矩定理 p L F M → → t L M t p F d d d d = → = §2.3 动量矩定理与动量矩守恒律
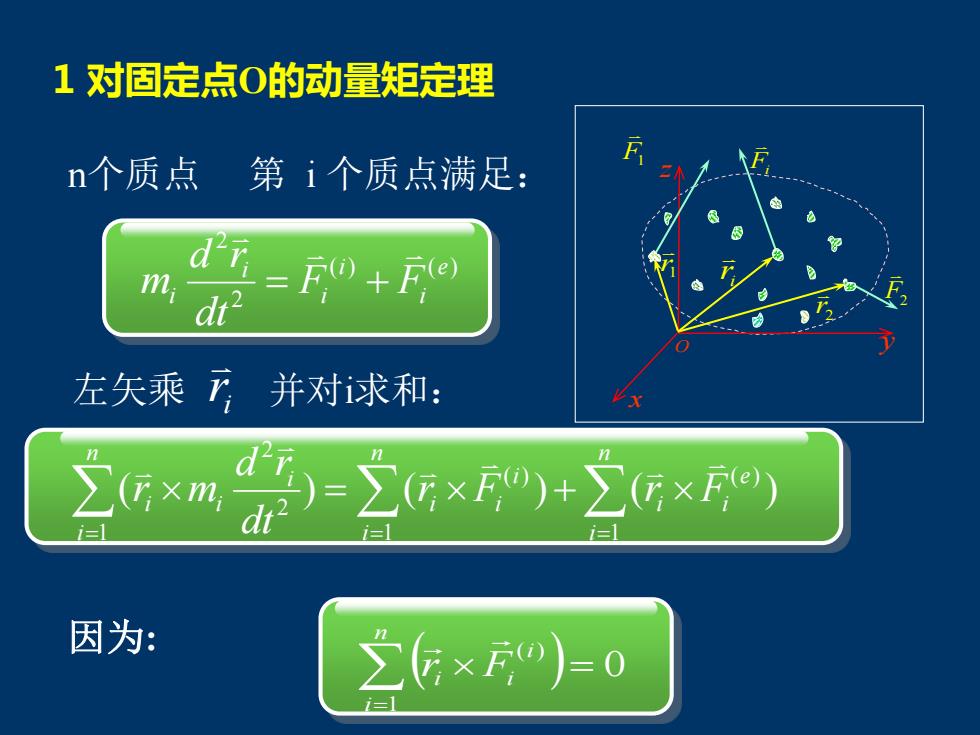
1对固定点O的动量矩定理 n个质点第i个质点满足: d'n=+F m dt 左矢乘下并对求和: -2G×9+2 i= 因为: 36×F0)=0
1 对固定点O的动量矩定理 ( ) ( ) 2 2 e i i i i i F F dt d r m = + i r = = = = + n i e i i n i i i i n i i i i r F r F dt d r r m 1 ( ) 1 ( ) 1 2 2 ( ) ( ) ( ) 左矢乘 并对i求和: n个质点 第 i 个质点满足: ( ) 0 1 ( ) = = n i i i Fi r 因为: O x y z 1 r i r 2 r F1 F2 Fi

m兽-2密xm岛立) d - 7=之6×FJ=G×m)-空G×p》 所以仍有: M- d.J dt
= = = n i e i i n i i i i r F dt dr r m dt d 1 ( ) 1 ( ) ( ) = = = = + n i i i i n i i i i n i i i i dt d r r m dt dr m dt dr dt dr r m dt d 1 2 2 1 1 ( ) ( ) ( ) dt dJ M = ( ) ( ) ( ) = = = = = = n i i i n i i i i n i e M ri Fi J r m v r p 1 1 1 ( ) , 所以仍有:

质点组对固定点的动量矩定理: =M dt 意义:质点组对任一固定点的动量矩对时间的 微商等于诸外力对同一点的力矩的矢量和
质点组对固定点的动量矩定理: M dt dJ = 意义:质点组对任一固定点的动量矩对时间的 微商等于诸外力对同一点的力矩的矢量和

分量式: 公m0空x) d)) 孟空网-芝
分量式: ( ) ( ) ( ) 1 ( ) 1 e i i y n i e i i z n i mi yi zi zi yi y F z F dt d = = − = − ( ) ( ) ( ) 1 ( ) 1 e i i z n i e i i x n i mi zi xi xi zi z F x F dt d = = − = − ( ) ( ) ( ) 1 ( ) 1 e i i x n i e i i y n i mi xi yi yi xi x F y F dt d = = − = −

2动量矩守恒 ·若M=0则j=c 意义:质点组不受外力作用时或虽受外力作用,但这 些对某定点的力矩的矢量和为0,则对此定点而言, 质点组动量矩为一横矢量 若对某一通过定点的定轴的力矩为0 M=0则J=∑my,-)-e 动量矩守恒定律是自然界的一条普遍定 律,它有着广泛的应用
2 动量矩守恒 意义:质点组不受外力作用时或虽受外力作用,但这 些对某定点的力矩的矢量和为0,则对此定点而言, 质点组动量矩为一横矢量. M = 0 J c = Mx = 0 则 J m y z z y c n i x i i i i i = = − = 1 ( ) • 若 则 若对某一通过定点的定轴的力矩为0 动量矩守恒定律是自然界的一条普遍定 律,它有着广泛的应用

3对质心的角动量定理: n个质点,P是任一质点,质量为m C是质心.坐标系O-xyz是固定系, 另有C-xy'z'系,原点在质心C,随C 相对于O-xyz平动.对运动参考系 d=e+f0+(-m) m
3 对质心的角动量定理 : n个质点, Pi是任一质点 ,质量为 m i , C是质心. 坐标系 O -xyz是固定系, 另有 C-x’y’z’ 系, 原点在质心 C, 随 C 相对于 O -xyz平动. 对运动参考系 x y z ri r Cri ’ Pi C O ( ) dd ' ( ) ( ) 2 2 i C i i e i i i F F m r tr m = + + −

dm]-立立m ∑m,=0 m当]-之w 对质心的角动量定理: =M dt
= = = = + n i C i i e i n i i n i i i i r F r m r t r r m t 1 ( ) 1 1 ' ' d d ' ' d d ' 0 1 = = n i i i m r ( ) 1 1 ' d d ' ' d d e i n i i n i i i i r F t r r m t = = = 对质心的角动量定理: ' ' M dt dJ =

d 对质心的角动量定理: =M 意义:质点组对质心c的动量矩对时间的微商 等于所有外力对质心的力矩之后 注意: 虽然质心是动点,但是角动量定理和对固定点形 式一样但是对其他任意动点由于不满足 ∑m,f'=0 则不能得出这样的角动量定理形式
对质心的角动量定理: 虽然质心是动点, 但是角动量定理和对固定点形 式一样.但是对其他任意动点由于不满足 则不能得出这样的角动量定理形式. ' 0 1 = = n i i i m r ' ' M dt dJ = 意义:质点组对质心c的动量矩对时间的微商 等于所有外力对质心的力矩之后. 注意: