同济大学：《理论力学》课程教学课件（PPT讲稿）第三章 刚体力学 §3.7 刚体的平面平行运动

第三章 刚体力学

第三章 刚 体 力 学

§3.7刚体的平面平行运动 导读 ·刚体平面平行运动的运动学 ·刚体平面平行运动的动力学 ·刚体平面平行运动时相对于质心的角动量定理 ·刚体平面平行运动时机械能守恒律

导读 • 刚体平面平行运动的运动学 • 刚体平面平行运动的动力学 • 刚体平面平行运动时相对于质心的角动量定理 • 刚体平面平行运动时机械能守恒律 §3.7 刚体的平面平行运动

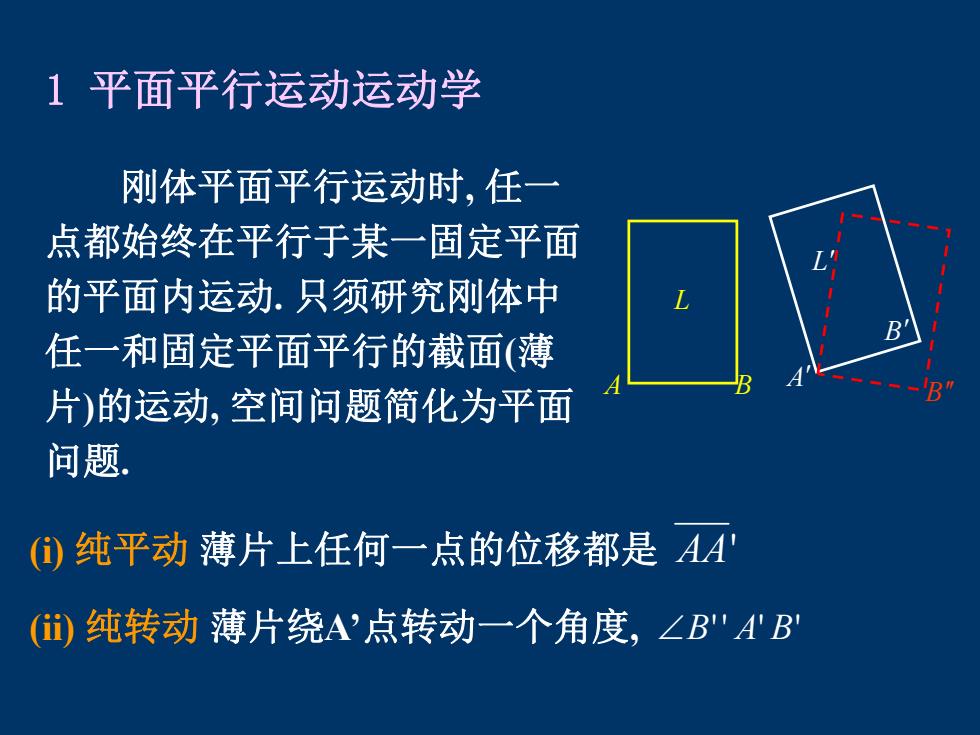
1平面平行运动运动学 刚体平面平行运动时，任一 点都始终在平行于某一固定平面 的平面内运动.只须研究刚体中 任一和固定平面平行的截面（薄 片)的运动，空间问题简化为平面 问题. ①纯平动薄片上任何一点的位移都是AA ()纯转动薄片绕A'点转动一个角度，∠B"AB

1 平面平行运动运动学 刚体平面平行运动时, 任一 点都始终在平行于某一固定平面 的平面内运动. 只须研究刚体中 任一和固定平面平行的截面(薄 片)的运动, 空间问题简化为平面 问题. (i) 纯平动 薄片上任何一点的位移都是 AA' (ii) 纯转动 薄片绕A’点转动一个角度, B' ' A' B' A B A B B L L

薄片上一点速度，加速度 :-0 - ）-(- A点加速度 相对切向加速度相对向心加速度 A点常叫基点 2转动瞬心 任一时刻薄片上恒有一点速度为零，叫做转动瞬心(C), 转动瞬心相对于Oxy系的坐标可从上式求得 eX0e乃+

薄片上一点速度, 加速度   0 v v r ' v r r A A                      2 a a A  r r0 r r0                A点加速度 相对切向加速度 相对向心加速度 A点常叫基点 任一时刻薄片上恒有一点速度为零, 叫做转动瞬心(C), 转动瞬心相对于Oxy系的坐标可从上式求得   Ax C Ay C v y y v x  x0  ,  0        x  y  x y P , , r r  0r z x y x  y  z  A v O 

如果0=0，则无转动瞬心，或者说，转动瞬心在无穷远 处， 只要转动瞬心C已知，就知道薄片在此时的运动.因为 如果取C为基点，则因它此时的速度为零，薄片将仅绕C 转动而任意一点P的速度大小为CP0 过A及B作两直线分别垂直于 VA及y,此两直线的交点即为 转动瞬心

如果＝0, 则无转动瞬心, 或者说, 转动瞬心在无穷远 处. 只要转动瞬心C已知,就知道薄片在此时的运动.因为 如果取C为基点，则因它此时的速度为零,薄片将仅绕C 转动而任意一点P 的速度大小为 CP  过A及B作两直线分别垂直于 vA及vB, 此两直线的交点即为 转动瞬心. A B C A v B v

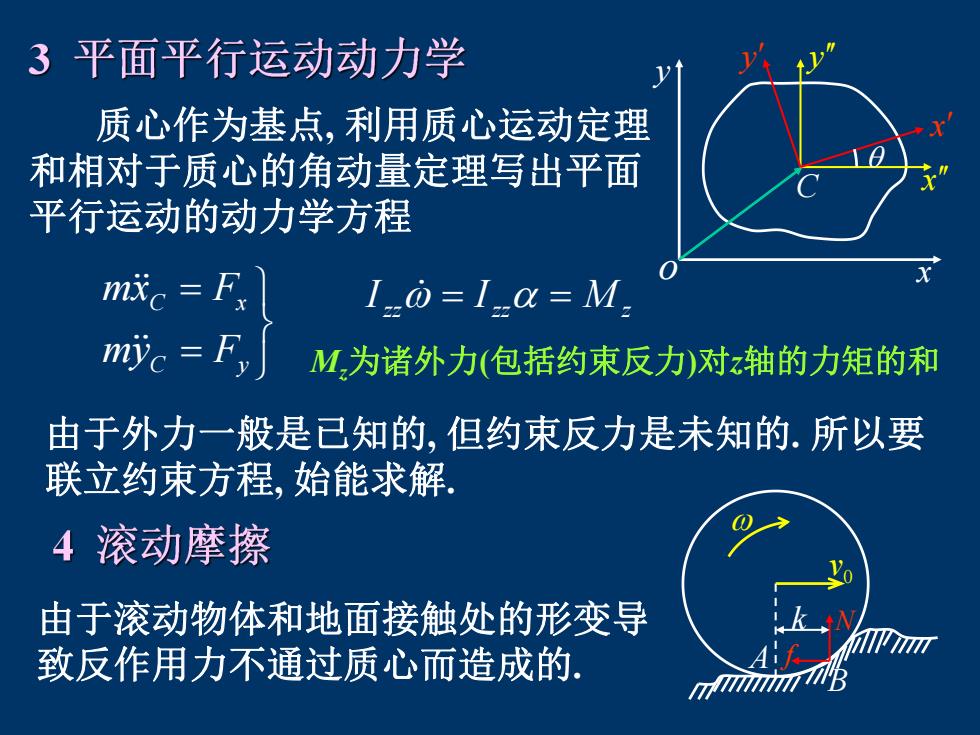
3平面平行运动动力学 y 质心作为基点，利用质心运动定理 和相对于质心的角动量定理写出平面 平行运动的动力学方程 m成=F I.=1a=M. myc Fy M为诸外力（包括约束反力）对z轴的力矩的和 由于外力一般是已知的，但约束反力是未知的.所以要 联立约束方程，始能求解。 4滚动摩擦 由于滚动物体和地面接触处的形变导 致反作用力不通过质心而造成的

质心作为基点, 利用质心运动定理 和相对于质心的角动量定理写出平面 平行运动的动力学方程      C y C x my F mx F   zz zz M z I   I   Mz为诸外力(包括约束反力)对z轴的力矩的和 由于外力一般是已知的, 但约束反力是未知的. 所以要 联立约束方程, 始能求解. 由于滚动物体和地面接触处的形变导 致反作用力不通过质心而造成的. x y o C x  x  y  y   f k N A B 0 v 

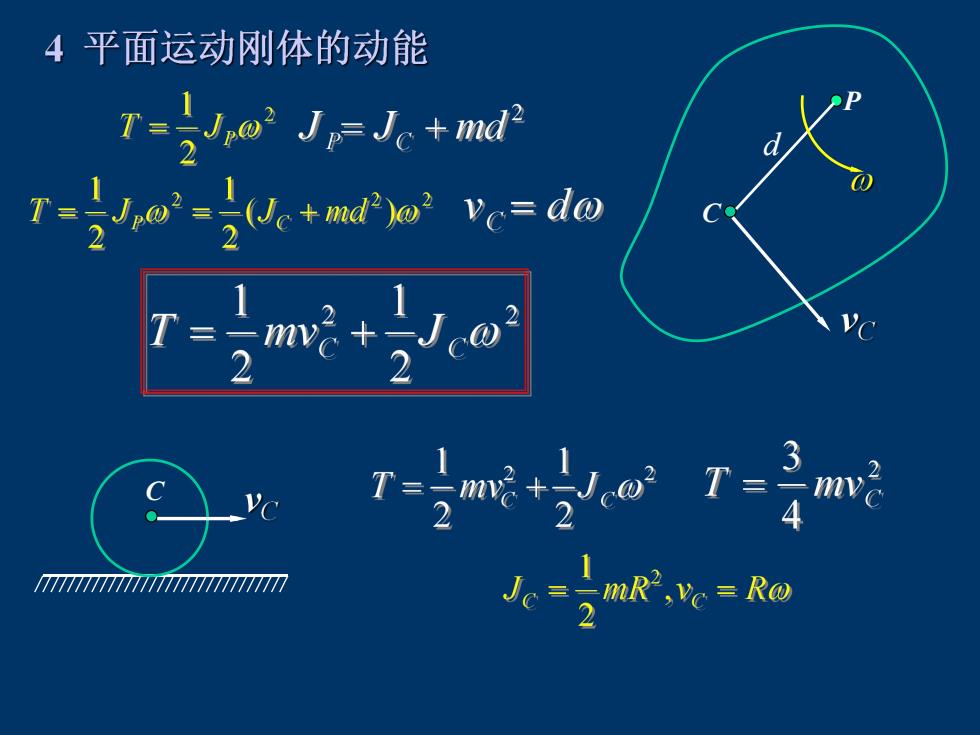
4平面运动刚体的动能 T=+md2 T=(e+md)o2 Vc=d@ T= 7771711777777711111 -mR2,vo=Ro

C P C d

例1如图，将一根质量为m的长杆用 细绳从两端水平地挂起来，其中一根 绳子突然断了，另一根绳内的张力是 多少？ 解：设杆子长2儿，质心运动定理和过质心轴的角动量定 理给出绳断的一刹那的运动方程： mg -T mac Tl=IcB Ic =ml2 因在此时悬绳未断的一端加速度为零，从而有 ac Bl 7 mg

例1 如图, 将一根质量为m的长杆用 细绳从两端水平地挂起来, 其中一根 绳子突然断了,另一根绳内的张力是 多少? T 解: 设杆子长2l, 质心运动定理和过质心轴的角动量定 理给出绳断的一刹那的运动方程: C  C Tl I mg T ma    因在此时悬绳未断的一端加速度为零, 从而有 2 3 I 1 ml C  a l C   T mg 4 1  

例2如图，一半径为R的乒乓球与水平面摩擦系数为山，开 始时，用手按球的上左侧，使球质心以v©向右运动，并具 有逆时针方向的初始角速度o,设yc00,乒乓 球一边滑动，一边倒着转动.它在水 平面方向受滑动摩擦力-mg的作 用，按照质心运动定理，有 -Lmg mac mvcvc vco -ugt (a)

例2 如图, 一半径为R的乒乓球与水平面摩擦系数为. 开 始时, 用手按球的上左侧, 使球质心以vC0向右运动, 并具 有逆时针方向的初始角速度0 , 设vC00, 乒乓 球一边滑动, 一边倒着转动. 它在水 平面方向受滑动摩擦力-mg的作 用, 按照质心运动定理, 有 (a) 0 mg ma mv v v gt    C  C  C  C   vC0 0 t=0 f P P vC t=t1

对质心的摩擦擦力矩-mgR, 对质心的转动方程为 -umgR=Ic0=号mR2o→0=o-3gt/R(b) 利用(a)和b)来分析乒乓球的运动 (1)当t=vc/(4g),Vc-0,o-3vc2R),据条件vc0 0,质心停止运动，绕质心的 旋转方向没有变

利用(a)和(b)来分析乒乓球的运动 / (b) 2 3 0 2 3 2  mgR  IC  mR       gt R vC0 0 t=0 f P P vC t=t1 对质心的摩擦擦力矩-mgR, 对质心的转动方程为 (1) 当t=t1=vC0 /(g), vC=0, =0 – 3vC0 /(2R), 据条件vC0 0, 质心停止运动, 绕质心的 旋转方向没有变