
第三章 刚体力学( 刚体概念,角速度 超卓谋程
第三章 刚体力学 (I) 刚体概念,角速度

导读 ·刚体学习方法 ·刚体运动分类,自由度 ·角位移、角速度矢量 超卓课程
导读 • 刚体运动分类,自由度 • 角位移、角速度矢量 • 刚体学习方法

刚体学习方法—类比法 物理量 物理公式 质点平动 刚体转动 质点平动 刚体转动 M= d 节 dt dt F=ma M=la a a H 2m 1 m 方 M dw =F.dr dw Mdo P=mv j=1ò 思考,哪个量 更重要? 思考:1.你还能写出哪些两者对照的关系式? 2针对第二章的质点系,有哪些对应的关系式? 超卓谋程
刚体学习方法——类比法 质点平动 刚体转动 物理量 质点平动 刚体转动 物理公式 思考,哪个量 更重要? 思考: 1. 你还能写出哪些两者对照的关系式? 2. 针对第二章的质点系,有哪些对应的关系式?

刚体: 任意两质点之间的距离保持不变的质点系 形状和大小都不变的物体 问题: 需要多少个独立变量来描述刚体的运动? 超卓课程
形状和大小都不变的物体 刚体: 任意两质点之间的距离保持不变的质点系 问题: 需要多少个独立变量来描述刚体的运动?

§3.1刚体运动的分析 描述刚体位置的独立变量 确定刚体位置一般需要六个独立变量 确定刚体位置的三种方法 不共线的三个点.不方便 (2)任一点与过该点的一轴线加绕轴线的转角.一般, (3) 三个独立的角度(欧拉角).优. 超卓谋程
§3.1 刚体运动的分析 确定刚体位置的三种方法 (1) 不共线的三个点. (2) 任一点与过该点的一轴线加绕轴线的转角. (3) 三个独立的角度(欧拉角). 不方便. 一般. 优. 1 描述刚体位置的独立变量 确定刚体位置一般需要六个独立变量
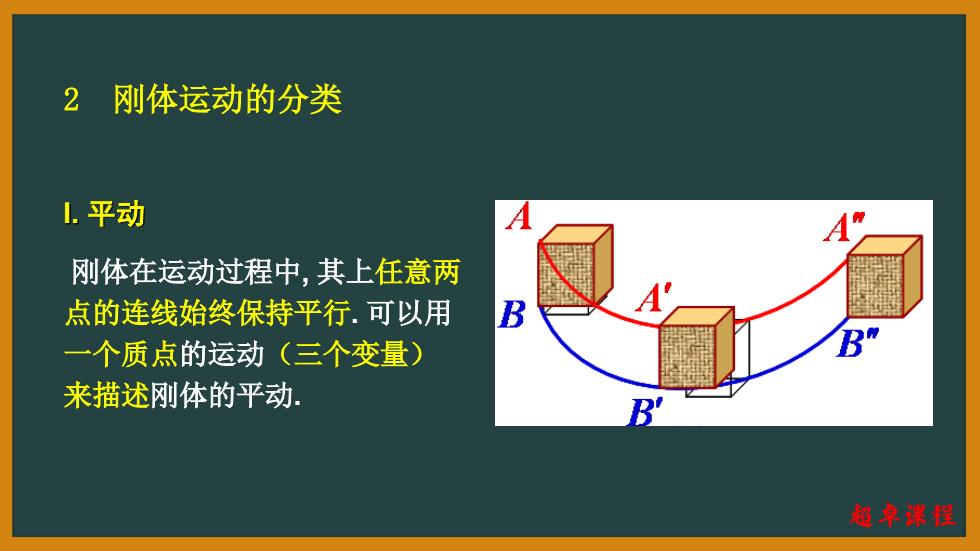
刚体运动的分类 2 1.平动 A 刚体在运动过程中,其上任意两 点的连线始终保持平行.可以用 B 一个质点的运动(三个变量) 来描述刚体的平动. B 超卓课程
I. 平动 刚体在运动过程中, 其上任意两 点的连线始终保持平行. 可以用 一个质点的运动(三个变量) 来描述刚体的平动. 2 刚体运动的分类

l.转动 刚体上所有质点都绕同一直线作圆周运动.这条直线称为转轴 转动由转轴位置参量和圆周运动参数来描述。 定轴转动转轴固定不动的转动, 转轴上的质点不动.只需一个量描述刚体绕该轴 转动的角度,就确定了刚体的位置(一个变量): 超卓谋程
II. 转动 刚体上所有质点都绕同一直线作圆周运动. 这条直线称为转轴. 定轴转动 转轴固定不动的转动. 转轴上的质点不动. 只需一个量描述刚体绕该轴 转动的角度, 就确定了刚体的位置(一个变量). 转动由转轴位置参量和圆周运动参数来描述

山.平面平行运动 重点 一点始终在固定平面内运动: 这时运动可分解为一平面 内一点的平动及绕通过此点 且垂直于固定平面的固定轴 的转动(三个变量). 图3(a) 图3(b) 超卓课程
III. 平面平行运动 一点始终在固定平面内运动. 这时运动可分解为一平面 内一点的平动及绕通过此点 且垂直于固定平面的固定轴 的转动(三个变量). 重点

V.定点转动 重点 一点固定不动,刚体围绕过这点的 某一瞬时轴转动(三个变量). V.一般运动 刚体不受任何约束,可以在空间任意运动 质心的平动 绕质心的转动 超卓谋程
IV. 定点转动 一点固定不动, 刚体围绕过这点的 某一瞬时轴转动(三个变量). V. 一般运动 刚体不受任何约束,可以在空间任意运动. 质心的平动 + 绕质心的转动 重点
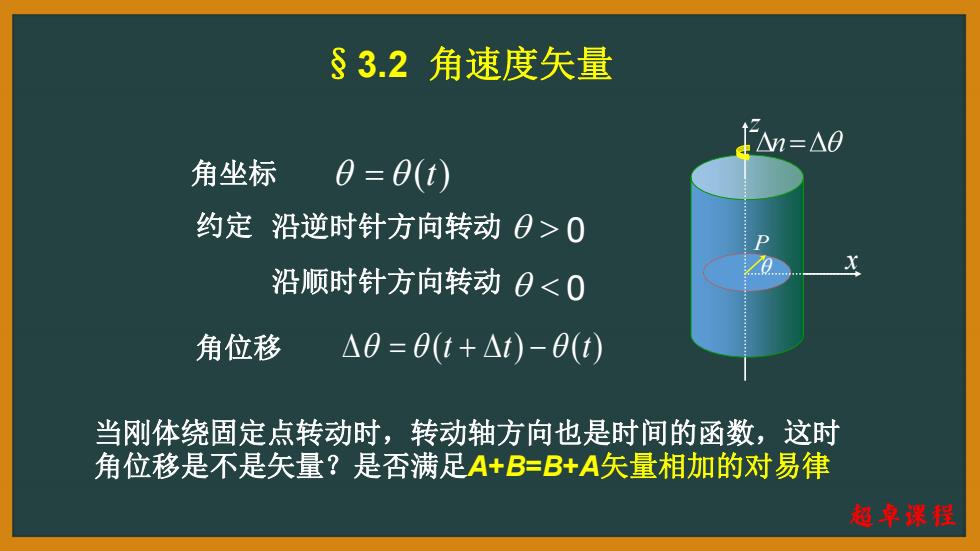
§3.2角速度矢量 =A0 角坐标 0=0(t) 约定 沿逆时针方向转动0>0 沿顺时针方向转动0<0 角位移 △0=0t+△t)-0(t) 当刚体绕固定点转动时,转动轴方向也是时间的函数,这时 角位移是不是矢量?是否满足A+B=B+A矢量相加的对易律 超卓课程
x z P §3.2 角速度矢量 角位移 (t t) (t) 角坐标 (t) 0 沿顺时针方向转动 当刚体绕固定点转动时,转动轴方向也是时间的函数,这时 角位移是不是矢量?是否满足A+B=B+A矢量相加的对易律