中国石油大学（华东）：《理论力学 Theoretical Mechanics》课程教学课件（讲稿）第一章 质点力学——有心力

第一章 质点力学 有心力

第一章 质 点 力 学 有心力

§1.9 有心力 导读 。有心力的性质 比耐公式 ·开普勒定律 。宇宙速度 。 圆形轨道的稳定性 ·粒子散射 。 引力场（补充）

导读 • 有心力的性质 • 比耐公式 • 开普勒定律 • 宇宙速度 • 圆形轨道的稳定性 • 粒子散射 • 引力场(补充) §1.9 有心力

Jupiter Saturn Uranus Mercury Earth Pluto ·●0 Venus Mars Neptune SUN

1.有心力的性质 定义：如果运动质点所受的力的作用线始终通过某一个 定点，这个质点所受的力是有心力.而这个定点则叫做 力心.凡力趋向定点的是引力，离开定点的是斥力 在有心力的作用下，质点始终在一平面内运动.因 力F与位矢r共线r×F=0,L=恒矢量. F=F(r)

1. 有心力的性质 定义: 如果运动质点所受的力的作用线始终通过某一个 定点, 这个质点所受的力是有心力. 而这个定点则叫做 力心. 凡力趋向定点的是引力，离开定点的是斥力． 在有心力的作用下，质点始终在一平面内运动. 因 力F与位矢 r 共线 r × F＝0, L＝恒矢量． r r F F r    ( )

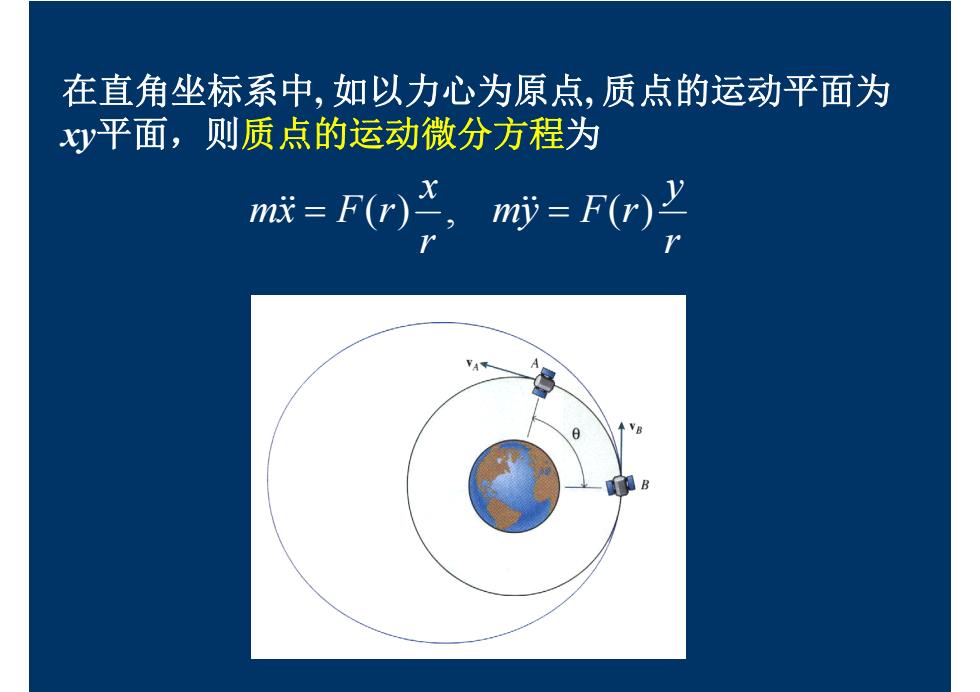
在直角坐标系中，如以力心为原点，质点的运动平面为 xy平面，则质点的运动微分方程为 m=F(r)=F(r)

r y my F r r x mx  F(r) ,   ( ) 在直角坐标系中, 如以力心为原点, 质点的运动平面为 xy平面，则质点的运动微分方程为

)质点的动力学方程（极坐标）为： m(-r02)=F=F(r）(1) mr0+2r0)=F。=0 (2) (2)式又可写为 0o mr20 mh 3) (3)就是角动量守恒定律在极坐标中的表示

i) 质点的动力学方程(极坐标)为: ( 2 ) 0 ( ) ( ) 2           m r r F m r r F F r r      (1) (2) m r v F O h (3)就是角动量守恒定律在极坐标中的表示. (2)式又可写为   0, 1 2    r dt d r m mr   mh  2 (3)

极坐标系中，力做功表达式A=jFdt+rd0 有心方时4jFa了r过 )极坐标系中，机械能守恒表达式： m2+r20）+Vr)=E 有心力是保守力，必定有势能)存在

ii) 极坐标系中, 力做功表达式 A F dr F rd B A   r  有心力时     2 1 d d r r r B A r A F r F r mr  r V(r)  E 2 2 2 2 1    有心力是保守力, 必定有势能V(r)存在 iii) 极坐标系中, 机械能守恒表达式:

2.轨道方程： m-r62)=F,=F(r) () 1 m26-mh 0=hu2 YP= dr dr de 2d/d0=- 1 du=-h du dt d0 di do dt u"2 d0 do = dt do? 从动力学方程中消去时间变量，得 h-u? d'u +u u m 比耐公式

r u m F u u h u 1 , d d 2 2 2 2                2 2 2 2 2 d d d d d d d d d d d d d d d 1 d d d d d 1/ d d d d d d             u h u u h u h t t r r u h u t u u t r t r r                                 从动力学方程中消去时间变量，得 2. 轨道方程: ——比耐公式 2    h r 1       1 2 m r r F F r    r    mr   mh 2 

3.平方反比引力 万有引力、电磁力（有引力、斥力），以引力为例： GMm k2m 2 2=-mk2u2 代入轨道方程，得 du k2 +2u= d02 h2 令 u=5+ 则方程变为 +5=0

3. 平方反比引力 万有引力、电磁力(有引力、斥力), 以引力为例： 2 2 2 2 2 mk u r k m r GMm F       2 2 2 2 2 mk u r k m r GMm F       2 2 2 2 d d h k u u    则方程变为 代入轨道方程，得 2 2 h k 令 u    0 d d 2 2    

这个微分方程和简谐振子方程一样，所以它的解 5=Acos0-0) k2 而 -4e-片月 u=5+ h21k2 Y=- u 1+Acos(0-0)h2/k2 式中A和0，是两个积分常数，令0，=0，轨道简化为 h-1k 1+Ah2/k2 cos0 与标准圆锥方程 相比较，知轨道是原点 1+ecos0 在焦点上的圆锥曲线，力心位于焦点上

  2 2 0 2 2 1 cos / 1 / A h k h k u r        2 2 0 2 2 1 cos / 1 / A h k h k u r      式中A和0是两个积分常数，令0 ＝0，轨道简化为   0   Acos   0   Acos   这个微分方程和简谐振子方程一样，所以它的解 而   2 2 2 0 2 cos h k A h k u        1  / cos / 2 2 2 2 Ah k h k r   1  / cos / 2 2 2 2 Ah k h k r   与标准圆锥方程 1 e cos p r   1 e cos p r   相比较，知轨道是原点 在焦点上的圆锥曲线，力心位于焦点上