
§3.6刚体的平动与定轴转动 导读 ·刚体平动方程 ·定轴转动角动量定理和机械能守恒律 ·定轴转动的轴上附加力 超卓课程《理论力学》
超卓课程《理论力学》 导读 • 定轴转动角动量定理和机械能守恒律 • 定轴转动的轴上附加力 §3.6 刚体的平动与定轴转动 • 刚体平动方程
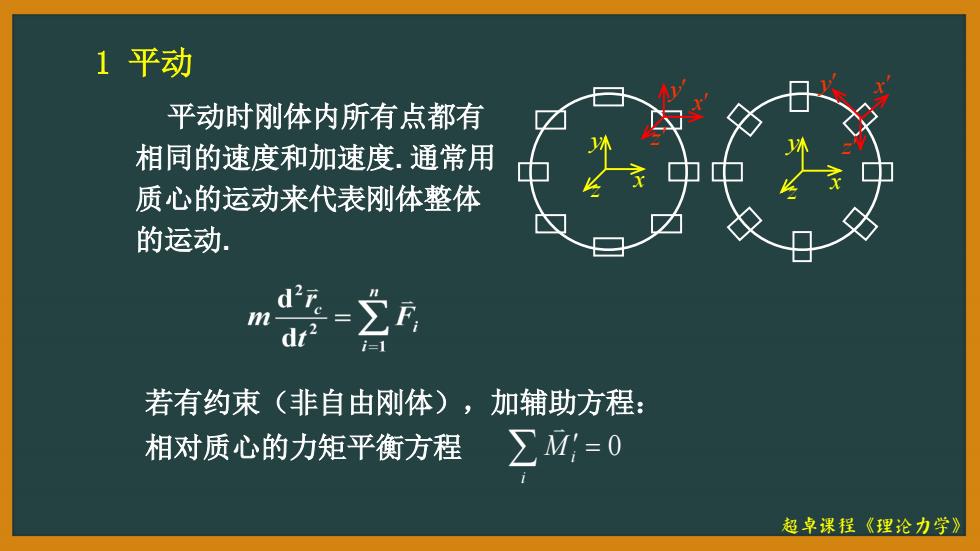
1平动 平动时刚体内所有点都有 相同的速度和加速度.通常用 质心的运动来代表刚体整体 的运动. d2 若有约束(非自由刚体),加辅助方程: 相对质心的力矩平衡方程 ∑M=0 超卓课程《理论力学》
超卓课程《理论力学》 1 平动 平动时刚体内所有点都有 相同的速度和加速度. 通常用 质心的运动来代表刚体整体 的运动. 若有约束(非自由刚体),加辅助方程: 相对质心的力矩平衡方程 0 i M i x y z y x z x y z x y z

2定轴转动 刚体绕固定轴z轴转动时,刚体中任何一点P。都在 垂直于z轴的平面内,作圆周运动,而且到定轴的距离 相等的点的运动完全一样.因此研究刚体的定轴转动, 只要研究与转轴垂直的任意平面内的运动即可其运动 学的独立变量为1. 角量表示: 角位移 0 角速度 角加速度 设一质点的位矢是r,它和z轴距离为R,如果在某一时刻 质点P的线速度为y,则下,=O×F V;=OR 超卓课程《理论力学》
超卓课程《理论力学》 设一质点的位矢是ri , 它和z轴距离为Ri , 如果在某一时刻, 质点Pi的线速度为vi , 则 2 定轴转动 刚体绕固定轴z轴转动时, 刚体中任何一点Pi , 都在 垂直于z轴的平面内, 作圆周运动,而且到定轴的距离 相等的点的运动完全一样. 因此研究刚体的定轴转动, 只要研究与转轴垂直的任意平面内的运动即可.其运动 学的独立变量为1. i i v r i Ri v 角量表示: 角位移 角加速度 角速度 ri v R i i mi y x z ω

d a,=(而×)=而x万+Dx可 dt 定轴转动,0方向不变,则 a==Ro=Ra R α是角加速度.在定轴转动中,它的指向与角速 度相同或相反,并且也是沿着同一条转动轴线 速度、加速度的直角坐标系分解请同学们自行给出。 超卓课程《理论力学》
超卓课程《理论力学》 定轴转动, 方向不变, 则 i i i i in i i i i R v R v a a v R R 2 2 是角加速度. 在定轴转动中, 它的指向与角速 度相同或相反, 并且也是沿着同一条转动轴线. v Ri i mi y x z 速度、加速度的直角坐标系分解请同学们自行给出

定轴转动 速度、加速度的直角坐标系分解 T7 k =×=000=-0y,i+0xJ aa=求,=-y,0-02x 4,=y=x,0-02y 42=2,=0 超卓课程《理论力学》
超卓课程《理论力学》 y i x j x y z i j k v r i i i i i i i z 0 0 0 2 2 iz i iy i i i ix i i i a z a y x y a x y x i x i y 定轴转动 速度、加速度的直角坐标系分解

定轴转动 动量矩定理 M,==10=I0 转动动能 外力为保守力时,机械能守恒 1.02+V=E 2 超卓课程《理论力学》
超卓课程《理论力学》 动量矩定理 外力为保守力时,机械能守恒 转动动能 定轴转动

例题1 复摆:m绕过O点的水平轴作微小振动, 试求:运动方程、振动周期。 解:确定正方向 10=-mgl sin0 L。=ml6=ml+m2 L是什么量? mg 1 方程可化为(G+1)9+gl0=0 g 解出0=Asin( gl +r+) 周期 2π -2π +2 t- =2π gl mgl 超卓课程《理论力学》
超卓课程《理论力学》 例题1 复摆:m 绕过O点的水平轴作微小振动, 试求:运动方程、振动周期。 解:确定正方向 方程可化为 令 解出 C y y mg O l 周期 l c是什么量?

2π 周期 +12 T= 2=2π =2π gl mgl 讨论:等价单摆周期 1=21 r= mg 1,-mll=mltml r-1- 以0悬点。=m+m-)=m 2+2 =2π, =2π mg(t'-1) gl mg 1入 测g的原理 超卓课程《理论力学》
超卓课程《理论力学》 周期 讨论:等价单摆周期 以 O' 悬点 测 g 的原理 C y y mg O l O
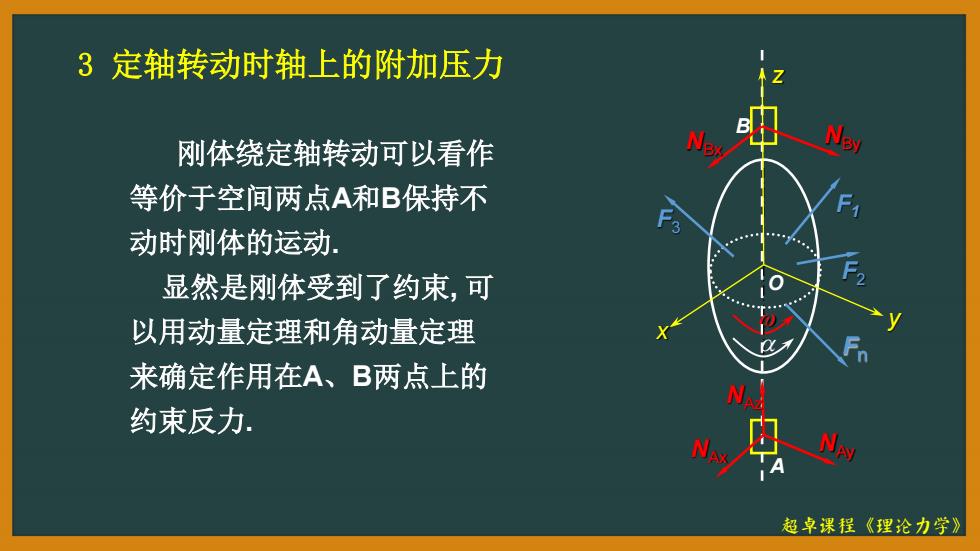
3定轴转动时轴上的附加压力 刚体绕定轴转动可以看作 等价于空间两点A和B保持不 动时刚体的运动 显然是刚体受到了约束,可 以用动量定理和角动量定理 来确定作用在A、B两点上的 A 约束反力 超卓课程《理论力学》
超卓课程《理论力学》 3 定轴转动时轴上的附加压力 刚体绕定轴转动可以看作 等价于空间两点A和B保持不 动时刚体的运动. 显然是刚体受到了约束, 可 以用动量定理和角动量定理 来确定作用在A、B两点上的 约束反力. B A y x z O NBx NBy NAx NAy NAz Fn F1 F2 F3

动量定理 m=N+Na+R d i=l 之my=w+N+2r 对A点的动量矩定理 m0y-)=-丽V+M。 di =1 空-西,空以 正” dt 超卓课程《理论力学》
超卓课程《理论力学》 n i Az iz n i i i n i Ay By iy n i i i n i Ax Bx ix n i i i m z N F t m y N N F t m x N N F t 1 1 1 1 1 1 d d d d d d n i iz n i i i i i i n i Bx iy n i i i i i i n i By ix n i i i i i i m x y y x M t m z x z x AB N M t m y z z y AB N M t 1 1 1 1 1 1 ( ) d d ( ) d d ( ) d d 动量定理 对A点的动量矩定理 A B O F3 Fn F1 F2 x y z Ri NBx NBy NAx NAy NAz