
§5.2虚功原理 导读 ·实位移虚位移 。实功虚功 ·虚功(虚位移)原理 ·拉格朗日乘子与约束力
§5.2 虚功原理 导读 • 实位移 虚位移 • 实功 虚功 • 虚功(虚位移)原理 • 拉格朗日乘子与约束力

1实位移和虚位移 质点由于运动实际发生的位移,叫做实位移.用d表示 想象的质点在约束许可情况下发生的位移,叫做虚位 移.用δ表示.虚位移只决定于质点在此时的位置和加 在它上面的约束,而不是由于时间变化所引起的. 虚位移和实位移的区别是实位移要满足运动方程,而 虚位移只需要满足约束.在稳定约束下,实位移是无限多 虚位移中的一个.而在不稳定约束时,可能二者不一致
1 实位移和虚位移 质点由于运动实际发生的位移, 叫做实位移. 用dr表示. 想象的质点在约束许可情况下发生的位移, 叫做虚位 移. 用 r表示. 虚位移只决定于质点在此时的位置和加 在它上面的约束, 而不是由于时间变化所引起的. 虚位移和实位移的区别是实位移要满足运动方程,而 虚位移只需要满足约束. 在稳定约束下,实位移是无限多 虚位移中的一个. 而在不稳定约束时, 可能二者不一致

设有n个质点的系统,存在m个完整约束,其约束方程 f(G,.,万n,t)=0 (i=1,2,.,m) 设,.,n是满足约束条件的虚位移,则 f(G+,万+2,.,+n,)=0 (i=1,2,.,m) 对6r作多元函数的泰勒展开(t被“冻结”),略去二 次以上的项, ∑7/(G,五,.,i)=0 (j=1,2,.,m) 满足上式的一组r,就是虚位移
设有n个质点的系统, 存在m个完整约束, 其约束方程 ( , , , , ) 0 ( 1,2, , ) f i r1 r2 rn t i m = = 设 r r rn 是满足约束条件的虚位移, 则 1 , 2 , , ( , , , , ) 0 ( 1,2, , ) f i r1 r1 r2 r2 rn rn t i m + + + = = 对 ri 作多元函数的泰勒展开(t 被“冻结”), 略去二 次以上的项, ( , , , , ) 0 ( 1,2, , ) 1 f r1 r2 r t ri j m n i i j n = = = 满足上式的一组ri 就是虚位移

而真实位移dr是一个在时间d间隔中完成的位移, 为使其满足约束条件,必须 f(G+d,+d,.,fn+dn,t+d)=0(i=1,2,.,m 于是得 d+/d=0 (=1,2,.,m) 是约束对真实位移的限制条件,即时间不被“冻结” 的可能位移应满足的条件如约束是稳定的,虚、实位 移相同
而真实位移dri是一个在时间dt间隔中完成的位移, 为使其满足约束条件, 必须 ( d , d , , d , d ) 0 ( 1,2, , ) f i r1 r1 r2 r2 rn rn t t i m + + + + = = 于是得 d / d 0 ( 1,2, , ) 1 f ri f j t t j m n i i j + = = = 是约束对真实位移的限制条件, 即时间不被“冻结” 的可能位移应满足的条件. 如约束是稳定的,虚、实位 移相同
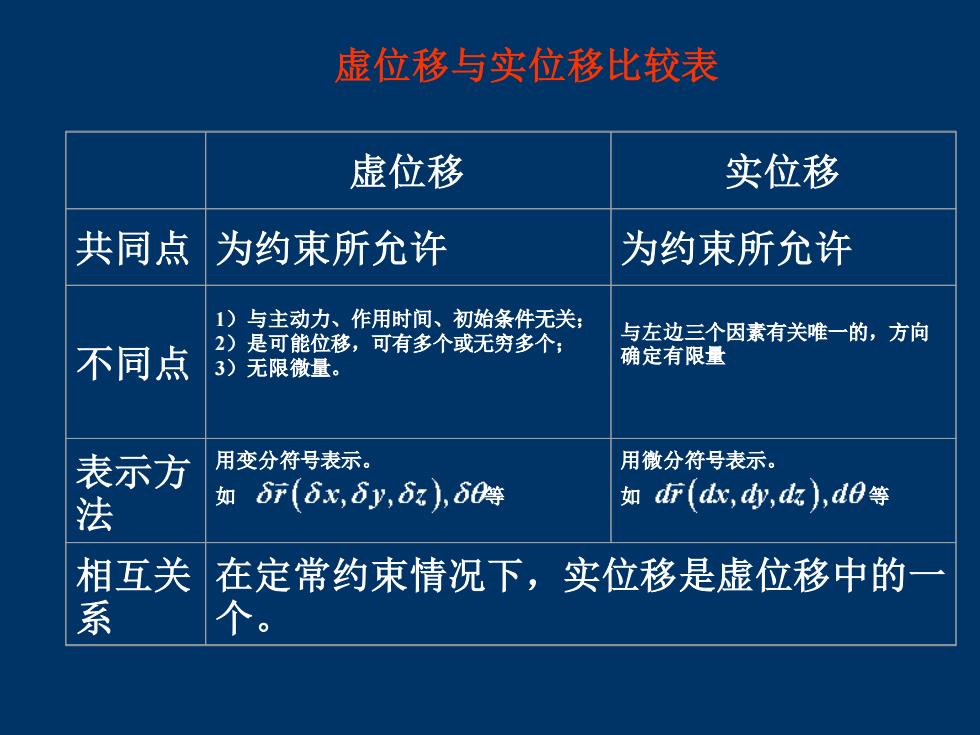
虚位移与实位移比较表 虚位移 实位移 共同点 为约束所允许 为约束所允许 1)与主动力、作用时间、初始条件无关: 不同点 2)是可能位移,可有多个或无穷多个: 与左边三个因素有关唯一的,方向 3)无限微量。 确定有限量 示方 用变分符号表示。 用微分符号表示。 法 如6(6x,6y,6z),60 如标(d,dk),d0等 相互关 在定常约束情况下,实位移是虚位移中的 系 个
虚位移与实位移比较表 虚位移 实位移 共同点 为约束所允许 为约束所允许 不同点 1)与主动力、作用时间、初始条件无关; 2)是可能位移,可有多个或无穷多个; 3)无限微量。 与左边三个因素有关唯一的,方向 确定有限量 表示方 法 用变分符号表示。 如 等 用微分符号表示。 如 等 相互关 系 在定常约束情况下,实位移是虚位移中的一 个

2虚功 作用在质点上的力在任意虚位移δ中所作得功,叫做 虚功 如果作用在一个力学系统上所有作用反力在任意虚 位移中所作得虚功之和为零,即 ∑R心=0 (5.6) 那么系统受到得约束叫做理想约束.一切光滑接触以及 刚体等都是理想约束:
2 虚功 作用在质点上的力在任意虚位移r中所作得功, 叫做 虚功. 如果作用在一个力学系统上所有作用反力在任意虚 位移中所作得虚功之和为零,即 0 (5.6) 1 = = n i i i R r 那么系统受到得约束叫做理想约束. 一切光滑接触以及 刚体等都是理想约束

例1:质点沿固定的光滑曲面运动,约束方程为 f(x,y,2)=0 质点的虚位移应满足 x,yx+(xy2+x,y2&=0 02 即虚位移垂直于曲面的法向( afaf of ).由于约束面 是光滑的,约束力沿曲面的法向,即 R=2 of(x,y,=)of(x,y,=)f(x,y,=)
例1: 质点沿固定的光滑曲面运动, 约束方程为 f (x, y,z) = 0 质点的虚位移应满足 0 ( , , ) ( , , ) ( , , ) = + + z z f x y z y y f x y z x x f x y z = z f x y z y f x y z x f x y z R ( , , ) , ( , , ) , ( , , ) 即虚位移垂直于曲面的法向( ). 由于约束面 是光滑的, 约束力沿曲面的法向, 即 z f y f x f ,

因此虚功为 6M=R.=2 y2+xy+x,y 例2:质点沿运动的光滑曲面运动,约束方程为 f(x,y,2,t)=0 质点的虚位移应满足 过&=0 即虚位移仍垂直于曲面的法向.而约束力沿曲面的法向, 所以虚功也仍为零
因此虚功为 0 ( , , ) ( , , ) ( , , ) = + + = = z z f x y z y y f x y z x x f x y z W R r 例2: 质点沿运动的光滑曲面运动, 约束方程为 f (x, y,z,t) = 0 质点的虚位移应满足 = 0 + + z z f y y f x x f 即虚位移仍垂直于曲面的法向. 而 约束力沿曲面的法向, 所以虚功也仍为零

注意,这里约束力所作的真实的功并不为零,因为真实 位移dr满足 dx+dy+ a对dt=0 它并不垂直于曲面的法向.约束力的虚功为零,这完全 是因为虚位移在“冻结”了的(=0)曲面的切平面上
注意, 这里约束力所作的真实的功并不为零, 因为真实 位移dr满足 d d d d = 0 + + + t t f z z f y y f x x f 它并不垂直于曲面的法向. 约束力的虚功为零, 这完全 是因为虚位移在“冻结”了的(t=0)曲面的切平面上

例3:质点约束在光滑曲线上运动.这种情形可以看成质点 约束在两个光滑曲面上的运动,其约束方程为 f(x,y,2,t)=0 f(x,y,2,t)=0 质点的虚位移应满足 x+ 8x ay &=0 x+ a=0 这也是约束力和虚位移垂直的情况.故虚功为零:
例3:质点约束在光滑曲线上运动. 这种情形可以看成质点 约束在两个光滑曲面上的运动, 其约束方程为 = = ( , , , ) 0 ( , , , ) 0 2 1 f x y z t f x y z t 质点的虚位移应满足 = + + = + + 0 0 2 2 2 1 1 1 z z f y y f x x f z z f y y f x x f 这也是约束力和虚位移垂直的情况. 故虚功为零