
第4章弯曲内力
第4章 弯曲内力

>☒§4-1弯曲的概念和实例 >☑§4-2受弯构件的简化 D §4-3剪力和弯矩 > §4-4剪力方程和弯矩方程剪力图和弯矩图 ☒ §4-5载荷集度、剪力和弯矩间的关系 心☑§4-6平面曲杆的弯曲内力
§4-1 弯曲的概念和实例 §4-2 受弯构件的简化 §4-3 剪力和弯矩 §4-4 剪力方程和弯矩方程 剪力图和弯矩图 §4-5 载荷集度、剪力和弯矩间的关系 §4-6 平面曲杆的弯曲内力
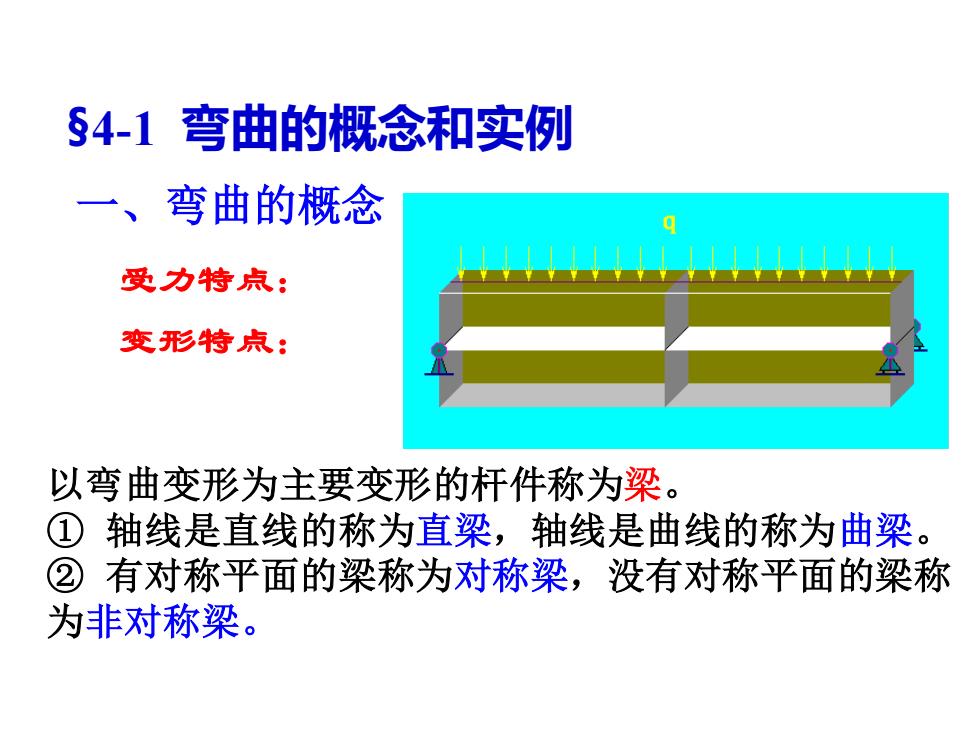
§4-1弯曲的概念和实例 一、弯曲的概念 受力特点: 变形特点: 以弯曲变形为主要变形的杆件称为梁。 ①轴线是直线的称为直梁,轴线是曲线的称为曲梁。 ②有对称平面的梁称为对称梁,没有对称平面的梁称 为非对称梁
§4-1 弯曲的概念和实例 受力特点: 变形特点: 一、弯曲的概念 以弯曲变形为主要变形的杆件称为梁。 ① 轴线是直线的称为直梁,轴线是曲线的称为曲梁。 ② 有对称平面的梁称为对称梁,没有对称平面的梁称 为非对称梁

对称弯曲:若梁上所有外力都作用在纵向对称面内,梁变形 后轴线形成的曲线也在该平面内的弯曲。 纵向对称面 非对称弯曲:若梁不具有纵向对称面,或梁有纵向对称面上 但外力并不作用在纵向对称面内的弯曲。 对称弯曲时和特定条件下的非对称弯曲时,梁的挠曲线与 外力所在平面相重合,这种弯曲称为平面弯曲
对称弯曲:若梁上所有外力都作用在纵向对称面内,梁变形 后轴线形成的曲线也在该平面内的弯曲。 非对称弯曲:若梁不具有纵向对称面,或梁有纵向对称面上 但外力并不作用在纵向对称面内的弯曲。 F q FA FB 纵向对称面 对称弯曲时和特定条件下的非对称弯曲时,梁的挠曲线与 外力所在平面相重合,这种弯曲称为平面弯曲
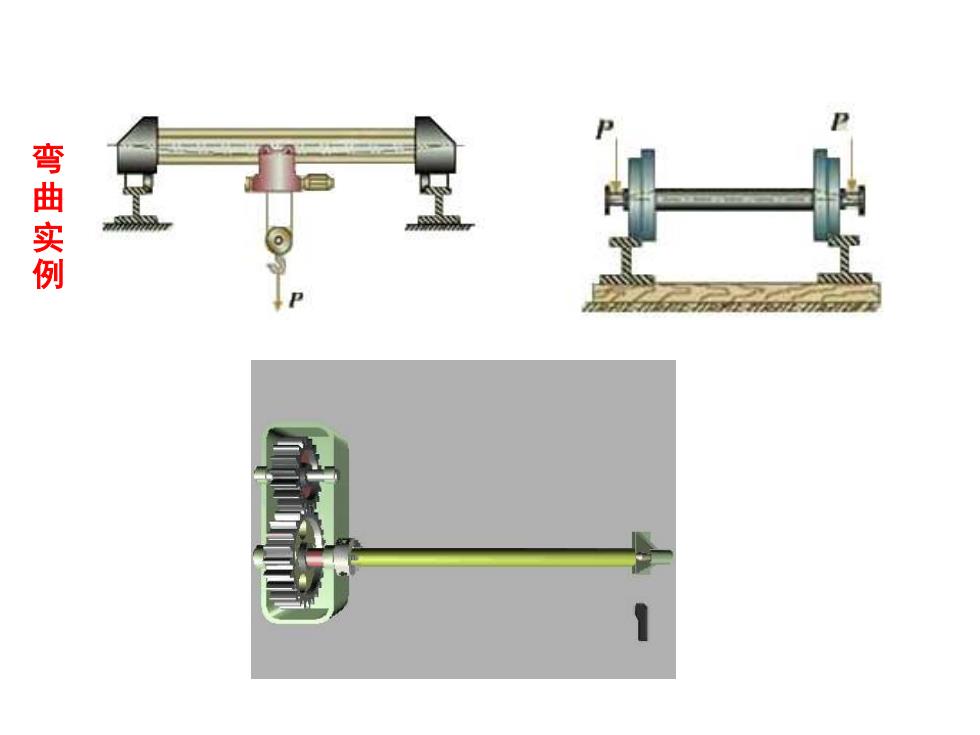
弯曲实例
弯曲实例
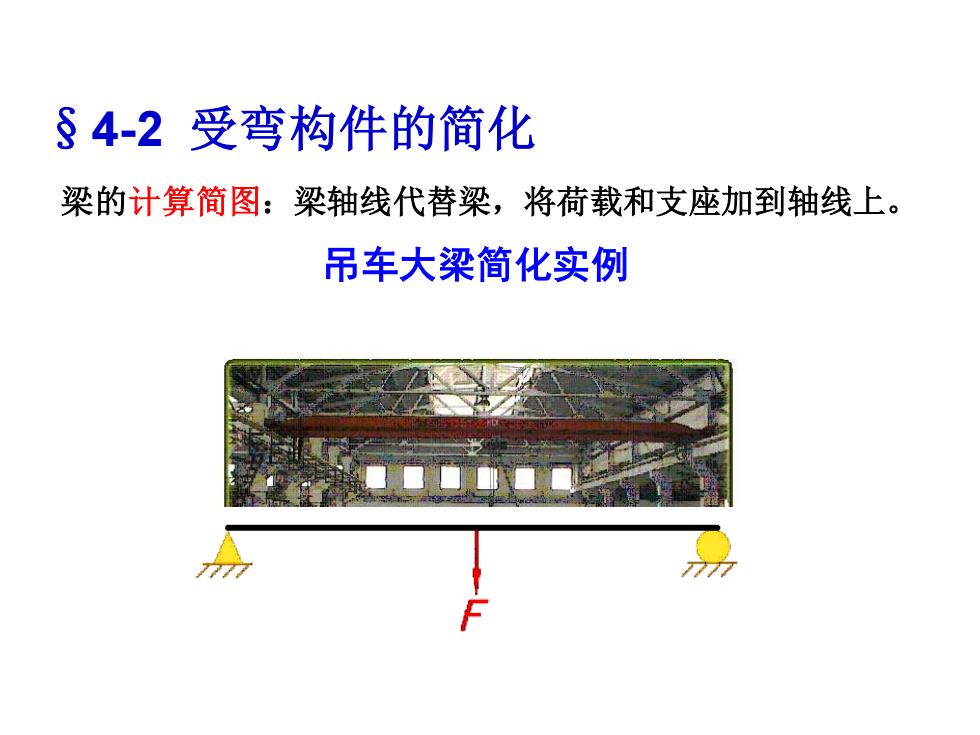
§4-2受弯构件的简化 梁的计算简图:梁轴线代替梁,将荷载和支座加到轴线上。 吊车大梁简化实例 77
§4-2 受弯构件的简化 梁的计算简图:梁轴线代替梁,将荷载和支座加到轴线上。 吊车大梁简化实例
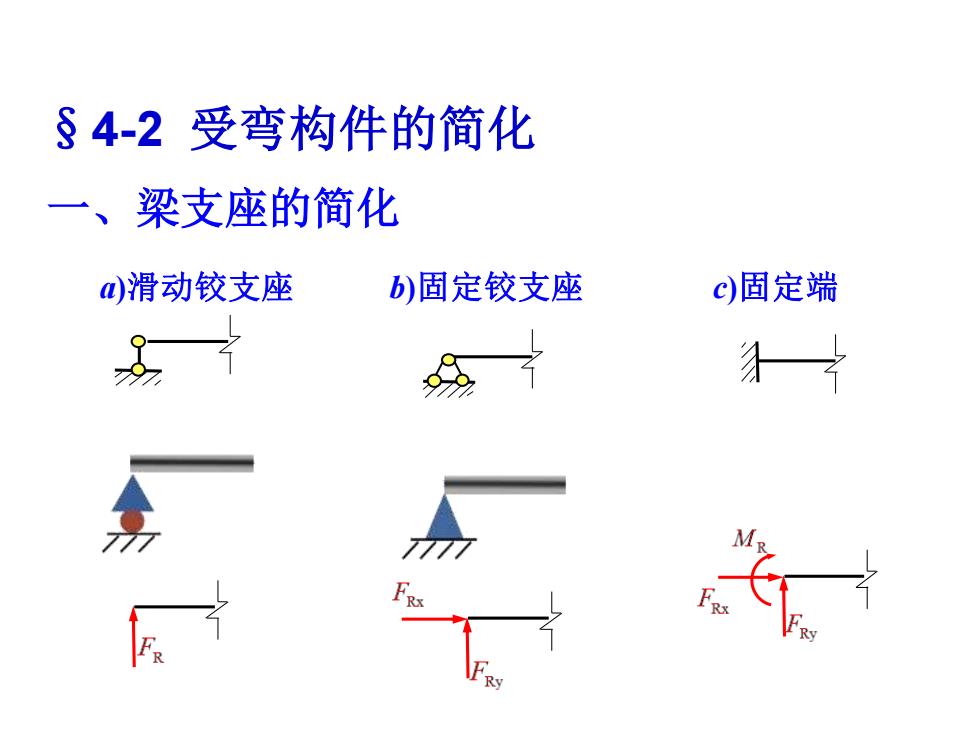
§4-2受弯构件的简化 一、梁支座的简化 滑动铰支座 b)固定铰支座 c)固定端 牙片
§4-2 受弯构件的简化 一、梁支座的简化 a)滑动铰支座 b)固定铰支座 c)固定端
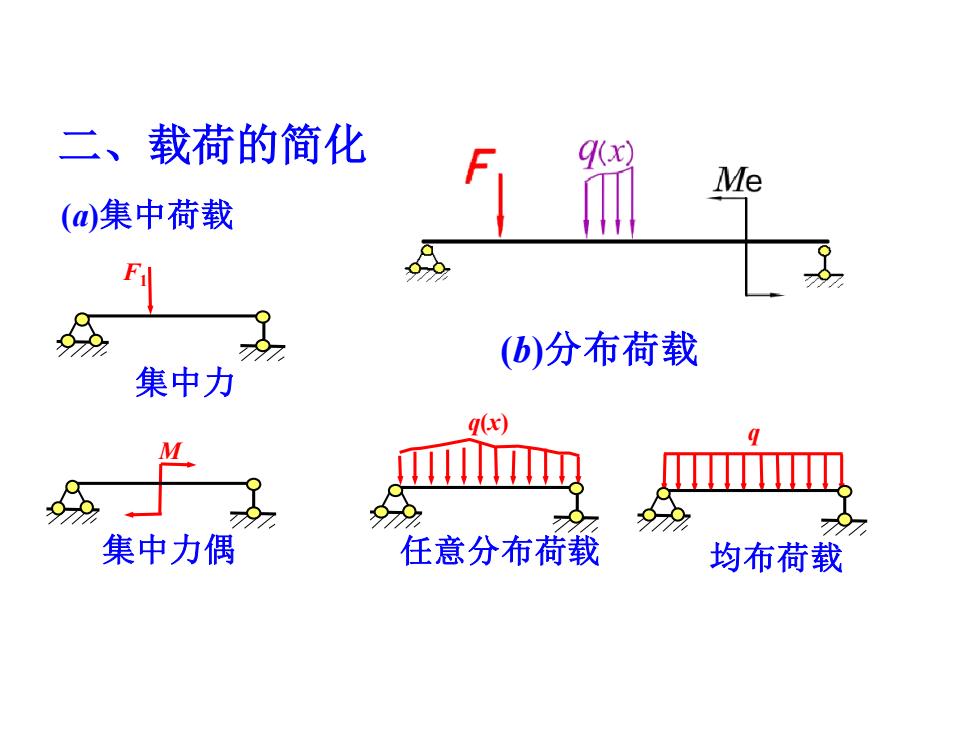
二、载荷的简化 Me (a)集中荷载 F 9 (b)分布荷载 集中力 q(x) M 集中力偶 任意分布荷载 均布荷载
二、载荷的简化 (a)集中荷载 F1 集中力 M 集中力偶 (b)分布荷载 q(x) 任意分布荷载 q 均布荷载
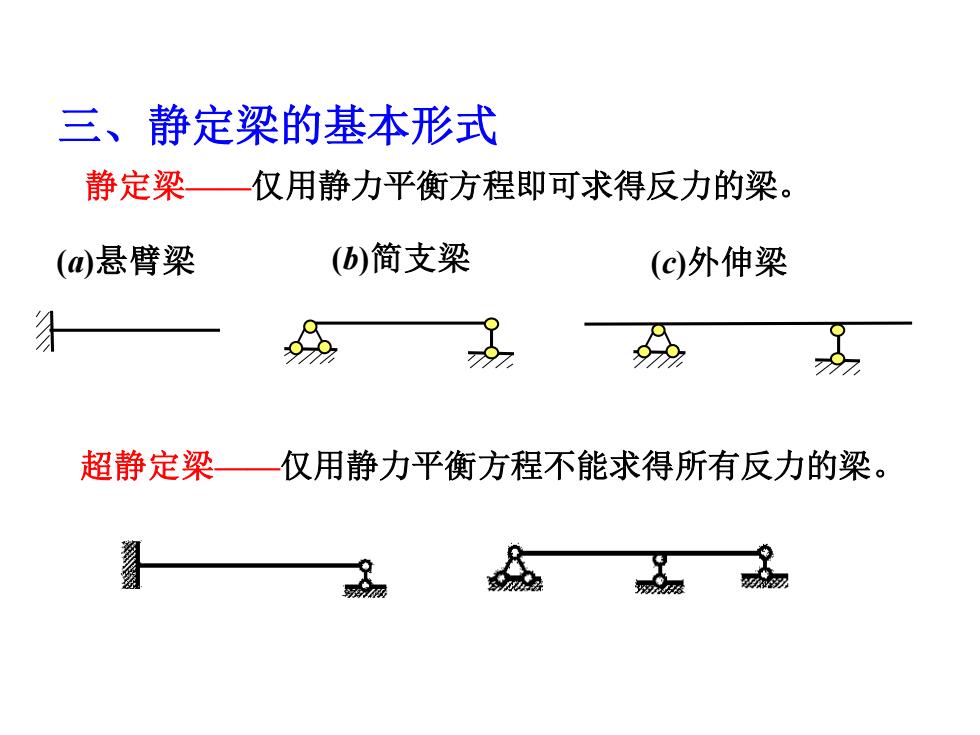
三、静定梁的基本形式 静定梁 仅用静力平衡方程即可求得反力的梁。 (a)悬臂梁 (b)简支梁 (c)外伸梁 超静定梁一仅用静力平衡方程不能求得所有反力的梁
静定梁——仅用静力平衡方程即可求得反力的梁。 (a)悬臂梁 (b)简支梁 (c)外伸梁 三、静定梁的基本形式 超静定梁——仅用静力平衡方程不能求得所有反力的梁

§4-3剪力和弯矩 a FB=1 ∑F=0:Fa-F=0→F=F ∑Mc=0:M-FAx=0→M=Fx 剪力 矩 E∑F=0:F+F-F=0→F=F-F=F ∑M=0:M+F[l-x-(I-a]-F(I-x)=0→M=Fax
§4-3 剪力和弯矩 y A S 0 S A F = 0: F − F = F = F M M F x M F x C A 0 A = 0: − = = x C F C y S B 0 S B A F = 0: F + F − F = F = F − F = F M M F l x l a F l x M F x C A = + − − − − − = = 0: [ ( )] 0 B ( ) F l l a FA − = F l a FB =