理论力学复习题 一、判断题:正确的划√,错误的划× 1.力的可传性适用于刚体和变形体。 2.平面上一个力和一个力偶可以简化成一个力。 3.在刚体运动过程中,若其上有一条直线始终平行于它的初始位置,这种刚体 的运动就是平动。 ( 4.两相同的均质圆轮绕质心轴转动,角速度大的动量矩也大。 ( 5.质点系的动量为零,其动能也必为零。 6.刚体上只作用三个力,且它们的作用线汇交于一点,该刚体必处于平衡状态。 7.如图只要力F处于摩擦角之内,物体就静止不动。 ( i11521111 8.各点都作圆周运动的刚体一定是定轴转动。 9.两相同的均质圆轮绕质心轴转动,角速度大的动量也大。 10·质点系的内力不能改变质点系的动量和动量矩。 ( 二、选择题: 1.将图a所示的力偶m移至图b的位置,则()。 A.A、B、C处约束反力都不变 B.A处反力改变,B、C处反力 不变 C.A,C处反力不变,B处反力改变 D.A,B、C处约束反力都要改 变 2.图示一平衡的空间平行力系,各力作用线与z轴平行,如下的哪些组方程 可作为该力系的平衡方程组()
理论力学复习题 一、判断题:正确的划√,错误的划× 1.力的可传性适用于刚体和变形体。 ( ) 2.平面上一个力和一个力偶可以简化成一个力。 ( ) 3.在刚体运动过程中,若其上有一条直线始终平行于它的初始位置,这种刚体 的运动就是平动。 ( ) 4.两相同的均质圆轮绕质心轴转动,角速度大的动量矩也大。 ( ) 5.质点系的动量为零,其动能也必为零。 ( ) 6.刚体上只作用三个力,且它们的作用线汇交于一点,该刚体必处于平衡状态。 ( ) 7.如图只要力 F 处于摩擦角之内,物体就静止不动。 ( ) 8.各点都作圆周运动的刚体一定是定轴转动。 ( ) 9.两相同的均质圆轮绕质心轴转动,角速度大的动量也大。 ( ) 10 . 质 点 系 的 内 力 不 能 改 变 质 点 系 的 动 量 和 动 量 矩 。 ( ) 二、选择题: 1.将图 a 所示的力偶 m 移至图 b 的位置,则( )。 A. A、B、C 处约束反力都不变 B . A 处反力改变,B、C 处反力 不变 C. A 、C 处反力不变, B 处反力改变 D . A、B、C 处约束反力都要改 变 m m a b A B C A C B 2.图示一平衡的空间平行力系,各力作用线与 z 轴平行,如下的哪些组方程 可作为该力系的平衡方程组( )。 F G

∑X=0 ∑X=0 AY=0 BY=0 ∑M,=0 ∑M.=0 ∑Z=0 ∑M.=0 ∑M,=0 D∑M,=0 ∑M,=0 ∑M,=0 3.如图所示,质量为m,长为L的匀质杆OA,以匀角速度ω绕O轴转动,图 示位置时,杆的动量、对O轴的动量矩的大小分别为( 。 A.p=1/2mLo Lo =mLo/12 B.p=0 Lo =mLo/12 C.p=1/2mLo D.p=1/2mL@ Lo=mLo/3 4.点M沿半径为R的圆周运动,其速度和,k 是有量纲的常数。则点M 的全加速度为( A.k'R+ B'P/R2+k C.kP/R+k2 k2/R2+k2 5.动点沿其轨迹运动时( A.若a三0,an≠0,则点作变速曲线运动 B.若a,=0,an≠0,则点作匀速率曲线运动 C.若a,≠0,an■0,则点作变速曲线运动 D.若a,≠0,an=0,则点作匀速率曲线运动 6.一刚体上只有两个力偶M、M作用,且M+M=0,则此刚体( A.一定平衡B.一定不平衡C.平衡与否不能判定D.平衡与否与力偶作用位 置有关 7.图示四个力偶中,()是等效的
3.如图所示,质量为 m,长为 L 的匀质杆 OA,以匀角速度ω绕 O 轴转动,图 示位置时,杆的动量、对 O 轴的动量矩的大小分别为( )。 A. 1/ 2 /12 2 p = mL LO = mL B. 0 /12 2 p = LO = mL C. p mL LO mL )L 2 1 ( 2 1 = 1/ 2 = D. 1/ 2 / 3 2 p = mL LO = mL 4.点 M 沿半径为 R 的圆周运动,其速度为 是有量纲的常数。则点 M 的全加速度为( )。 A. B. C. D. 5. 动点沿其轨迹运动时( )。 A.若 a 0, an 0 ,则点作变速曲线运动 B.若 a 0, an 0 ,则点作匀速率曲线运动 C.若 a 0, an 0 ,则点作变速曲线运动 D.若 a 0, an 0 ,则点作匀速率曲线运动 6.一刚体上只有两个力偶 MA、MB作用,且 MA + MB = 0,则此刚体( )。 A.一定平衡 B.一定不平衡 C.平衡与否不能判定 D.平衡与否与力偶作用位 置有关 7.图示四个力偶中,( )是等效的。 得分 评卷人 z o y F1 F2 Fn x F3 = = = = = = = = = = = = 0 0 0 . 0 0 0 . 0 0 0 . 0 0 0 . z y x y x x z M M M D M M Z C M Y X B M Y X A 2 2 2 k t R + k 2 2 2 2 k t R + k 4 4 2 2 k t R + k 4 2 2 2 k t R + k v = kt,k

181 6d 间 A.(a)与b)与(c) B.b)与(c) C.(c)与(d) D.(a)与b)与d) 8.图示平行四连杆机构O1ABO2,ABC为一刚性三角形板,则C点的切向加速 度为:( A.a=AO1 a C B.a,=ACa A C.a,=COI D.a:=BCa 9.圆盘以匀角速度ω绕定轴O转动,动点M相对圆盘以匀速r沿圆盘直径 运动,如题图所示。当动点M到达圆盘中心O位置时,如下哪组给出的科氏加 速度ac是正确的?( ) A.a=0 B.a=-2o,方向垂直向上 C.a=2w,方向垂直向下 D.k=un,方向垂直向上 10.图示P点沿螺线自外向内运动,它走过的弧长与时间的一次方成正比,关于 该点的运动,有以下4种答案,请判断哪一个答案是正确的:( A.速度越来越快 B.速度越来越慢 C.加速度越来越大D.加速度越来越小 三、填空题: 1.图示结构,各构件自重不计,ABC杆水平,M=6kN·m,a=lm,则A处约束 力的大小为 kN,方向为
A. (a)与(b)与(c) B. (b) 与(c) C. (c)与(d) D. (a)与(b)与(d) 8.图示平行四连杆机构 O1ABO2,ABC 为一刚性三角形板,则 C 点的切向加速 度为: ( )。 9.圆盘以匀角速度ω绕定轴 O 转动,动点 M 相对圆盘以匀速 vr 沿圆盘直径 运动,如题图所示。当动点 M 到达圆盘中心 O 位置时,如下哪组给出的科氏加 速度 ac 是正确的? ( ) 10.图示 P 点沿螺线自外向内运动,它走过的弧长与时间的一次方成正比,关于 该点的运动,有以下 4 种答案,请判断哪一个答案是正确的:( ) A. 速度越来越快 B. 速度越来越慢 C. 加速度越来越大 D. 加速度越来越小 三、填空题: 1.图示结构,各构件自重不计,ABC 杆水平,M=6kN·m,a=1m,则 A 处约束 力的大小为 kN,方向为 。 A B C O O2 1 α ω O M r v 上 左 右 下 P A. aτ= AO1α B. aτ= ACα C. aτ= CO1α D. aτ= BCα A.ac=0 B.ac=2ωvr, 方向垂直向上 C.ac =2ωvr, 方向垂直向下 D.ac =ωvr, 方向垂直向上
2.作用在刚体上的力是滑移矢量,力偶矩是 矢量,力对点的矩是定位 矢量。 3.均质圆轮质量为m,半径为,绕0转动如图,其动量为 ,对0 点的动量矩 4.质量为m、半径为R的均质轮子沿轨道以角速度ω纯滚动,该轮子的动能 为 5.图中桁架杆1的内力为」 杆2的内力为 杆3的内力 为 2T3 人 5×3m 6.作用在刚体上的力是滑移矢量,力偶矩是自由矢量,力对点的矩是矢量。 7.设车厢上水平向右的牵引力F为常力,大小为F=10KN,作用时间△M=1Os 则这段时间内,力F的冲量I的大小为」 _,冲量I的方向 777 8.一给定平衡系统,若所能列出的独立的平衡方程的个数少于所求未知力的个 数,则该问题属于 问题。 9.如图所示简支梁桁架,已知力F,长度a,则杆1的内力为_ 一,杆 2的内力为 ,杆3的内力为
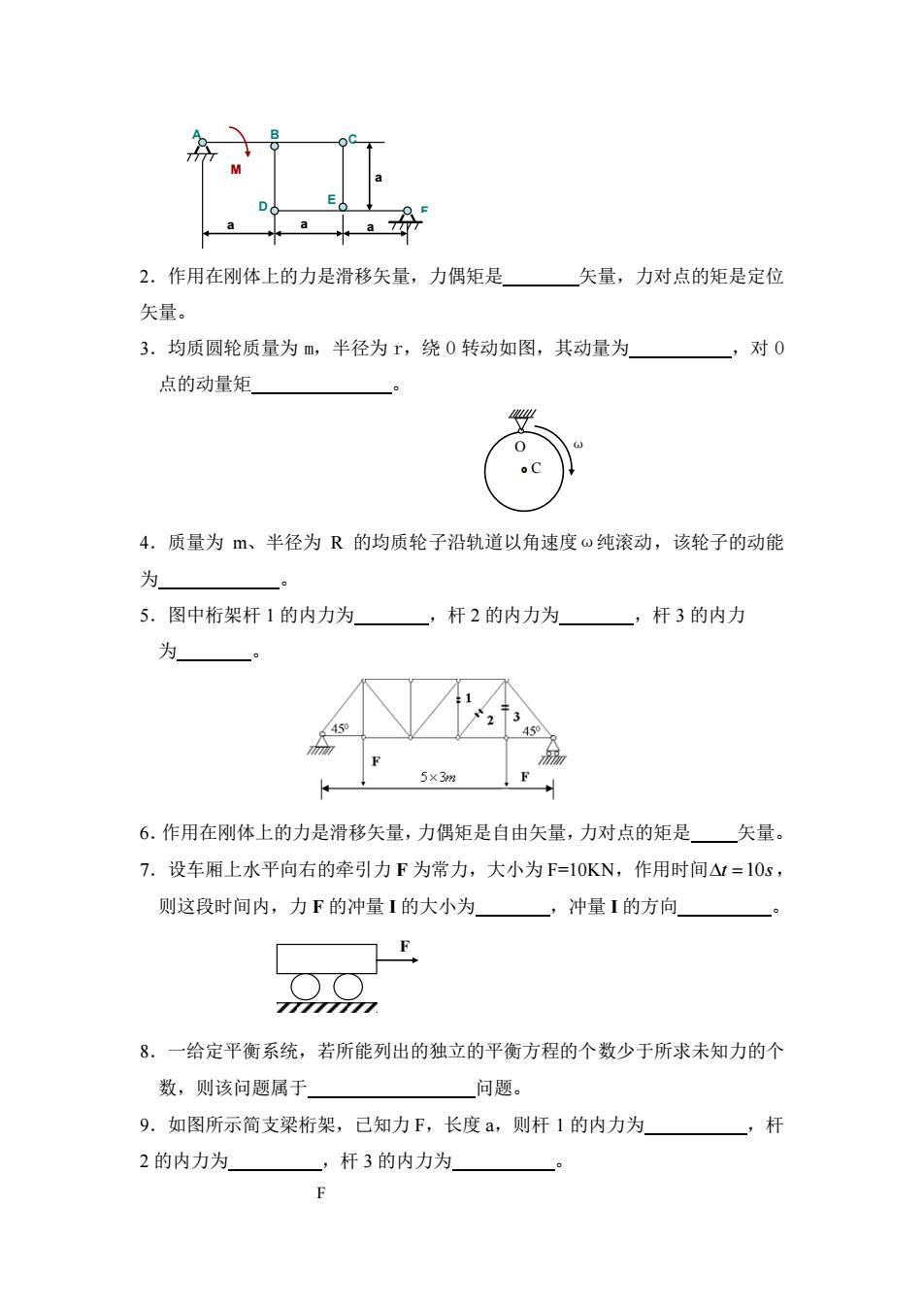
2.作用在刚体上的力是滑移矢量,力偶矩是 矢量,力对点的矩是定位 矢量。 3.均质圆轮质量为 m,半径为 r,绕 O 转动如图,其动量为 ,对 O 点的动量矩 。 4.质量为 m、半径为 R 的均质轮子沿轨道以角速度ω纯滚动,该轮子的动能 为 。 5.图中桁架杆 1 的内力为 ,杆 2 的内力为 ,杆 3 的内力 为 。 6.作用在刚体上的力是滑移矢量,力偶矩是自由矢量,力对点的矩是 矢量。 7.设车厢上水平向右的牵引力 F 为常力,大小为 F=10KN,作用时间 t =10s, 则这段时间内,力 F 的冲量 I 的大小为 ,冲量 I 的方向 。 8.一给定平衡系统,若所能列出的独立的平衡方程的个数少于所求未知力的个 数,则该问题属于 问题。 9.如图所示简支梁桁架,已知力 F,长度 a,则杆 1 的内力为 ,杆 2 的内力为 ,杆 3 的内力为 。 A B C D E F a a a M a ω C O F F
四、简答题: 1.不计各构件的自重,画出杆AB、CD的受力图。(5分) 2.重为G的物块,放在粗糙的水平面上,己知:物块与水平面的摩擦角中=20°, 现受斜侧推力F作用,如图示,若F=G,且F与法线间的夹角度ā=30°,问 该物块是否平衡?(说明原因)(4分) 3.图示各平面机构:(7分) (1)找出各平面运动刚体在图示位置的速度瞬心。 (2)指出各平面运动刚体角速度的转向。 (3)在图中画出M点的速度方向
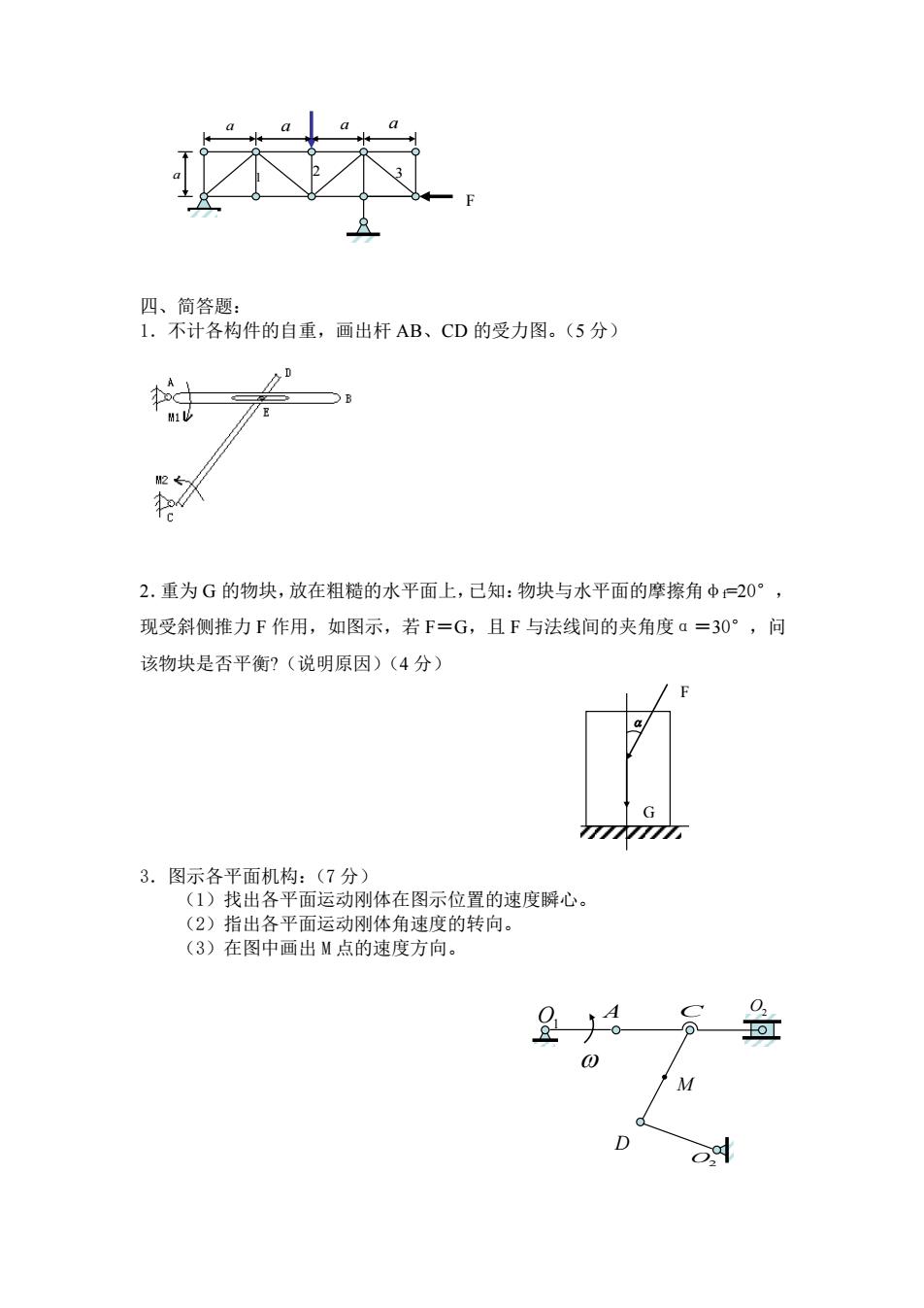
四、简答题: 1.不计各构件的自重,画出杆 AB、CD 的受力图。(5 分) 2.重为 G 的物块,放在粗糙的水平面上,已知:物块与水平面的摩擦角φf=20°, 现受斜侧推力 F 作用,如图示,若 F=G,且 F 与法线间的夹角度α=30°,问 该物块是否平衡?(说明原因)(4 分) 3.图示各平面机构:(7 分) (1)找出各平面运动刚体在图示位置的速度瞬心。 (2)指出各平面运动刚体角速度的转向。 (3)在图中画出 M 点的速度方向。 O2 M O1 A C D O2 a a a a a 1 2 3 F Q P F G

4.画出图示结构中各构件的受力图。不计各构件重力,所有约束处均为光滑约 束。(5分) 5.(7分)图示平面机构: (1)找出各平面运动刚体在图示位置的速度瞬心。 (2)指出各乎 面运动刚体角速度的转向 (3)在图中画出M点的速度方向。 0 M 五、计算题: 1.直杆AB长=200mm,在铅垂面内运动,杆的两端分别沿铅直墙及水平面滑动, 已知在某瞬时, 60 V=20mm/s(↓)。求此瞬时杆AB的角速度及 A端的速度V及杆AB的中点D的速度。 LB A
4.画出图示结构中各构件的受力图。不计各构件重力,所有约束处均为光滑约 束。(5 分) 5.(7 分)图示平面机构: (1)找出各平面运动刚体在图示位置的速度瞬心。 (2)指出各平面运动刚体角速度的转向。 (3)在图中画出 M 点的速度方向。 五、计算题: 1.直杆 AB 长 L=200mm,在铅垂面内运动,杆的两端分别沿铅直墙及水平面滑动, 如图示,已知在某瞬时,α=60°,VB=20mm/s(↓)。求此瞬时杆 AB 的角速度及 A 端的速度 VA及杆 AB 的中点 D 的速度。 O A B M C O1 F

2.如图,均质杆AD重P,与长为21的铅直杆BE的中点D铰接,绳的下端吊有重 为G的物体M。假设杆BE、滑轮和绳的重量不计,连线AB以及绳的CH段都处于 水平位置:求固定铰链支座A的约束力 e M 3.滚子A,重Q,沿倾角为a的斜面滚动而不滑动,滑轮B与滚子A有相同的 质量和半径,且均可看作均质圆盘,物体C重P,求滚子中心的加速度,设绳 子不可伸长,其重量可略而不计,绳与滑轮间无滑动。 4.两个鼓轮固连在一起,其总质量是m,对水平转轴O的转动惯量是。:鼓 轮的半径是n和B。绳端悬挂的重物A和B质量分别是m和应 (图a),且m>。试求鼓轮的角加速度。 m
2.如图,均质杆 AD 重 P,与长为 2l 的铅直杆 BE 的中点 D 铰接,绳的下端吊有重 为 G 的物体 M。假设杆 BE、滑轮和绳的重量不计,连线 AB 以及绳的 CH 段都处于 水平位置;求固定铰链支座 A 的约束力。 3.滚子 A,重 Q,沿倾角为α的斜面滚动而不滑动,滑轮 B 与滚子 A 有相同的 质量和半径,且均可看作均质圆盘,物体 C 重 P,求滚子中心的加速度,设绳 子不可伸长,其重量可略而不计,绳与滑轮间无滑动。 4.两个鼓轮固连在一起,其总质量是 m,对水平转轴 O 的转动惯量是 JO ;鼓 轮的半径是 r1 和 r2 。绳端悬挂的重物 A 和 B 质量分别是 m1 和 m2 (图 a),且 m1 > m2。试求鼓轮的角加速度。 A B C P Q Q

参考答案 三、填空题: 1.2:垂直向下(竖直向下) 2.自由 3.mro.mro 4.mRo 5.0:0:F6.定位: 7.100KN.s:与力F相同 8.超静定;9.0、-F、0 四、简答题: 1. 一 2 解:此题虽然F与法线夹角x>p, 但F与G的合力FR与法线夹角为150 15°<91分)平衡1分) 3
参考答案 三、填空题: 1.2;垂直向下(竖直向下) 2.自由 3. 2 2 3 mr , mr 4. 2 2 4 3 mR 5.0;0; F 6.定位; 7.100KN.s;与力 F 相同 8.超静定; 9.0、-F、0 四、简答题: 1. 2. 解:此题虽然 F 与法线夹角 f 但 F 与 G 的合力 FR与法线夹角为 150 一、 15 (1 ) (1 ) 0 f 分 平衡 分 3. B M O1 A C D O2 VA VB VC VD VM ω2 ω1
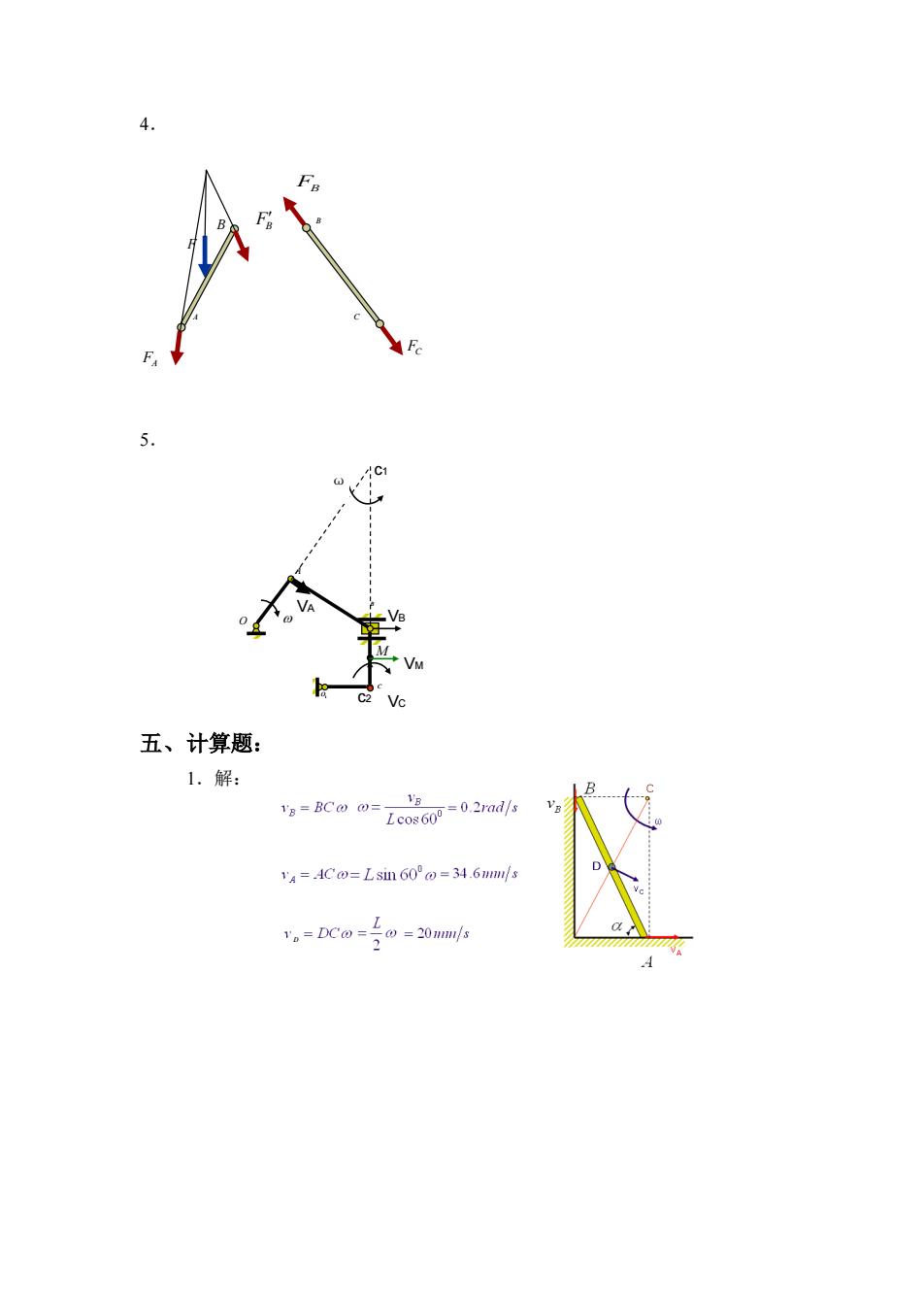
五、计算题: 1.解: V=AC@=Lsin 60@=34.6mmf v。=bcw=子o=20ma
4. 5. 五、计算题: 1.解: O A B M C O1 VA VB c1 VC ω c2 F B A C B FB FA FB FC VM D

2.解:取整体为研究对象。画受力图 F >MB(F)=0 -AB.NAy+AB.P-BE.G=0 取杆AD为研究对象。画受力图 A艾30 ∑Mn=0AD-cos305-N)-AD-sn30PNA=0 w台c:”含@ N=兮-Nwo30=2G Fax =3/2F cot0-ko cot0 3.解: 方法一:达朗贝尔原理 ∑Mg=Qr:sina-G,-Ma4-M-(P+Qe)r=0(4分) 0vmu-g0-号g号8号-e学0 8 22+m=0rsma=Pr(3分) a=80s0a-P(3分) 20+P 方法二:动能定理
2. 解:取整体为研究对象。画受力图 MB(F) = 0 0 2 1 − AB NAy + AB P − BEG = 取杆 AD 为研究对象。画受力图 MD(F) = 0 ) sin 30 0 2 cos30 ( − − Ax = o Ay o N AD N P AD 6 3 4 3 3 2 2 P G G P NAy − = − = N G P N o Ax Ay ) cot30 2 3 2 2 = ( − = FBX = 3/ 2F cot − k 0 cot 3.解: 方法一:达朗贝尔原理 (3 ) 2 ( sin ) ) sin Pr (3 ) 2 ( ( ) 0 (5 ) 2 1 2 1 sin sin ( ) 0 (4 ) 2 2 分 分 分 分 Q P g Q P a ra Qr g P g Q r g pa P r a r g Q r a r g Q r a g Q Q r M Q r rG M M P Q r Bi A G A G B C + − = + = = − − − − + = = − − − − + = 方法二:动能定理