同济大学：《理论力学》课程教学课件（PPT讲稿）第五章 分析力学 5.5 哈密顿正则方程

第五章 分析力学

第五章 分析力学

§5.5哈密顿正则方程 导读 ·勒让德变换 ·正则变量相空间相点 ·哈密顿正则方程 。守恒定理

导读 • 勒让德变换 • 正则变量 相空间 相点 • 哈密顿正则方程 • 守恒定理 §5.5 哈密顿正则方程

1勒让德（勒襄特）变换 在方程中，把一组独立自变量变为另一组独立自变 量的变换，叫勒让德变换。 定义L=1(,痕=九(&，8，i,t 则由拉氏证9x O9a 如果把广义动量和广义坐标作为独立变量，则 9a=9a（P1,p2,.,p,91,92,.,9,t) 从而拉氏量L也可以表示为广义动量和广义坐标的函数 Z=(p1,P2,P,91,92,.,9,）

1 勒让德（勒襄特）变换 在方程中, 把一组独立自变量变为另一组独立自变 量的变换, 叫勒让德变换. 定义广义动量    q T q L p     =   = 则由拉氏方程, 得   q L p    = 如果把广义动量和广义坐标作为独立变量, 则 ( , , , , , , , , ) 1 2 1 2 q q p p p q q q t  s  s    =  从而拉氏量L也可以表示为广义动量和广义坐标的函数 ( , , , , , , , , ) 1 2 1 2 L L p p p q q q t =  s  s

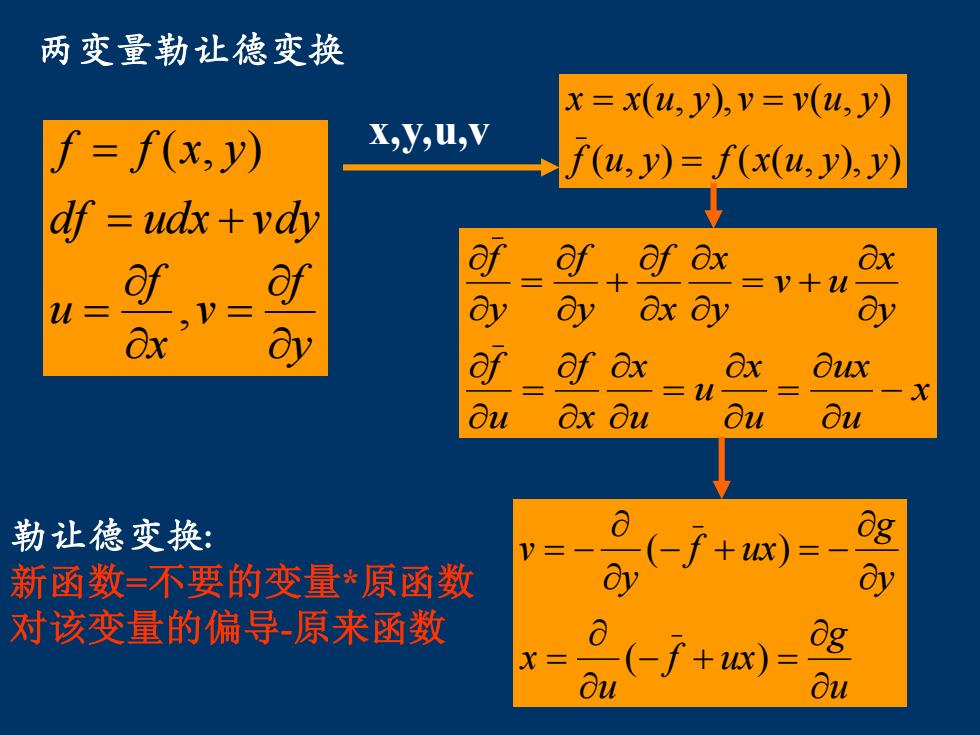
两变量勒让德变换 x=x(u,y),v=v(u,y) ∫=f(x,y) x,y,U,V f(u,y)=f(x(u,y),y) df udx vdy af 可_af+fx ay ax ay =v+u 8x W= ay 8x of of ax Ox Oux 三u Ou Ox Ou ou Ou 勒让德变换： （-f+)=- g 新函数=不要的变量*原函数 y 对该变量的偏导原来函数 (-f+1)= X三 ou Bu

两变量勒让德变换 y f v x f u   =   = , x,y,u,v ( , ) ( ( , ), ) ( , ), ( , ) f u y f x u y y x x u y v v u y = = = df udx vdy f f x y = + = ( , ) x u ux u x u u x x f u f y x v u y x x f y f y f −   =   =     =     = +     +   =   u g f ux u x y g f ux y v   − + =   =   − + = −   = − ( ) 勒让德变换 ( ) : 新函数=不要的变量*原函数 对该变量的偏导-原来函数

2正则方程 当认为L是广义坐标，广义速度和时间的函数时 aL aL 考虑广义动量的定义，得 -2以+g.)广 对于哈密顿量 H(p,90=-L+∑P9。 可得 aH=-d++9-+p.)

当认为L是广义坐标, 广义速度和时间的函数时 t t L q q L q q L L s d d d d 1   +          +   =   =       考虑广义动量的定义, 得 2 正则方程 ( ) t t L L p q p q s d d d d 1   =  + +  =       对于哈密顿量 = = − + s H p q t L p q 1 ( , , )     可得 ( ) ( ) t t L H L p q q p p q q p s s d d d d d d d 1 1   = − +  + =  − + − =  =             

H作为广义动量，广义坐标和时间的函数，又有 dH 09. pa 由于动量，坐标和时间都是独立的，所以 OH qa= Opa (C=1,2,.,s) aH Pa=- dqa 哈密顿正则方程 相应的广义动量，坐标叫做正则变量，它们组成的2s维 空间叫相空间，一组数值对应相空间中一点，叫相点：

H作为广义动量, 广义坐标和时间的函数,又有 t t H p p H q q H H s d d d d 1   +          +   =   =     由于动量, 坐标和时间都是独立的,所以 ( 1,2, ,s) q H p p H q    =          = −   =      ——哈密顿正则方程 相应的广义动量, 坐标叫做正则变量, 它们组成的2s维 空间叫相空间, 一组数值对应相空间中一点,叫相点

维弹簧振子的运动 L=T-V P,= 哈密顿量 a4: H=Eg+E=mx2/2+kx2/2 p.广义动量 x.广义位移 哈密顿正则方程： 2m OH p x= 动量定义 OH 牛顿第二定律 Ox m=-kx 即：mx+kx=0

• 哈密顿量 2 2 2 2 2 1 2 / 2 / 2 k x m p H E E mx k x k p = + = + =  + 动量定义 牛顿第二定律 p .广义动量 x.广义位移 m x  = − k x 即： m x  + k x = 0 m p p H x =    = k x x H p = −    = − 哈密顿正则方程： 一维弹簧振子的运动 i i q L p    L = T − V =

3守恒定理 (1)能量守恒 因为 dH aH OH dt qa Opa Ot aH OH OHOH aH OH Ot Ot 只要不显含时间，它就是守恒的，即不随时间变化

因为 3 守恒定理 t H t H q H p H p H q H t H p p H q q H t H s s   =   +            −     =   +          +   =   = = 1 d 1 d             只要H不显含时间, 它就是守恒的, 即不随时间变化. （1） 能量守恒

H中不显含时，再分稳定约束与不稳定约束这两种情 况来讨论。 )稳定约束 T=T 22既}n H=-L+之g=-(T-八+27 Q= H=T+V=h=const 对于完整的保守力学体系来说，若不显含t,而且 体系受稳定约束时，体系的是能量积分，这时体系的 机械能守恒

H中不显含t时，再分稳定约束与不稳定约束这两种情 况来讨论。 i）稳定约束 T＝T2 q T q T q q T s s 2 1 2 1 =           =             =  =          =   = − + s q q T H L  1     = −(T − V ) + 2T H = T ＋ V = h = const 对于完整的保守力学体系来说，若H不显含t，而且 体系受稳定约束时，体系的H是能量积分，这时体系的 机械能守恒

i)不稳定约束 T =T+T+To 9。=27+7 @-1 以 of-du=T2-To+V H=T2-To V=h=const 可见，对于完整的保守力学体系来说，若H中不 显含t,而且体系受不稳定约束时，体系的H是广义能 量积分

Ii）不稳定约束 T = T2 + T1 + T0 = = +   s q T T q T 1 2 2 1      =   = − + s q q T H L  1     = T2 − T0 + V H = T2 － T0 ＋ V= h = const 可见，对于完整的保守力学体系来说，若H中不 显含t，而且体系受不稳定约束时，体系的H是广义能 量积分