
第三章 刚体力学
第三章 刚 体 力 学

导读 ·空间力系和平行力系的求和 ·刚体运动微分方程和平衡方程 ·简单转动惯量的计算 转动惯量的计算
导读 • 空间力系和平行力系的求和 • 刚体运动微分方程和平衡方程 • 简单转动惯量的计算 •转动惯量的计算
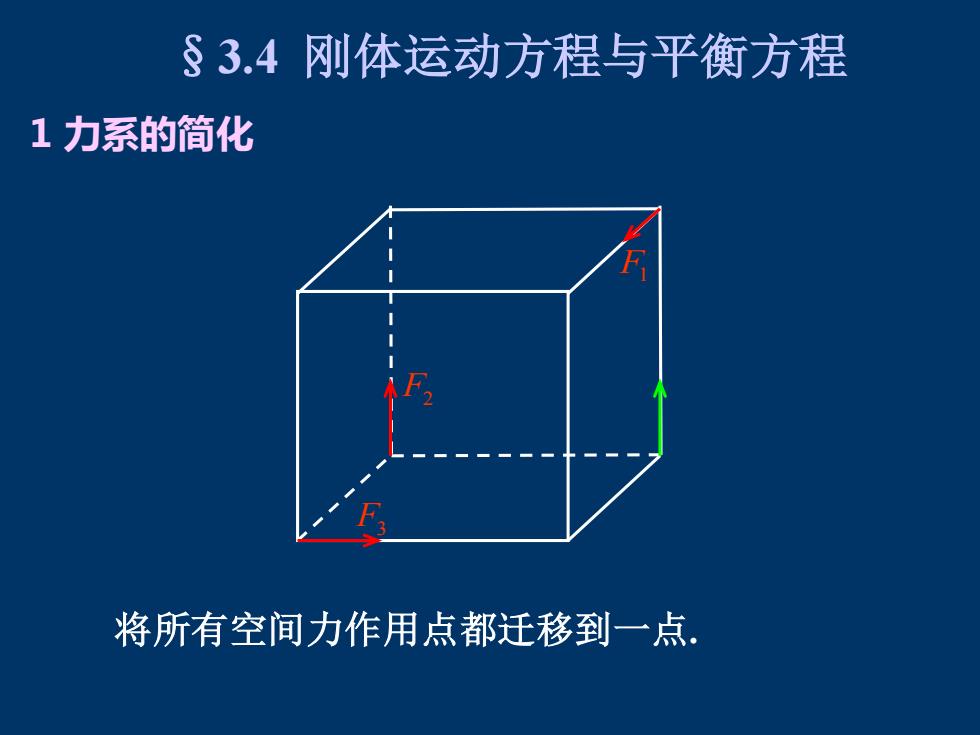
§3.4刚体运动方程与平衡方程 1力系的简化 将所有空间力作用点都迁移到一点
1 力系的简化 将所有空间力作用点都迁移到一点. §3.4 刚体运动方程与平衡方程 F1 F2 F3
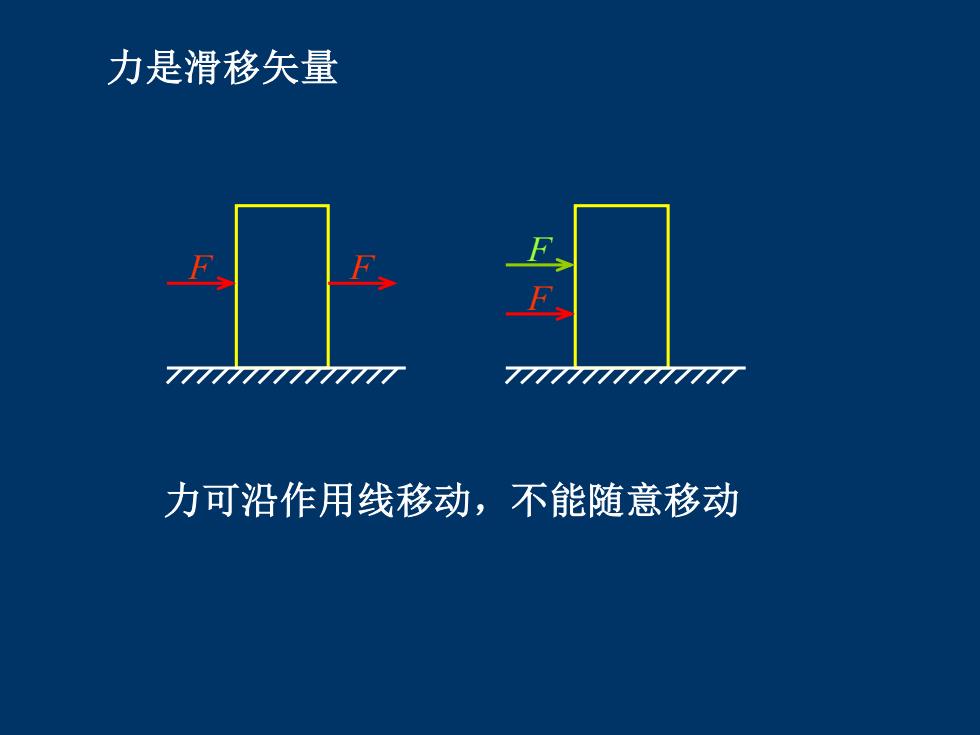
力是滑移矢量 777777777777777 777777777777777 力可沿作用线移动,不能随意移动
力是滑移矢量 力可沿作用线移动,不能随意移动 F F F F

设F为作用在刚体A点上的一个力,P为空间任意一 点,但不在F的作用线上. 在P点添上两个与F的作用线 平行的力F及F2,且 F+五=0,F=F=F 这样F可以化为过P点的力F和F”及F,所组成的 一个力偶
设F’为作用在刚体A点上的一个力, P为空间任意一 点, 但不在F’的作用线上. F’ r A P F2 F1 在P点添上两个与F’的作用线 平行的力F1及F2 , 且 0, ' F1 + F2 = F1 = F2 = F 这样F’可以化为过P点的力F1和F’及F2所组成的 一个力偶

力偶 方向:永远垂直于力偶的作用面 大小:与0点无关。 因此:力偶矩是一自由矢量,可以平行于 自身任意移动位置,不影响其效应
方向:永远垂直于力偶的作用面 大小:与o点无关。 因此:力偶矩是一自由矢量,可以平行于 自身任意移动位置,不影响其效应。 力偶

所以可以把所有空间力化为过一点的力和力偶: P点叫简化中心,力的矢量和叫主矢,力偶矩的矢量 和叫对简化中心的主矩. 主矢使刚体平动状态发生变化 主矩使刚体转动状态发生变化
所以可以把所有空间力化为过一点的力和力偶. 主矢使刚体平动状态发生变化 主矩使刚体转动状态发生变化 P点叫简化中心, 力的矢量和叫主矢, 力偶矩的矢量 和叫对简化中心的主矩

2刚体运动微分方程 如果r代表刚体中任一质点P,对静止系S原点O的位 矢,rc为质心C对O的位矢,而r'为P对质心C的位矢,动 坐标系S随质心作平动,其原点与质心C重合. 则刚体质心C的运动方程为 mi=∑Fo-F
2 刚体运动微分方程 如果ri代表刚体中任一质点Pi 对静止系S原点O的位 矢, rC 为质心C对O的位矢, 而ri ’ 为Pi 对质心C的位矢, 动 坐标系S’随质心作平动, 其原点与质心C重合. mr F F e C i = = ( ) 则刚体质心C的运动方程为

刚体在动坐标系S中的相对运动对质心C的总角动量 满足 方= 对固定坐标系中的定点O,上式仍有效,只需将J改J(对定点 O的总角动量),M改M. 刚体的运动分解随质心的平动十绕质心的转动 M。=F dt M M。=F, M 六个独立的方程 ME。=F M
刚体在动坐标系S’中的相对运动对质心C 的总角动量 满足 J ' M ' = • 对固定坐标系中的定点O, 上式仍有效, 只需将J’改J (对定点 O的总角动量),M’改M. 刚体的运动分解随质心的平动+绕质心的转动 = = = c z c y c x Mz F My F Mx F = = = z z y y x x M dt dJ M dt dJ M dt dJ 六个独立的方程

刚体有六个独立变量.故质心运动及绕质心转动两 组方程式恰好确定刚体的运动情况.也可应用动能原理, 作为一个辅助方程来代替方程中的任意一个. 注意:这时刚体内力所作元功之和为零,故刚体动能的 微分等于刚体在运动过程中外力所作的元功之和
刚体有六个独立变量. 故质心运动及绕质心转动两 组方程式恰好确定刚体的运动情况. 也可应用动能原理, 作为一个辅助方程来代替方程中的任意一个. 注意: 这时刚体内力所作元功之和为零, 故刚体动能的 微分等于刚体在运动过程中外力所作的元功之和