
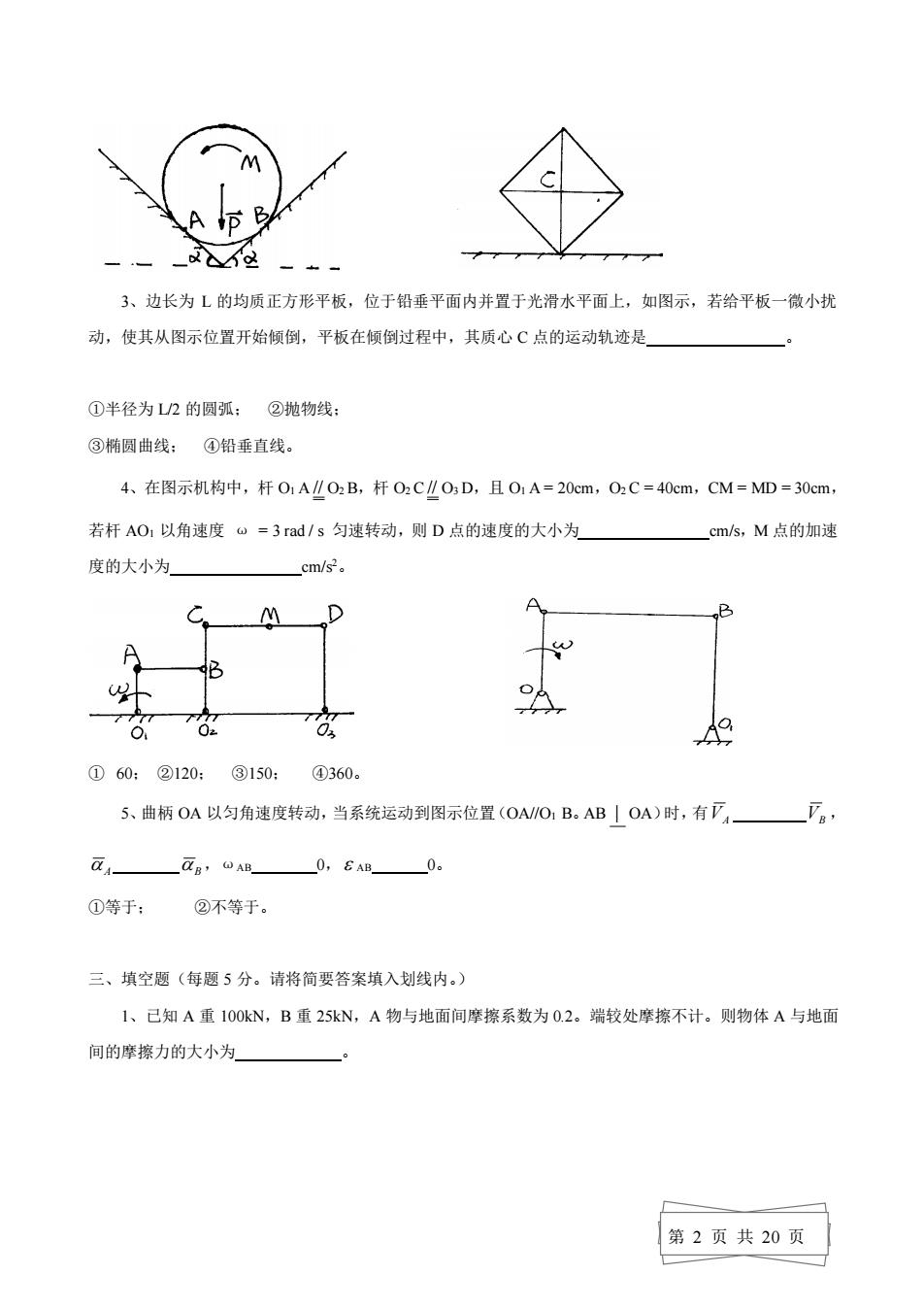
理论力学试题及答案 一、是非题(每题2分。正确用√,错误用×,填入括号内。) 1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡 () 2、力对于一点的矩不因力沿其作用线移动而改变。 () 3、在自然坐标系中,如果速度。=常数,则加速度ā=0。 () 4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。 () 5、设一质点的质量为m,其速度可与x轴的夹角为a,则其动量在x轴上的投影为mvx=mvcosa () 二、选择题(每题3分。请将答案的序号填入划线内。) 1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是 ①主矢等于零,主矩不等于零: ②主矢不等于零,主矩也不等于零 ③主矢不等于零,主矩等于零: ④主矢等于零,主矩也等于零。 2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时(如图),圆柱处于极限 平衡状态。此时按触点处的法向反力N与NB的关系为 ①NA=NB:②NA>Ng:③NA<N 第1页共20页
第 1 页 共 20 页 理论力学试题及答案 一、是非题(每题 2 分。正确用√,错误用×,填入括号内。) 1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。 ( ) 2、力对于一点的矩不因力沿其作用线移动而改变。 ( ) 3、在自然坐标系中,如果速度υ = 常数,则加速度α = 0。 ( ) 4 、 虚 位 移 是偶 想 的 , 极微 小 的 位移 , 它 与时 间 , 主 动力 以 及 运动 的 初 始 条件 无 关 。 ( ) 5、设一质点的质量为 m,其速度 与 x 轴的夹角为α,则其动量在 x 轴上的投影为 mvx =mvcos a 。 ( ) 二、选择题(每题 3 分。请将答案的序号填入划线内。) 1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是 。 ①主矢等于零,主矩不等于零; ②主矢不等于零,主矩也不等于零; ③主矢不等于零,主矩等于零; ④主矢等于零,主矩也等于零。 2、重 P 的均质圆柱放在 V 型槽里,考虑摩擦柱上作用一力偶,其矩为 M 时(如图),圆柱处于极限 平衡状态。此时按触点处的法向反力 NA 与 NB的关系为 。 ①NA = NB; ②NA > NB; ③NA < NB
A IP 3、边长为L的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰 动,使其从图示位置开始倾倒,平板在顿倒过程中,其质心C点的运动轨迹是 ①半径为U2的圆弧:②抛物线: ③椭圆曲线:④铅垂直线。 4、在图示机构中,杆O1A∥02B,杆O2CL0D,且O1A=20cm,O2C=40cm,CM=MD=30cm, 若杆AO:以角速度“=3rd/s匀速转动,则D点的速度的大小为 _cms,M点的加速 度的大小为 A ①60:②120:③150:④360. 5、曲柄OA以匀角速度转动,当系统运动到图示位置(OAWO1B。AB I OA)时,有厂 ①等于: ②不等于。 三、填空题(每题5分。请将简要答案填入划线内。) 1、己知A重100kN,B重25kN,A物与地面间摩擦系数为0.2。端较处摩擦不计。则物体A与地面 间的摩擦力的大小为 第2页共20页
第 2 页 共 20 页 3、边长为 L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰 动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心 C 点的运动轨迹是 。 ①半径为 L/2 的圆弧; ②抛物线; ③椭圆曲线; ④铅垂直线。 4、在图示机构中,杆 O1 A // O2 B,杆 O2 C // O3 D,且 O1 A = 20cm,O2 C = 40cm,CM = MD = 30cm, 若杆 AO1 以角速度 ω = 3 rad / s 匀速转动,则 D 点的速度的大小为 cm/s,M 点的加速 度的大小为 cm/s2。 ① 60; ②120; ③150; ④360。 5、曲柄 OA 以匀角速度转动,当系统运动到图示位置(OA//O1 B。AB | OA)时,有 VA VB , A B ,ωAB 0, AB 0。 ①等于; ②不等于。 三、填空题(每题 5 分。请将简要答案填入划线内。) 1、已知 A 重 100kN,B 重 25kN,A 物与地面间摩擦系数为 0.2。端较处摩擦不计。则物体 A 与地面 间的摩擦力的大小为
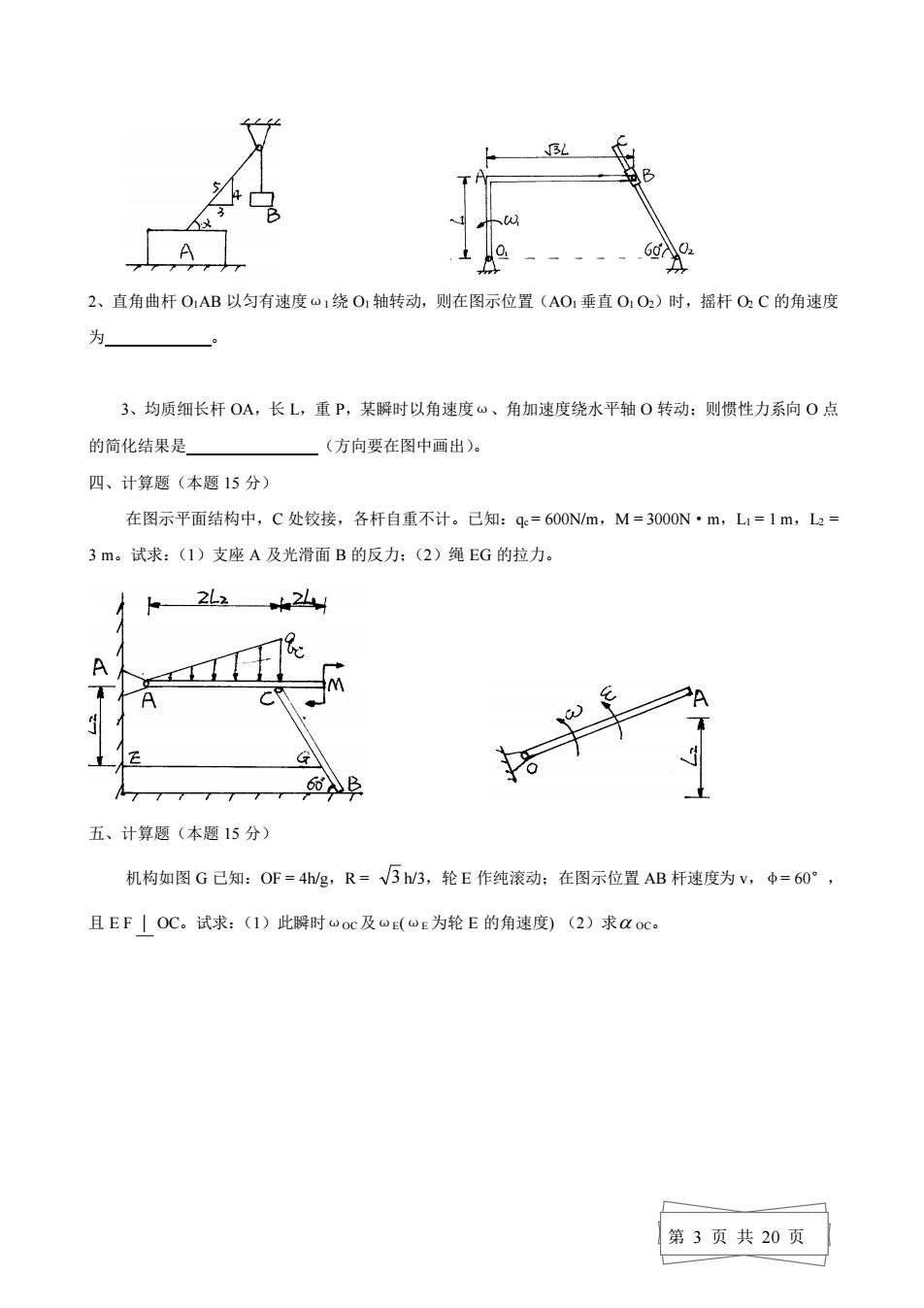
A 2、直角曲杆OAB以匀有速度w1绕O1轴转动,则在图示位置(AO1垂直O1O2)时,摇杆O2C的角速度 为 3、均质细长杆O,长L,重P,某瞬时以角速度。、角加速度绕水平轴0转动:则惯性力系向0点 的简化结果是 (方向要在图中画出)。 四、计算题(本题15分) 在图示平面结构中,C处铰接,各杆自重不计。己知:4=600NWm,M=3000N·m,L1=1m,L2 3m。试求:(1)支座A及光滑面B的反力:(2)绳EG的拉力。 2A 五、计算题(本题15分) 机构如图G已知:OF=4hg,R=√3hW3,轮E作纯滚动:在图示位置AB杆速度为v,中=60°, 且EF|OC。试求:(1)此瞬时ooc及oE(uE为轮E的角速度)(2)求以oc。 第3页共20页
第 3 页 共 20 页 2、直角曲杆 O1AB 以匀有速度ω1 绕 O1 轴转动,则在图示位置(AO1 垂直 O1 O2)时,摇杆 O2 C 的角速度 为 。 3、均质细长杆 OA,长 L,重 P,某瞬时以角速度ω、角加速度绕水平轴 O 转动;则惯性力系向 O 点 的简化结果是 (方向要在图中画出)。 四、计算题(本题 15 分) 在图示平面结构中,C 处铰接,各杆自重不计。已知:qc = 600N/m,M = 3000N·m,L1 = 1 m,L2 = 3 m。试求:(1)支座 A 及光滑面 B 的反力;(2)绳 EG 的拉力。 五、计算题(本题 15 分) 机构如图 G 已知:OF = 4h/g,R = 3 h/3,轮 E 作纯滚动;在图示位置 AB 杆速度为 v,φ= 60°, 且 E F | OC。试求:(1)此瞬时ωOC及ωE(ωE 为轮 E 的角速度) (2)求 OC

=A立疑 () 六、计算题(本题12分) 在图示机构中,己知:匀质轮C作纯滚动,半径为r、重为P,鼓轮B的内径为r、外径为R,对其 中心抽的回转半径为p,重为Pa,物A重为P。绳的CE段与水平面平行,系统从静止开始运动。试求: 物块A下落s距离时轮C中心的速度 七、计算题(本题18分) 机构如图,已知:匀质轮0沿倾角为B的固定斜面作纯滚动,重为P、半径为R,匀质细杆OA重Q, 长为,且水平初始的系统静止,忽略杆两端A,0处的摩擦,试求:(1)轮的中心0的加速度a。(2)用 达朗伯原理求A处的约束反力及B处的摩擦力(将这二力的大小用加速度ā表示即可)。 2 一、结构如图所示,由AB、BC杆件构成,C端放在理想光滑水平面上,AB杆上作用力偶M, BC杆上作用均布载荷q,己知F=1OKN,M=5KNm,q=2KNWm,各杆自重不计,试求A、 C处约束反力以及销钉B对BC杆作用力。 图2分 仁个方程2分 2n1 解: 分共20页
第 4 页 共 20 页 六、计算题(本题 12 分) 在图示机构中,已知:匀质轮 C 作纯滚动,半径为 r、重为 PC,鼓轮 B 的内径为 r、外径为 R,对其 中心轴的回转半径为 ,重为 PB,物 A 重为 PA。绳的 CE 段与水平面平行,系统从静止开始运动。试求: 物块 A 下落 s 距离时轮 C 中心的速度。 七、计算题(本题 18 分) 机构如图,已知:匀质轮 O 沿倾角为β的固定斜面作纯滚动,重为 P、半径为 R,匀质细杆 OA 重 Q, 长为,且水平初始的系统静止,忽略杆两端 A,O 处的摩擦,试求:(1)轮的中心 O 的加速度α。(2)用 达朗伯原理求 A 处的约束反力及 B 处的摩擦力(将这二力的大小用加速度α表示即可)。 一、结构如图所示,由 AB 、BC 杆件构成,C 端放在理想光滑水平面上,AB 杆上作用力偶 M , BC 杆上作用均布载荷 q ,已知 F =10KN,M = 5KNm,q = 2KN m ,各杆自重不计,试求 A 、 C 处约束反力以及销钉 B 对 BC 杆作用力。 图 2 分 一个方程 2 分 解: A B C F M 2m 2m 2m q 45

以BC杆为对象: ∑M。=0,E2-q-225=-0 Fc=4kN ∑F=0,F-g-22.5=0 2 Σ5=0,5-9259-0 Fay=0 459 以AB梁为对象: ∑F=0,Fa-F=0 2m F =4kN ∑F=0,F-F-F=0 F=10kN ∑M1=0,M,+M-F.4=0 4m M =35kN.m 二、OA杆长h,绕O轴定轴转动,带动长为h的套筒AB在OD杆上滑动。若设置如图所 示的参考基=[民可,杆OA的连体基=[氏可,套筒AB的连体基=民]「,并 假设,为第1个构件上待求点相对于参考基的坐标阵,。为基点坐标阵,A,为第1个构件连体 基相对于参考基的方向余弦阵,P,为构件i上待求点 相 对于自身连体基的坐标阵,试利用关系式 ”=o+AP,写出机构运动到图示位形时: (1)OA杆和套筒AB相对于参考基的位形: (2)套简AB的上B点相对于参考基的位置坐标阵。 DA杆位形5分,套筒AB位形5分 人60° 0 B点相对于参考基的位置坐标阵5分 第5页共20页
第 5 页 共 20 页 以 BC 杆为对象: MB = 0, FC 2−q2 2 2 = 0 FC = 4kN Fx = 0, 0 2 2 FBx − q 2 2 = Fy = 0, 0 2 2 FBy − q 2 2 + FC = FBy = 0 以 AB 梁为对象: Fx = 0, FAx − FBx = 0 FAx = 4kN Fy = 0, FAy − FBy − F = 0 FAy =10kN MA = 0, MA + M − F 4 = 0 MA = 35kNm 二、OA 杆长 l1,绕 O 轴定轴转动,带动长为 l2 的套筒 AB 在 O1D 杆上滑动。若设置如图所 示的参考基 T [x y] e = ,杆 OA 的连体基 T 1 1 [x y] e = ,套筒 AB 的连体基 T 2 2 2 [x y ] e = ,并 假设 i r 为第 i 个构件上待求点相对于参考基的坐标阵, O r 为基点坐标阵, Ai 为第 i 个构件连体 基相对于参考基的方向余弦阵, ρi 为构件 i 上待求点 相 对 于 自 身 连 体 基 的 坐 标 阵 , 试 利 用 关 系 式 A O Aiρi r = r + 写出机构运动到图示位形时: (1) OA 杆和套筒 AB 相对于参考基的位形; (2)套筒 AB 的上 B 点相对于参考基的位置坐标阵。 OA 杆位形 5 分,套筒 AB 位形 5 分 B 点相对于参考基的位置坐标阵 5 分 B q FBx FBy FC C 45 2m FAy FAx A M A FBx FBy B 4m M F O x y 1 x 1 y 2 x 2 y A 60 45 B O1 D

解:图示瞬时方向余弦阵 A=[os450-sm451-[22-2/21 ms6及2A- 9][阳品-日 (1)OA杆的位形g=00π14 -[船周-日ka-k8周 销8的形-为-1-[竖哥 (②)B点的位置坐标阵 √2, V3 1/2 2+3,) (W21-12) 三、半径为r的圆盘与长度为I的直杆AB在盘心A铰接,圆盘沿水平面纯滚,AB杆B端沿 铅直墙壁滑动。在图示位置,圆盘的角速度为),角加速度为α,杆与水平面的夹角为0, 试求该瞬时杆端B的速度和加速度。 解:()球速度,速度瞬心C如图 AC=Isin0,BC=Icos0 4=0(2分) lomeigra-ct (2分) (图1分) 第6页共20页
第 6 页 共 20 页 解:图示瞬时方向余弦阵 − = − = 2 / 2 2 / 2 2 / 2 2 / 2 sin 45 cos45 cos45 sin 45 A1 , = 0 1 1 l − = − − − − − = 1/ 2 3 / 2 3 / 2 1/ 2 sin( 30 ) cos( 30 ) cos( 30 ) sin( 30 ) A2 , = 0 2 2 l (1) OA 杆的位形 T q1 = 0 0 / 4 = + = − + = 2 / 2 2 / 2 2 / 2 2 / 2 0 0 2 / 2 2 / 2 0 2 / 2 2 / 2 1 1 1 1 1 l l l l l y x y x O O A A 套筒 AB 的位形 T 1 1 T 1 2 6 2 2 2 / 6 = − = − q x y l l A A (2) B 点的位置坐标阵 − + = − + = − + = ( 2 ) ( 2 3 ) 2 1 2 3 2 2 2 2 1/ 2 3 / 2 0 3 / 2 1/ 2 2 1 2 1 2 1 2 1 2 2 1 1 2 l l l l l l l l l y x y x A A B B 三、半径为 r 的圆盘与长度为 l 的直杆 AB 在盘心 A 铰接,圆盘沿水平面纯滚,AB 杆 B 端沿 铅直墙壁滑动。在图示位置,圆盘的角速度为 ,角加速度为 ,杆与水平面的夹角为 , 试求该瞬时杆端 B 的速度和加速度。 解:(1) 球速度,速度瞬心 C 如图 AC = lsin , BC = l cos vA = r (2 分) lsin r AC vA AB = = (2 分) cot sin = = cos = r l r v BC l B AB (2 分) (图 1 分) A B r l
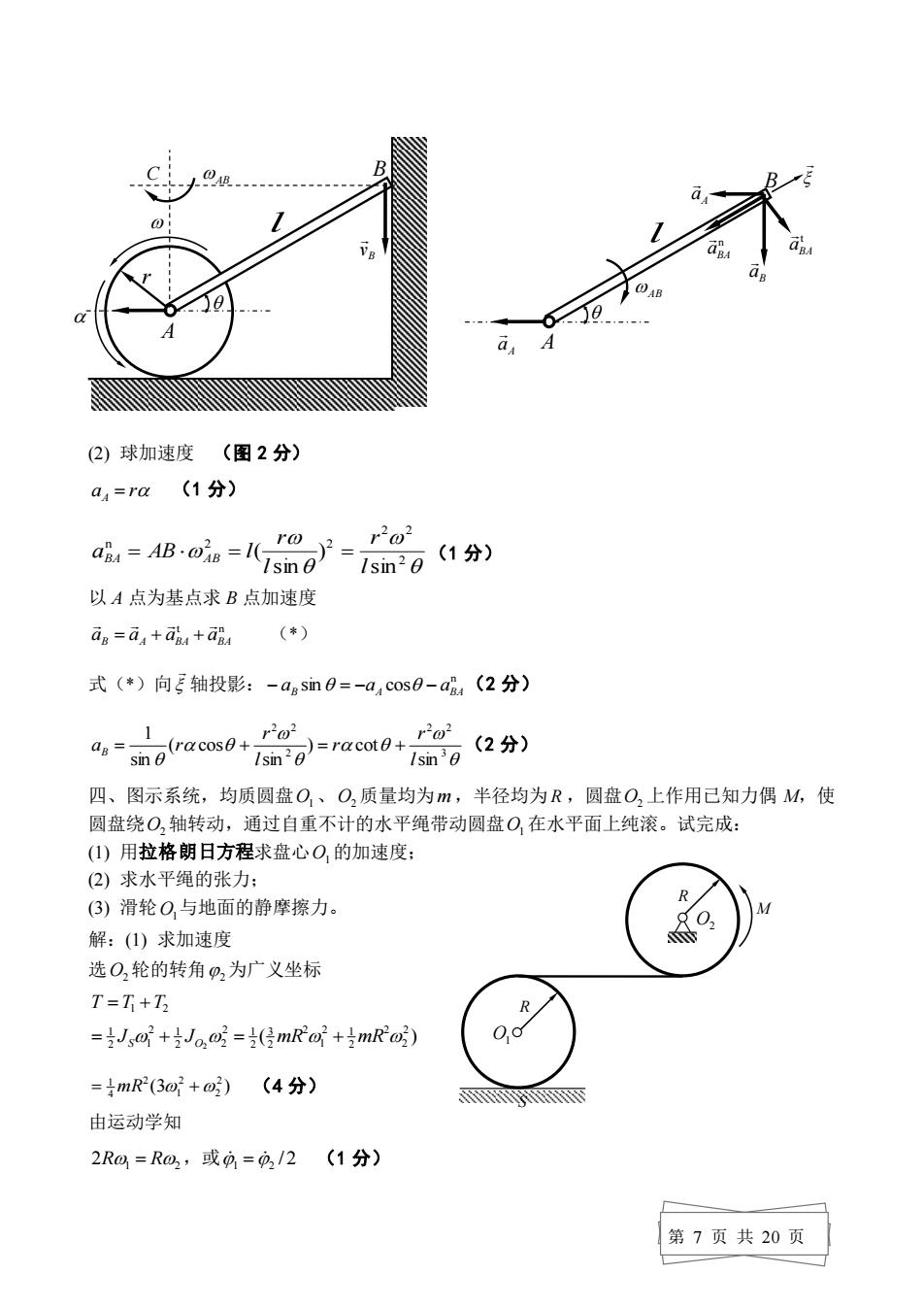
001 (2)球加速度(图2分) a4=ra(1分) i生8o=7g-。 1sn20(1分) 以A点为基点求B点加速度 dg a+am am (*) 式(◆)向E轴投影:-aasin0=-a,cos0-a84(2分) a,0 raowl0+g-aom0+ga》分 ro2 四、图示系统,均质圆盘O,、O,质量均为m,半径均为R,圆盘O,上作用已知力偶M,使 圆盘绕O,轴转动,通过自重不计的水平绳带动圆盘O,在水平面上纯滚。试完成: ()用拉格朗日方程求盘心O,的加速度: 2)求水平绳的张力: (3)滑轮0与地面的静摩擦力。 解:()求加速度 选O,轮的转角0,为广义坐标 T=T+T =J欧+Jo,=(层mRa+mR) =mR2(3a2+)(4分) F 由运动学知 2Ra=R@,或=g/2(1分) 第7页共20页
第 7 页 共 20 页 (2) 球加速度 (图 2 分) aA = r (1 分) 2 2 2 n 2 2 sin ) sin ( l r l r a AB l BA = AB = = (1 分) 以 A 点为基点求 B 点加速度 t n aB aA aBA aBA = + + (*) 式(*)向 轴投影: n sin cos − aB = −aA − aBA (2 分) 3 2 2 2 2 2 sin ) cot sin ( cos sin 1 l r r l r a r B = + = + (2 分) 四、图示系统,均质圆盘 O1、O2 质量均为 m ,半径均为 R ,圆盘 O2 上作用已知力偶 M,使 圆盘绕 O2 轴转动,通过自重不计的水平绳带动圆盘 O1 在水平面上纯滚。试完成: (1) 用拉格朗日方程求盘心 O1 的加速度; (2) 求水平绳的张力; (3) 滑轮 O1 与地面的静摩擦力。 解:(1) 求加速度 选 O2 轮的转角 2 为广义坐标 T = T1 +T2 ( ) 2 2 2 2 2 1 1 2 2 3 2 2 1 2 2 2 1 2 1 1 2 = JS + JO = mR + mR (3 ) 2 2 2 1 2 4 = 1 mR + (4 分) 由运动学知 2R1 = R2 ,或 1 = 2 / 2 (1 分) O1 O2 R R M S A B r l C B v AB A B l AB A a B a A a n BA a t BA a

代入动能T=n6呼+)=m1分) 广义力:0=M(1分) 代入拉氏方程肥-g-Q,有m%=M,得:兵-欲2分) 又由运动学知圆盘的角加速度 负受批 盘心0的加造度马=隔微1分剂 2)求绳的张力(5分) [法一]以O,轮为研究对象 由io=M-FR,即Jo,=M-FR 5-贵-a兴兴兴 F [法二]或以O,轮为研究对象 由i=F2R,即J=F·2R 得:F= mR=3M 7R 2)求摩擦力(5分) 以0,轮为研究对象 [法一]运用质心运动定理 4M 3M M ma=F+Fs, Fs=md-F=M7mR-7R-7R [法二]对动点D运用动量矩定理o+。×。=Mo(F) -JetR-ma)+0=E2R,即-mR项+R-ma=R2R 五、图示机构,在铅垂面内,曲柄OA和连杆AB是相同的均质杆,长OA=AB=1,自重不 计,滑块B重G,曲柄OA上作用一力偶M,使机构静止平衡。已知静止平衡时曲柄OA与 第8页共20页
第 8 页 共 20 页 代入动能得 2 2 2 2 2 2 2 2 4 1 16 7 ) 4 (3 T = mR + = mR (1 分) 广义力: Q 2 = M (1 分) 代入拉氏方程 2 d 2 2 d Q T T t = − ,有 mR 2 = M 2 8 7 ,得: 2 2 7 8 mR M = (2 分) 又由运动学知圆盘的角加速度 2 2 1 7 4 2 mR M = = 盘心 O1 的加速度: mR M aO R 7 4 1 = 1 = (1 分) (2) 求绳的张力(5 分) [法一]以 O2 轮为研究对象 由 LO M FTR 2 = − ,即 JO 2 M FT R 2 = − 得: R M R M R M mR R M F 7 3 7 4 2 1 T = − 2 = − = [法二]或以 O1 轮为研究对象 由 L S = FT 2R ,即 J S 1 = FT 2R 得: R M F mR 7 3 4 3 T = 1 = (2) 求摩擦力(5 分) 以 O1 轮为研究对象 [法一]运用质心运动定理 ma1 = FT + FS, R M R M mR M F ma F m 7 7 3 7 4 S 1 T 2 = − = − = [法二]对动点 D 运用动量矩定理 ( ) 1 LD vD mvO MD F + = dt ( J C R mvO ) 0 FS 2R d 1 − + + = ,即 mR R maO F 2R 2 1 1 S 2 1 − + = 得: R M mR M mR mR M mR R F 7 ) 7 4 2 1 7 4 ( 2 1 2 2 S = − = 五、图示机构,在铅垂面内,曲柄 OA 和连杆 AB 是相同的均质杆,长 OA = AB = l ,自重不 计,滑块 B 重 G ,曲柄 OA 上作用一力偶 M ,使机构静止平衡。已知静止平衡时曲柄 OA 与 M O2 R mg F2 y F2x FT O1 R FT FS mg FN D S
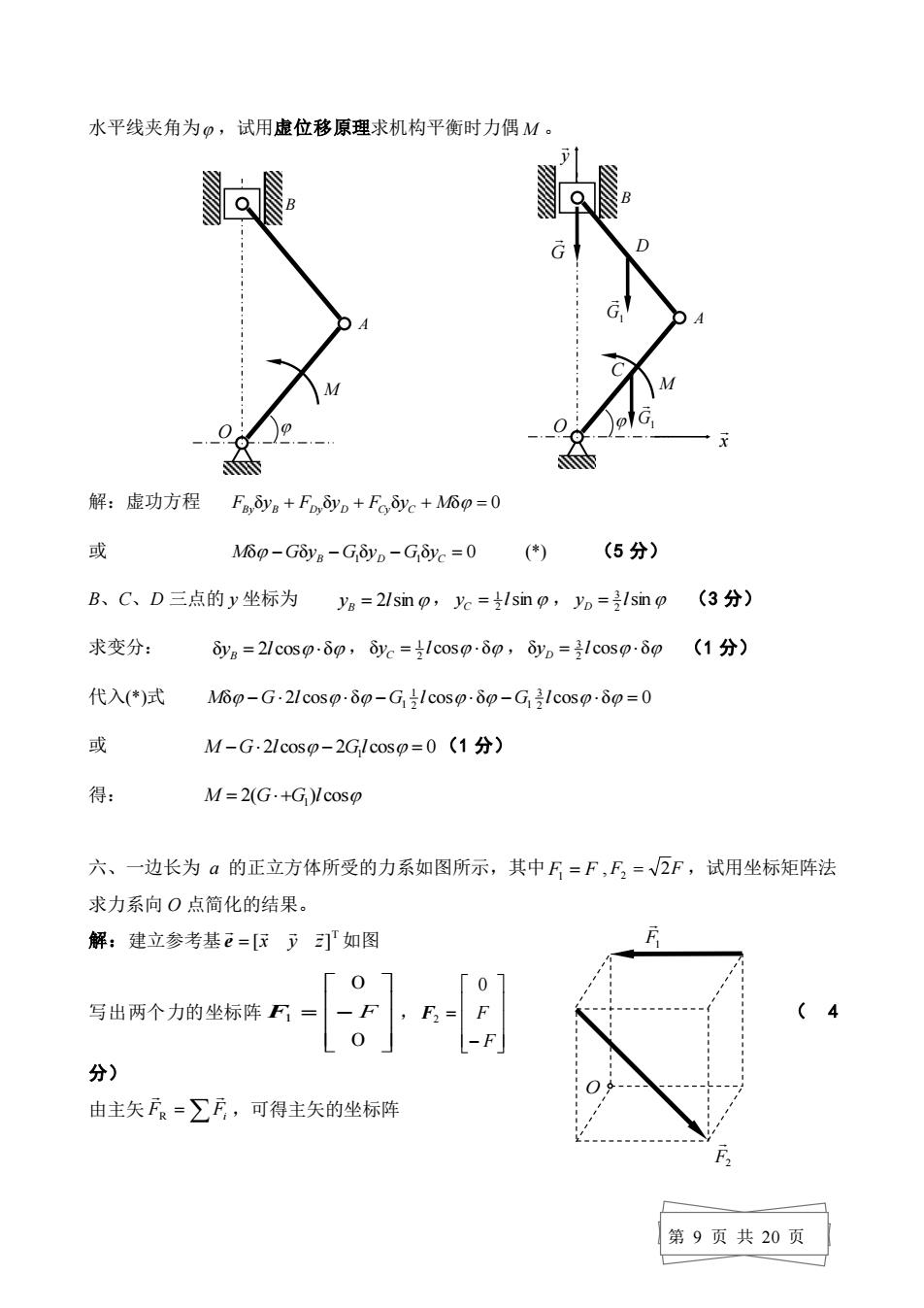
水平线夹角为口,试用虚位移原理求机构平衡时力偶M 解:虚功方程Fya+Fn,yn+Fye+M6p=0 或 M6p-G8ya-Gy。-G,0y.=0((5分) B、C、D三点的y坐标为ya=2 Isin p,c=Isin o,yo=Isnp(3分) 求变分: dya=2 Icosp.δ0,ye=lcosp.δp,yp=lcosδp(1分) 代入(*)试M6g-G.21coso-δp-G,-Icosp-δ0-Glcosp-δp=0 或 M-G.2lcoso-2Glcos=0 ( 得 M=2(G.+G)/cosp 六、一边长为a的正立方体所受的力系如图所示,其中E=F,F=√2F,试用坐标矩阵法 求力系向O点简化的结果。 解:建立参考基e=[下如图 07 0 写出两个力的坐标阵F= d o 分) 由主矢F=∑F,可得主矢的坐标阵 第9页共20页
第 9 页 共 20 页 水平线夹角为 ,试用虚位移原理求机构平衡时力偶 M 。 解:虚功方程 FByδyB + FDyδyD + FCyδyC + Mδ = 0 或 Mδ − GδyB − G1 δyD − G1 δyC = 0 (*) (5 分) B、C、D 三点的 y 坐标为 yB = 2lsin, yC = 1 2 lsin , 2 sin 3 y l D = (3 分) 求变分: δyB = 2l cos δ ,δ 2 cos δ 1 y = l C ,δ 2 cos δ 3 y = l D (1 分) 代入(*)式 δ 2 cos δ cos δ cos δ 0 2 3 2 1 1 M − G l − G1 l − G l = 或 M −G 2l cos − 2G1 l cos = 0 (1 分) 得: M = 2(G+G1 )l cos 六、一边长为 a 的正立方体所受的力系如图所示,其中 F1 = F , F2 = 2F ,试用坐标矩阵法 求力系向 O 点简化的结果。 解:建立参考基 T [x y z] e = 如图 写出两个力的坐标阵 = − 0 0 F1 F , − = F F 0 F2 ( 4 分) 由主矢 F = Fi R ,可得主矢的坐标阵 O A B M O A B M x y G G1 G1 D C F1 O F2

Fa=∑F= 得:F=-FE,即简化所得的力F。=F=-F三 (1分) 假设各力作用点的位置矢量和万,对应的坐标阵 「b b 由此写出坐标方阵 「0-bb =600,68.0b2分) L-b00 0b0 主矩M。=∑M(何,对应的坐标阵M。=M,+M,=E+元E 「0-bbT01「bF -b0000 L0 b 0-F 6F 这样得:Mo=M+M2=0+ 即主矩:M。=bF+bF:(2分) 简化的结果是一个力和一个力偶,这个力矢量和力偶矩矢量为: Fo=FR=-F三,Mo=bF+bF 七、质量不计的圆环如图,在径向焊接一个质量为m、长为,的均质细棒,圆环可在水平面 上纯滚,求系统的运动微分方程。 (提示:余弦定理:c2=a2+b2-2 abcosp:sim(π-p)=sinp) 解: 法一]选圆环的转角口为广义坐标,圆环的角速度为0。 (①)运动分析: 0页
第 10 页 共 20 页 − = − + = = − F F i F F 0 0 0 0 0 FR F (2 分) 得: F F z R = − ,即简化所得的力 F F F z O = R = − (1 分) 假设各力作用点的位置矢量 1 r 和 2 r ,对应的坐标阵 = b b 0 1 r , = b b 0 2 r (2 分) 由此写出坐标方阵 − − = 0 0 0 0 0 ~ 1 b b b b r , − − = 0 0 0 0 0 ~ 2 b b b b r (2 分) 主矩 M =M (F) O O ,对应的坐标阵 1 2 1 1 2 2 ~ ~ MO = M + M = r F + r F = − − − = 0 0 0 0 0 0 0 0 0 ~ 1 1 bF F b b b b r F , − = − − − = bF bF bF F F b b b b 0 0 0 0 0 0 ~ 2F2 r (2 分) 这样得: = − + = + = bF bF bF bF bF bF O 0 0 M M1 M2 0 即主矩: M bF y bF z O = + (2 分) 简化的结果是一个力和一个力偶,这个力矢量和力偶矩矢量为: F F F z O = R = − , M bF y bF z O = + 七、质量不计的圆环如图,在径向焊接一个质量为 m、长为 r 的均质细棒,圆环可在水平面 上纯滚,求系统的运动微分方程。 (提示:余弦定理: 2 cos 2 2 2 c = a + b − ab ; sin( −) = sin ) 解: [法一]选圆环的转角 为广义坐标,圆环的角速度为 。 (1) 运动分析: F1 O F2 x y z 1 r 2 r