
第七章应力和应变分析 强度理论 §7-1应力状态概述 §7-2平面应力状态分析-解析法 §7-3平面应力状态分析-图解法 §74三向应力状态分析 用 §7-5平面应变状态分析 品 §7-6广义胡克定律6则 §77复杂应力状态的变形比能 §7-8强度理论 §7-9莫尔强度理论
第七章 应力和应变分析 强度理论 §7-1 应力状态概述 §7-2 平面应力状态分析-解析法 §7-3 平面应力状态分析-图解法 §7-4 三向应力状态分析 §7-6 广义胡克定律 §7-7 复杂应力状态的变形比能 §7-8 强度理论 §7-5 平面应变状态分析 §7-9 莫尔强度理论

§7-1应力状态概述 应力状态的概念 新用册均 面翻 1.低碳钢和铸铁的拉伸实验 按河百川 大遥置弘函 2.低碳钢和铸铁的扭转实验
§7-1 应力状态概述 一、应力状态的概念 1.低碳钢和铸铁的拉伸实验 2.低碳钢和铸铁的扭转实验

低碳钢和铸铁的拉伸 大道弘函图 低碳钢 铸铁 塑性材料拉伸时为什么会出现滑移线?
低碳钢 塑性材料拉伸时为什么会出现滑移线? 铸铁 低碳钢和铸铁的拉伸

低碳钢和铸铁的扭转 内 大置弘面 低碳钢 铸铁 为什么脆性材料扭转时沿45螺旋面断开?
为什么脆性材料扭转时沿45°螺旋面断开? 低碳钢和铸铁的扭转 低碳钢 铸铁

3.重要结论 (1)拉中有剪,剪中有拉; (2)不仅横截面上存在应力,斜截面上也存在应力; (3)同一面上不同点的应力各不相同; 〔4)同一点不同方向面上的应力也是各不相同 调 应力 册品标 哪个面上? 哪一点? 哪点? 德纳百川 哪个方向面? 大道弘 4.一点的应力状态 过一点不同方向面上应力的情况,称之为这一点的应力状 态亦指该点的应力全貌
(1)拉中有剪,剪中有拉; (2)不仅横截面上存在应力,斜截面上也存在应力; (3)同一面上不同点的应力各不相同; (4) 同一点不同方向面上的应力也是各不相同 3.重要结论 哪一点? 哪个方向面? 应 力 哪一个面上? 哪一点? 4.一点的应力状态 过一点不同方向面上应力的情况,称之为这一点的应力状 态,亦指该点的应力全貌
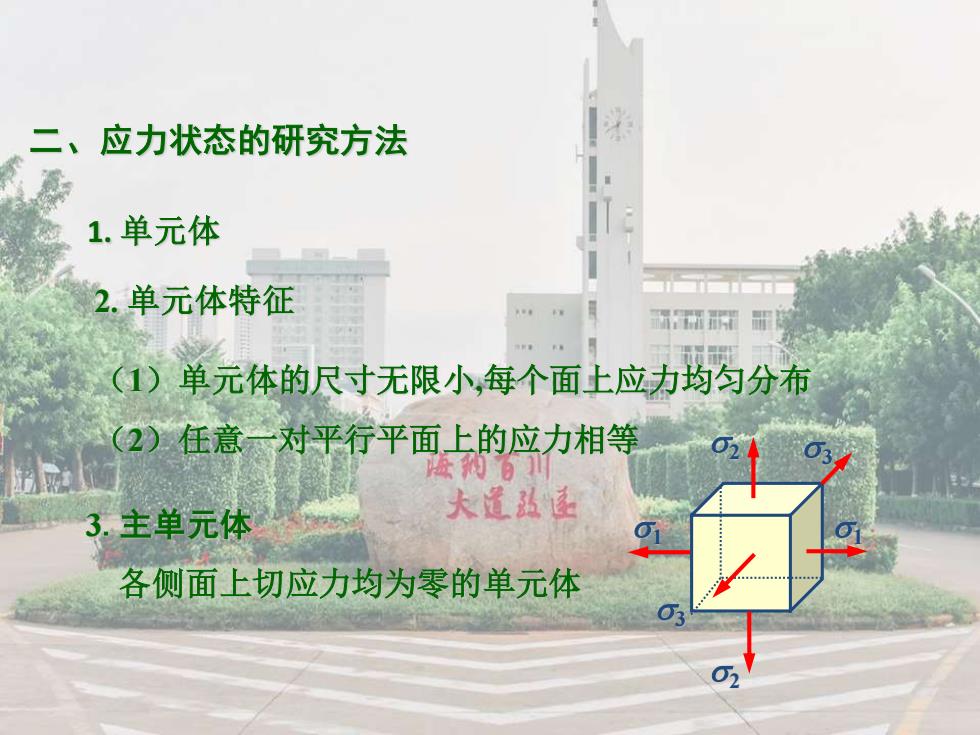
二、应力状态的研究方法 1.单元体 2.单元体特征 所际部均 (1)单元体的尺寸无限小,每个面上应力均匀分布 (②)任意一对平行平面上的应力相等 阳。门 3.主单元体 大遥弘面 各侧面上切应力均为零的单元体
二、应力状态的研究方法 1. 单元体 (2)任意一对平行平面上的应力相等 2. 单元体特征 3.主单元体 各侧面上切应力均为零的单元体 (1)单元体的尺寸无限小,每个面上应力均匀分布 3 1 2 2 3 1
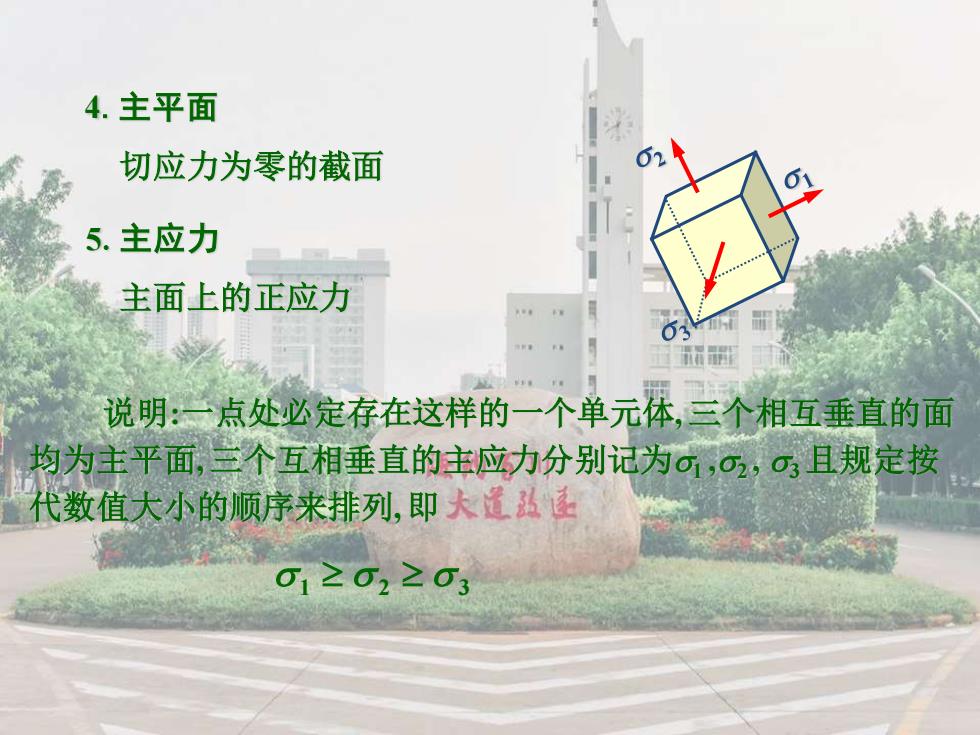
4.主平面 切应力为零的截面 5.主应力 主面上的正应力 0 说明:一点处必定存在这样的一个单元体,三个相互垂直的面 均为主平面,三个互相垂直的主应力分别记为©,o2,σ?且规定按 代数值大小的顺序来排列,即大道弘孟 01≥02≥03
4.主平面 切应力为零的截面 5.主应力 主面上的正应力 说明:一点处必定存在这样的一个单元体, 三个相互垂直的面 均为主平面, 三个互相垂直的主应力分别记为1 ,2 , 3 且规定按 代数值大小的顺序来排列, 即 1 2 3
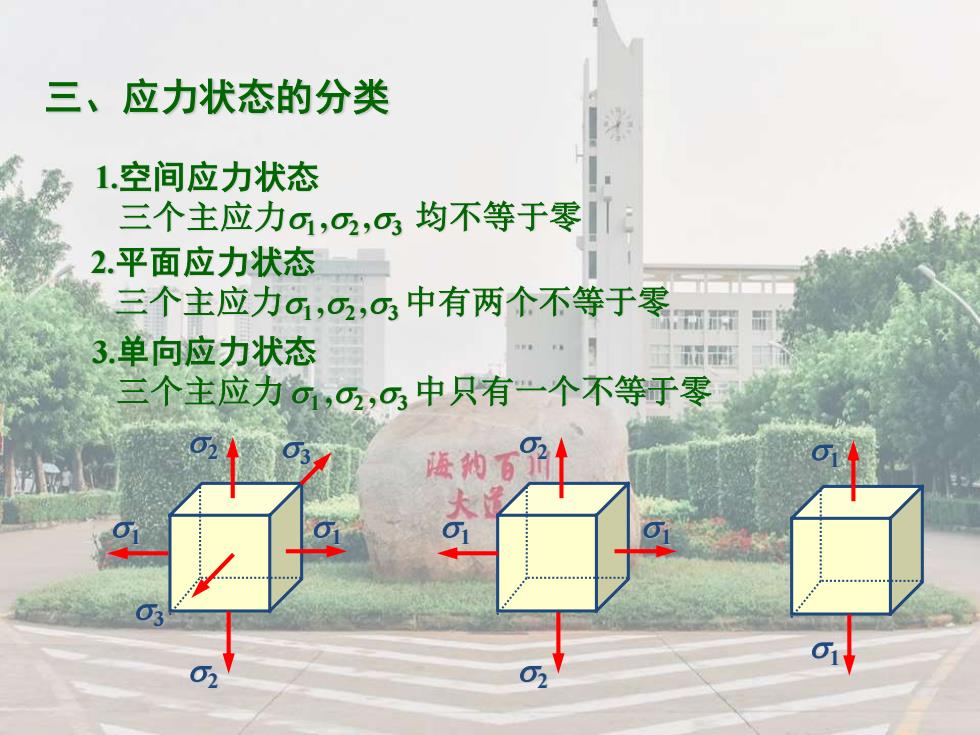
三、应力状态的分类 1.空间应力状态 三个主应力,02,03均不等于零 2.平面应力状态 三个主应力,2,中有两个不等于零量 3.单向应力状态 别 个主应力61,C2,03中只有一个不等于零 遜物
三、应力状态的分类 1.空间应力状态 三个主应力1 ,2 ,3 均不等于零 2.平面应力状态 三个主应力1 ,2 ,3 中有两个不等于零 3.单向应力状态 三个主应力1 ,2 ,3 中只有一个不等于零 3 1 2 2 3 1 2 2 1 1 1 1
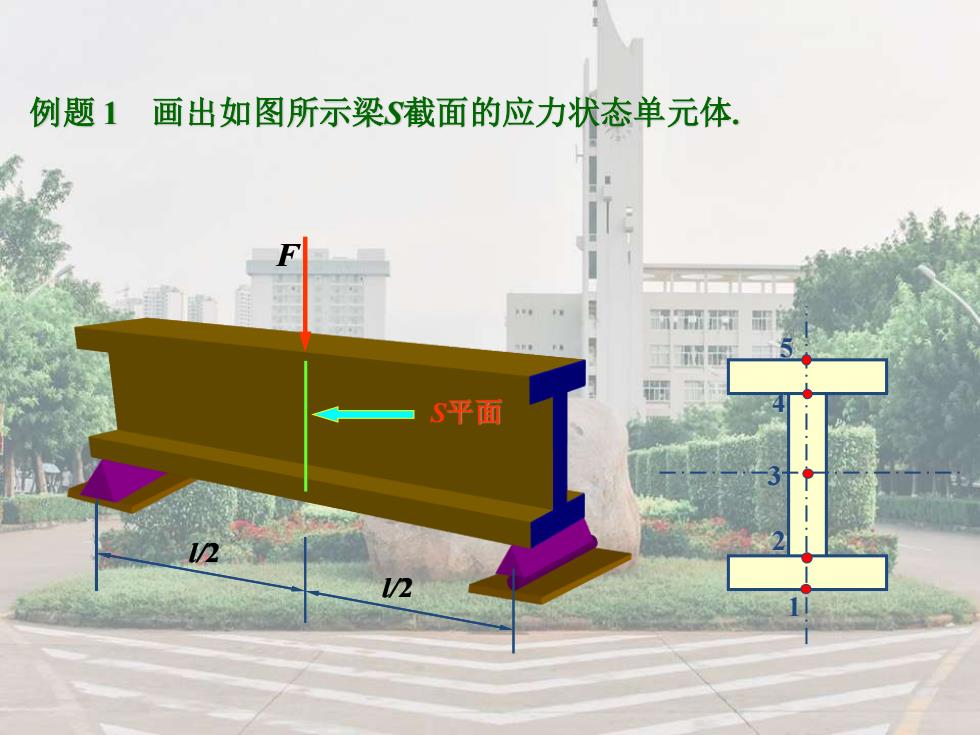
例题1画出如图所示梁S截面的应力状态单元体 研 猫 S平面 2
例题 1 画出如图所示梁S截面的应力状态单元体. 5 4 3 2 1 F l/2 l/2 l/2 l/2 S平面
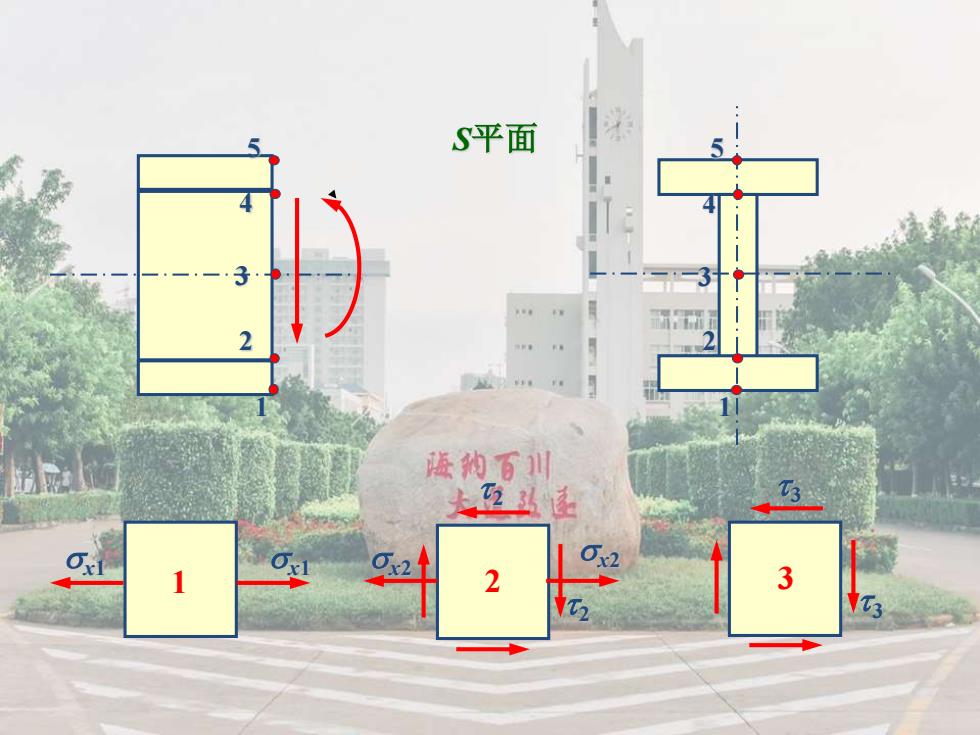
S平面 德纳百川 互站超 021 02 1 2 3
S平面 2 5 4 3 2 1 5 4 3 2 1 1 x1 x1 x2 x2 2 2 3 3 3