
第三章 刚体力学 §3.4F 刚体运动方程与平衡方程 超卓谋程
第三章 刚体力学 §3.4 刚体运动方程与平衡方程

§3.4 刚体运动方程与平衡方程 导读 ·空间力系和平行力系的求和 ·刚体运动微分方程和平衡方程 超卓课程
导读 • 空间力系和平行力系的求和 • 刚体运动微分方程和平衡方程 §3.4 刚体运动方程与平衡方程
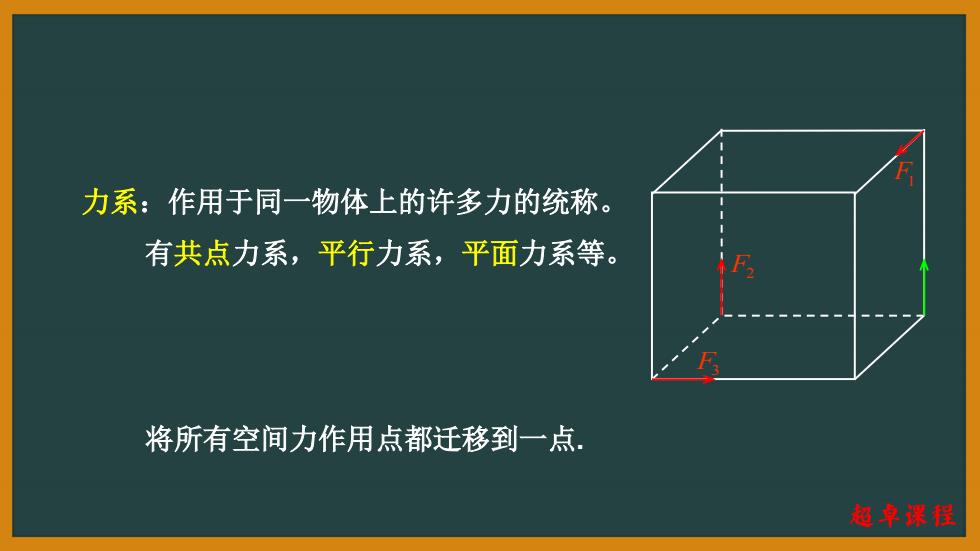
力系:作用于同一物体上的许多力的统称。 有共点力系,平行力系,平面力系等。 将所有空间力作用点都迁移到一点 超卓谋程
将所有空间力作用点都迁移到一点. F1 F2 F3 力系:作用于同一物体上的许多力的统称。 有共点力系,平行力系,平面力系等
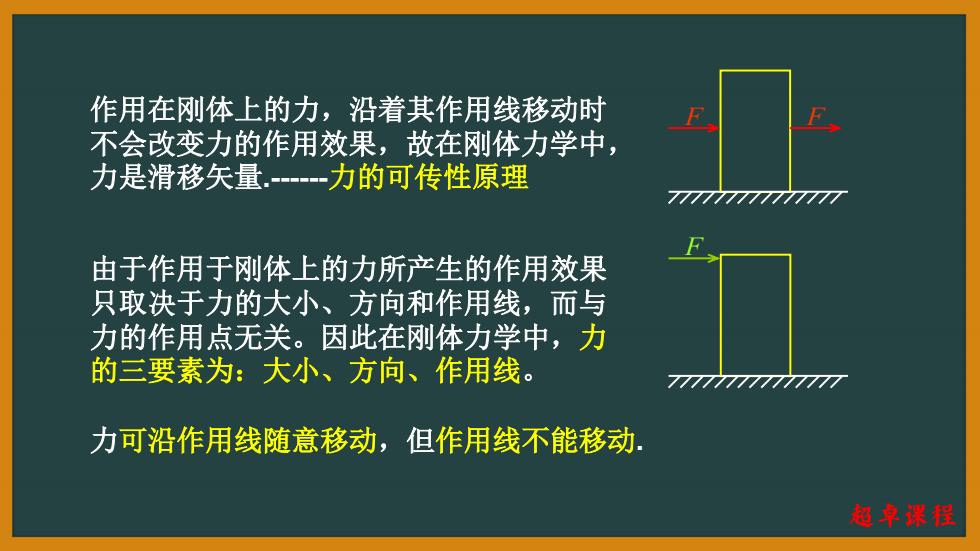
作用在刚体上的力,沿着其作用线移动时 不会改变力的作用效果,故在刚体力学中, 力是滑移矢量.-力的可传性原理 由于作用于刚体上的力所产生的作用效果 只取决于力的大小、方向和作用线,而与 力的作用点无关。因此在刚体力学中,力 的三要素为:大小、方向、作用线。 力可沿作用线随意移动,但作用线不能移动: 超卓课程
力可沿作用线随意移动,但作用线不能移动. F F F 作用在刚体上的力,沿着其作用线移动时 不会改变力的作用效果,故在刚体力学中, 力是滑移矢量.-力的可传性原理 由于作用于刚体上的力所产生的作用效果 只取决于力的大小、方向和作用线,而与 力的作用点无关。因此在刚体力学中,力 的三要素为:大小、方向、作用线

1力系的简化 共点力系:平行四边形法则,简化为一个单力. 平面非平行力系:力的可传性原理+平行四边形法则,可简化为单力 平面平行力系:力的作用线可用力矩关系确定 空间平行力系:与上相同. 特殊的共面平行力系:力偶=-F, 超卓谋程
1 力系的简化 共点力系:平行四边形法则,简化为一个单力. 平面平行力系:力的作用线可用力矩关系确定. 平面非平行力系:力的可传性原理+平行四边形法则,可简化为单力. 特殊的共面平行力系:力偶 空间平行力系:与上相同

力偶对任意点O的力矩: M=元xE+万,×瓦=万×(E)+万xF =(-)x,=F×F(匠方向沿E,方向) M的大小:M=M=rFsin0=Fd M的方向:垂直力偶的作用面,服从右手螺旋法则。 M与取矩点O无关,故称为自由矢量, 力偶无平动效应,只有转动效应.力偶矩是力偶唯一的力学效果, 力偶矩是自由矢量,可以平行于自身、任意移动位置,不影响其效果, 超卓课程
力偶无平动效应, 只有转动效应. 力偶矩是力偶唯一的力学效果. 力偶矩是自由矢量,可以平行于自身、任意移动位置,不影响其效果. 力偶 A B d r 2 r 1 r o 对任意点O的力矩: 与取矩点O无关,故称为自由矢量
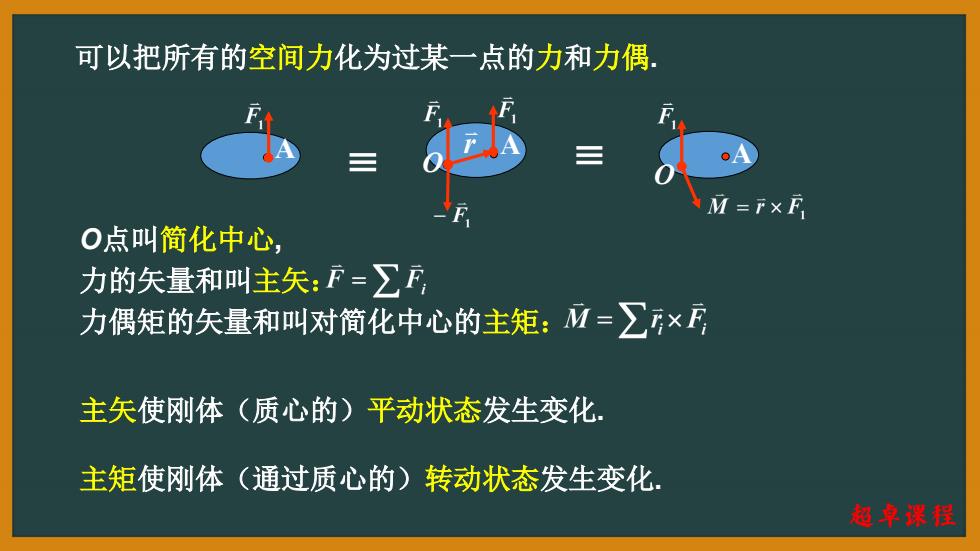
可以把所有的空间力化为过某一点的力和力偶 M=F×F O点叫简化中心, 力的矢量和叫主矢:F=∑F 力偶矩的矢量和叫对简化中心的主矩:M=∑× 主矢使刚体(质心的)平动状态发生变化, 主矩使刚体(通过质心的)转动状态发生变化, 超卓谋程
可以把所有的空间力化为过某一点的力和力偶. 主矢使刚体(质心的)平动状态发生变化. 主矩使刚体(通过质心的)转动状态发生变化. O点叫简化中心, 力的矢量和叫主矢: 力偶矩的矢量和叫对简化中心的主矩: A O A O A

2 列体运动微分方程 如果r代表刚体中任一质点P,对静止系S原点O的 位矢,r为质心C对O的位矢,动坐标系S随质心作平 动,其原点与质心C重合,r'为P对质心C的位矢 质心C的运动方程为 mi成e=∑Fe-F 刚体在动坐标系S中的相对运动,角动量满足 J-M 对固定坐标系中的定点0,形式仍有效为:广=M 超卓课程
2 刚体运动微分方程 如果ri代表刚体中任一质点Pi 对静止系S原点O的 位矢, rC为质心C对O的位矢, 动坐标系S’随质心作平 动, 其原点与质心C重合, ri ’ 为Pi 对质心C的位矢. mr F F e C i ( ) 质心C的运动方程为 刚体在动坐标系S’中的相对运动,角动量满足 J ' M ' 对固定坐标系中的定点O ,形式仍有效为: y x z x’ y’ z’ rC ri . P O C ri ’

刚体的运动分解随质心的平动十绕质心的转动 dJ m。=F =M's dt mye=Fy -=M) 六个独立的方程 dt mi。=F: =M: dt 刚体有六个独立变量.故质心运动及绕质心转动两组方程式 恰好确定刚体的运动情况,就是刚体运动的基本微分方程 可用动能定理d7-∑r⊙.d,作为一个辅助方程来代替方程中的 任意一个.注意:刚体内力所作元功之和为零,故刚体动能的微分 等于刚体在运动过程中外力所作的元功之和 超卓谋程
刚体的运动分解随质心的平动+绕质心的转动 六个独立的方程 刚体有六个独立变量. 故质心运动及绕质心转动两组方程式 恰好确定刚体的运动情况,就是刚体运动的基本微分方程. 可用动能定理 作为一个辅助方程来代替方程中的 任意一个. 注意: 刚体内力所作元功之和为零, 故刚体动能的微分 等于刚体在运动过程中外力所作的元功之和

刚体平衡方程 3 F=0 若刚体处于平衡状态,其充要条件: a=0 如为共面力系,诸力均位于y平面内,则平衡方程简化为 F=0,F,=0,M.=0 空间力系等其他情况,也可根据上述条件,得出具体平衡条件。 超卓课程
3 刚体平衡方程 0 0 M F 如为共面力系, 诸力均位于xy平面内, 则平衡方程简化为 0, 0, 0 Fx Fy M z 若刚体处于平衡状态,其充要条件: 空间力系等其他情况,也可根据上述条件,得出具体平衡条件