
第12章 矩阵位移法 K<D 12-1 概述 12-2 局部坐标下的单元刚度矩阵 12-3 整体坐标下的单元刚度矩阵 12-4 连续梁的整体刚度矩阵 12-5 刚架的整体刚度矩阵 12-6 等效结点荷载 12-7 计算步骤和算例 12-8 忽略轴向变形时矩形刚架的整体分析 12-9 桁架及组合结构的整体分析
第12章 矩阵位移法 12-1 概述 12-2 局部坐标下的单元刚度矩阵 12-3 整体坐标下的单元刚度矩阵 12-4 连续梁的整体刚度矩阵 12-5 刚架的整体刚度矩阵 12-6 等效结点荷载 12-7 计算步骤和算例 12-8 忽略轴向变形时矩形刚架的整体分析 12-9 桁架及组合结构的整体分析

12-1概述 矩阵位移法的理论基础是传统的位移法,只 是它的表达形式采用矩阵代数,而这种数学算法 便于编制计算机程序,实现计算过程的程序化。 矩阵位移法又可以称为杆件结构的有限元 矩阵位移法的基本步骤是: (1)结构的离散化: (2)单元分析; (3)整体分析
12-1 概述 矩阵位移法的理论基础是传统的位移法,只 是它的表达形式采用矩阵代数,而这种数学算法 便于编制计算机程序,实现计算过程的程序化。 矩阵位移法又可以称为杆件结构的有限元 矩阵位移法的基本步骤是: (1)结构的离散化; (2)单元分析; (3)整体分析

12-1概述 任务 意义 建立杆端力与杆端位 单元 移间的刚度方程,形 用矩阵形式表示杆 分析 件的转角位移方程 成单元刚度矩阵 由变形条件和平衡条件 整体 建立结点力与结点位移 用矩阵形式表示位 分析 间的刚度方程,形成整 移法基本方程 体刚度矩阵
12-1 概述 任 务 意义 单元 分析 建立杆端力与杆端位 移间的刚度方程,形 成单元刚度矩阵 用矩阵形式表示杆 件的转角位移方程 任 务 意义 整体 分析 由变形条件和平衡条件 建立结点力与结点位移 间的刚度方程,形成整 体刚度矩阵 用矩阵形式表示位 移法基本方程
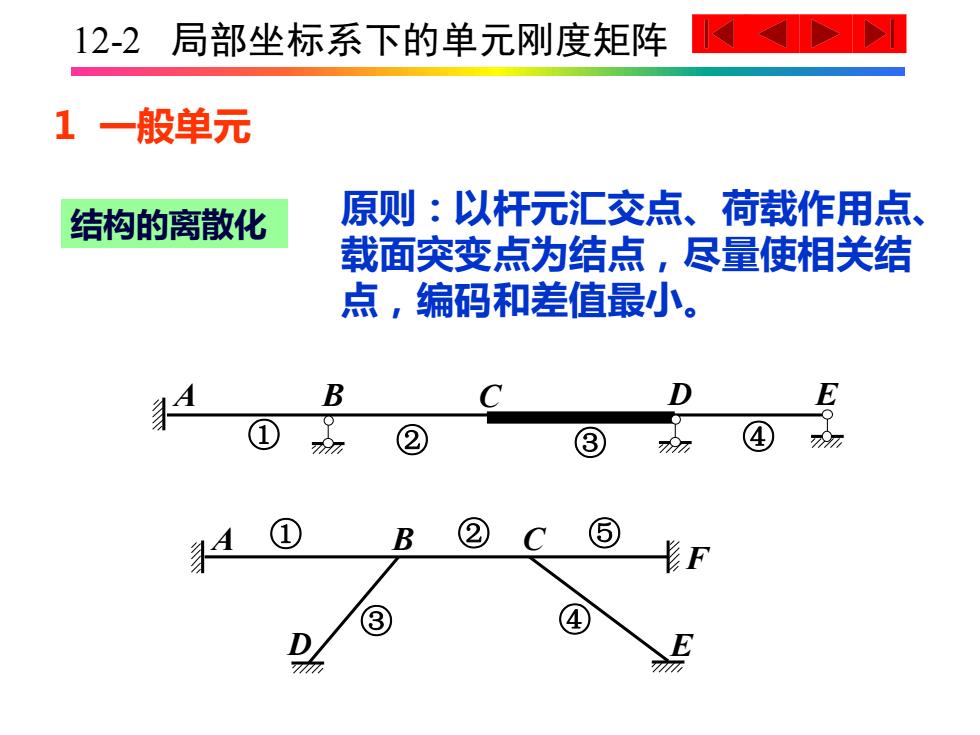
12-2局部坐标系下的单元刚度矩阵 1一般单元 结构的离散化 原侧:以杆元汇交点、荷载作用点、 载面突变点为结点,尽量使相关结 点,编码和差值最小。 B D E ① ② ③ ④ 9玩 ① B ⑤
12-2 局部坐标系下的单元刚度矩阵 1 一般单元 A B C D E ① ② ③ ④ F ⑤ A B D E ① ② ③ ④ C 结构的离散化 原则:以杆元汇交点、荷载作用点、 载面突变点为结点,尽量使相关结 点,编码和差值最小
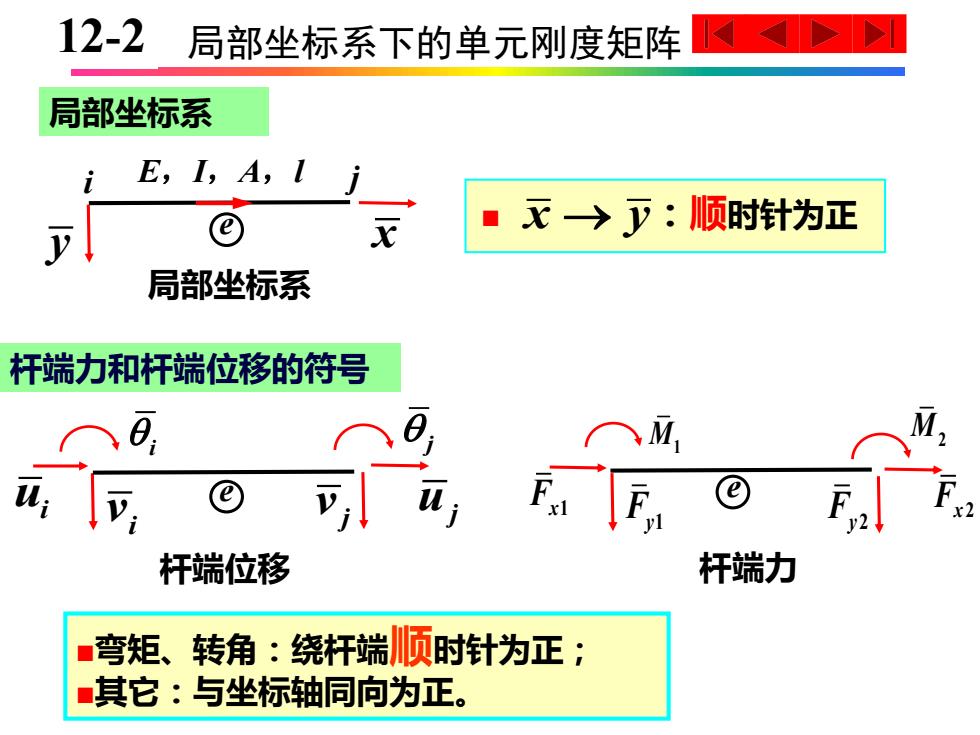
12-2 局部坐标系下的单元刚度矩阵 局部坐标系 E,I,A, 灭→少:顺时针为正 y 局部坐标系 杆端力和杆端位移的符号 ⌒M, ,E,© 杆端位移 杆端力 弯矩、转角:绕杆端顺时针为正; 其它:与坐标轴同向为正
10-2 局部坐标系下的单元刚度矩阵 杆端力和杆端位移的符号 ■弯矩、转角:绕杆端顺时针为正; ■其它:与坐标轴同向为正。 i E,I,A,l j y x ■ x y → :顺时针为正 i j ui i v j v uj e 杆端位移 F x1 F y1 F y2 F x 2 M1 M2 e 杆端力 局部坐标系 e 局部坐标系 12-2
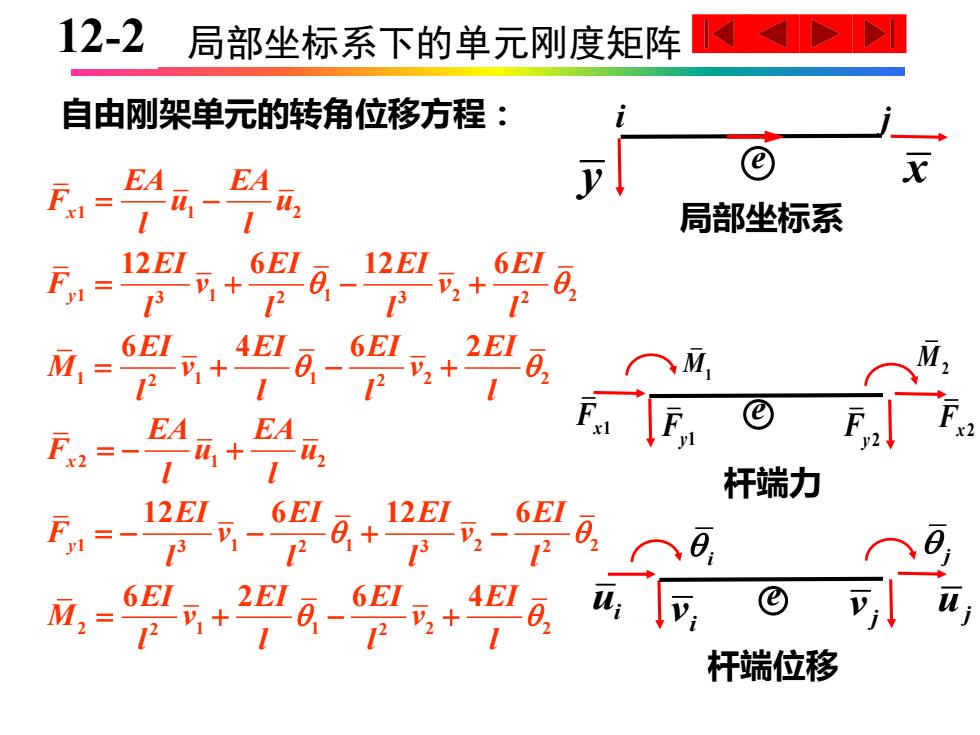
12-2 局部坐标系下的单元刚度矩阵 自由刚架单元的转角位移方程: EA_ EA 1 局部坐标系 12EI 6EI 12EI_6EI V+ 2 + 2 M= 6E1 4EI 6E-,2E1 可+ 0、 2 -V2+- M M, F EA EA y2 杆端力 12E1 6EI 12EI 日+ 6EI V- 3 12 6EI_2EI D ,© 12 + 2 + 杆端位移
10-2 局部坐标系下的单元刚度矩阵 1 1 2 1 1 1 2 2 3 2 3 2 1 1 1 2 2 2 2 2 1 2 1 1 1 2 2 3 2 3 2 2 1 1 2 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 x y x y EA EA F u u l l EI EI EI EI F v v l l l l EI EI EI EI M v v l l l l EA EA F u u l l EI EI EI EI F v v l l l l EI EI EI EI M v v l l l l = − = + − + = + − + = − + = − − + − = + − + 自由刚架单元的转角位移方程: F x1 F y1 F y2 F x 2 M1 M2 e 杆端力 i j ui i v j v uj e 杆端位移 i y x 局部坐标系 e j 12-2
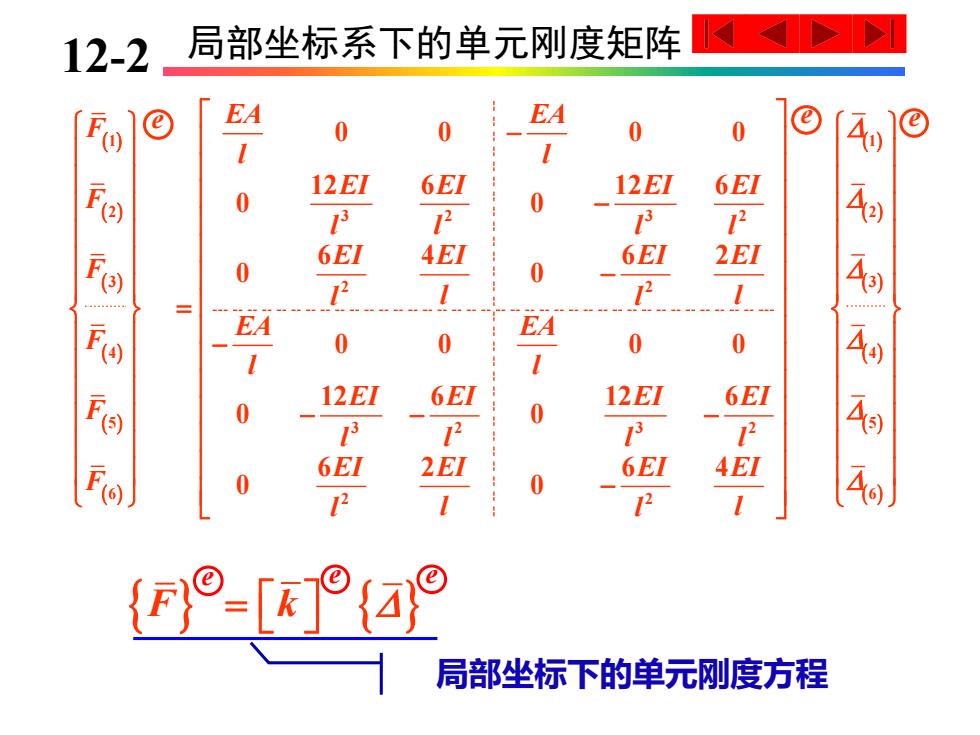
12-2 局部坐标系下的单元刚度矩阵 EA EA 0 0 0 F 12E7 6EI 12EI 6EI 0 0 12 6EI 4EI 6EI 2EI 0 0 4 12 EA EA 0 0 0 0 12EI 6EI 12EI 6E1 0 0 12 P 6EI 2EI 6EI 0 0 4 /2 2 F}© 局部坐标下的单元刚度方程
10-2 局部坐标系下的单元刚度矩阵 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 2 3 2 3 2 3 3 2 2 4 4 5 3 2 3 2 6 2 2 0 0 0 0 12 6 12 6 0 0 6 4 6 2 0 0 0 0 0 0 12 6 12 6 0 0 6 2 6 4 0 0 EA EA F l l EI EI EI EI F l l l l EI EI EI EI F l l l l EA EA F l l EI EI EI EI F l l l l EI EI EI EI F l l l l − − − = − − − − − ( ) ( ) 5 6 F k = 局部坐标下的单元刚度方程 e e e e e e 12-2
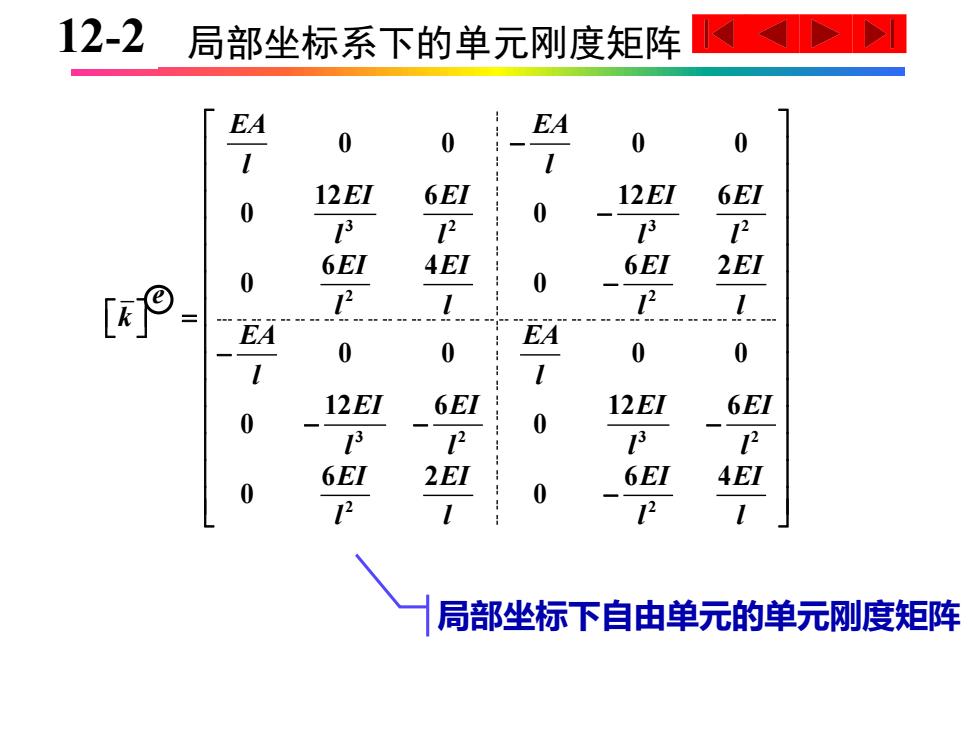
12-2 局部坐标系下的单元刚度矩阵 EA EA 0 12E1 6EI 12E1 6EI 0 0 13 6EI 4EI 6EI 2EI 0 [ 2 EA EA 0 0 0 12E1 6EI 12EI 6EI 0 3 2 12 6EI 2EI 6EI 4EI 0 0 12 12 局部坐标下自由单元的单元刚度矩阵
10-2 局部坐标系下的单元刚度矩阵 3 2 3 2 2 2 3 2 3 2 2 2 0 0 0 0 12 6 12 6 0 0 6 4 6 2 0 0 0 0 0 0 12 6 12 6 0 0 6 2 6 4 0 0 EA EA l l EI EI EI EI l l l l EI EI EI EI l l l l k EA EA l l EI EI EI EI l l l l EI EI EI EI l l l l − − − = − − − − − e 局部坐标下自由单元的单元刚度矩阵 12-2
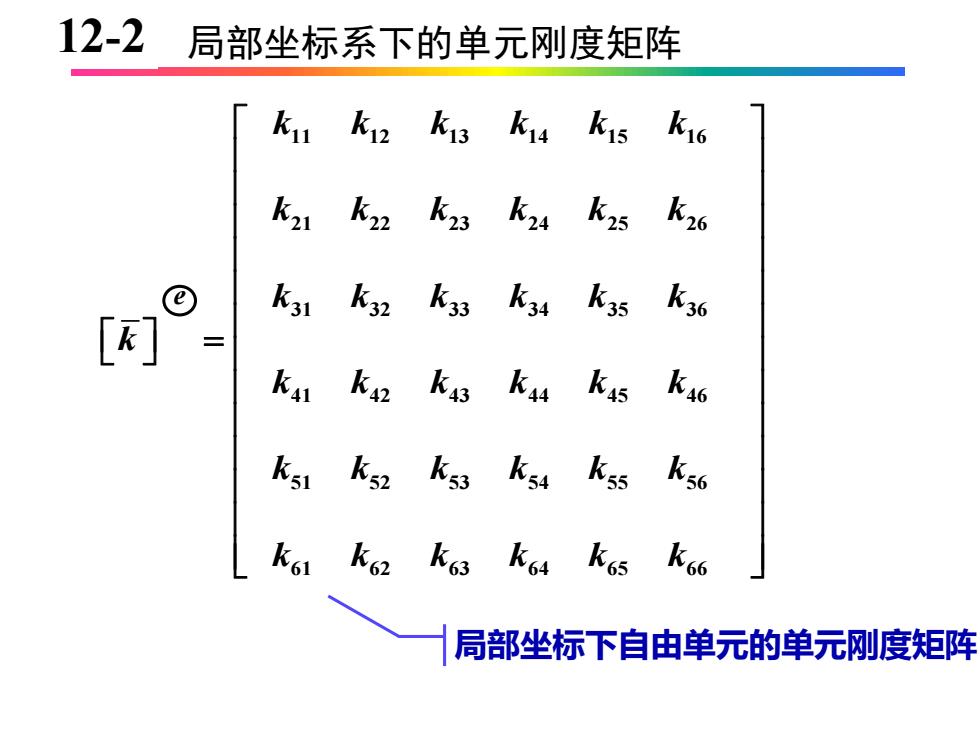
12-2 局部坐标系下的单元刚度矩阵 ku k k13k14k15k16 k2 k2 k23 k24k25 k26 k31 k32 k33 k4k35k36 [] Kat k42 k44 k45 k46 kst k52 k53 k54 kss k56 k61 k62 k66 局部坐标下自由单元的单元刚度矩阵
10-2 局部坐标系下的单元刚度矩阵 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66 k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k = e 局部坐标下自由单元的单元刚度矩阵 12-2
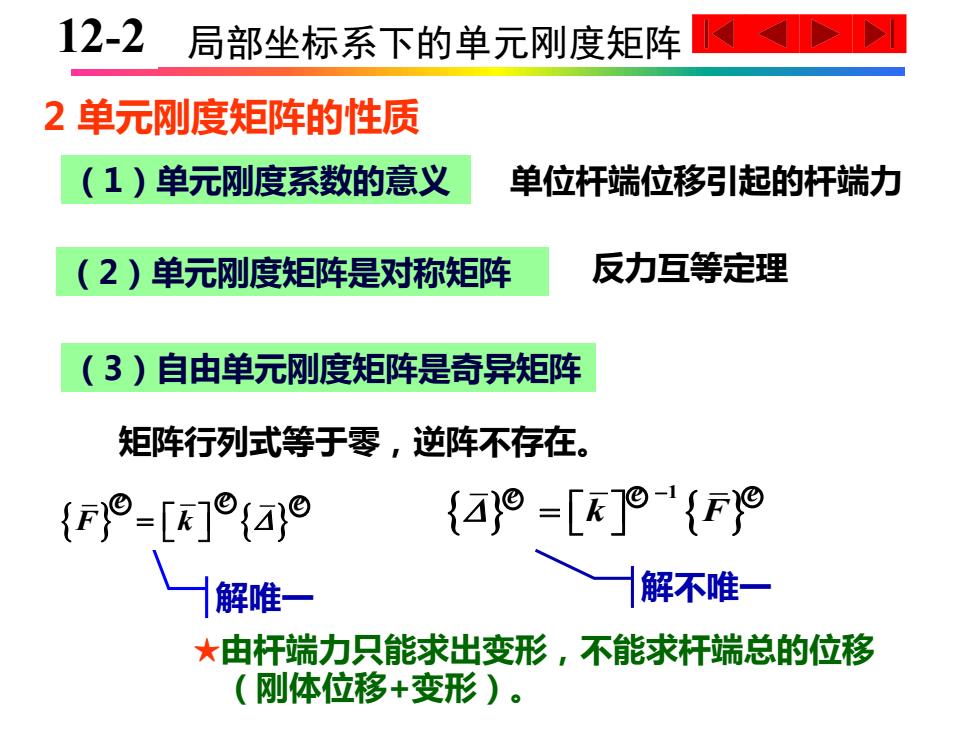
12-2 局部坐标系下的单元刚度矩阵 2单元刚度矩阵的性质 (1)单元刚度系数的意义 单位杆端位移引起的杆端力 (2)单元刚度矩阵是对称矩阵 反力互等定理 (3)自由单元刚度矩阵是奇异矩阵 矩阵行列式等于零,逆阵不存在。 {F=[]®{a}9 {a°-[k]-{F9 解唯一 解不唯一 ★由杆端力只能求出变形,不能求杆端总的位移 (刚体位移+变形)
10-2 局部坐标系下的单元刚度矩阵 2 单元刚度矩阵的性质 (1)单元刚度系数的意义 单位杆端位移引起的杆端力 (2)单元刚度矩阵是对称矩阵 反力互等定理 (3)自由单元刚度矩阵是奇异矩阵 矩阵行列式等于零,逆阵不存在。 解不唯一 ★由杆端力只能求出变形,不能求杆端总的位移 (刚体位移+变形)。 解唯一 F k = 1 k F − = e e e e e e 12-2