
第十一章影响线及其应用 一、基本概念 本章将讨论在移动荷载作用下结构的反力和内力计算向愿,影响线是解决此类问题的工 只和手段。 影响线定义:当一个方向不变的单位荷载在结构上移动时,表示某一量值变化规律的函 数图形,成为该量值的图形。 会制影响线有两种基本方法:静力法和机动法。静力法是基础,它适合各种结构,机动 法快捷方便,它适宜于梁式结构。 求最不利的荷载位置及最大的量值:当所求量值是直角三角形时,不需要判别式,原则 上将数值大且密集的荷载摆放在影响线竖标大的区域即可:当所求量值是任意三角形或多边 形时,需要用判别式判别摆放的荷载位置是否是最不利的位置,再求最大量值。 二、部分题解 11-7试用静力法作图示结构中M。、FD、Fc影响线 2n E 解: M,= (0≤x≤2) M=2- (2≤x≤6) FoD- (0≤x<2) FoD =1-* (2<x≤6) 4 x=高x0sx≤6) MD响线 ) 0.5 05 Q56n影响线 FNBC影响线 25
第十一章 影响线及其应用 一、基本概念 本章将讨论在移动荷载作用下结构的反力和内力计算问题,影响线是解决此类问题的工 具和手段。 影响线定义:当一个方向不变的单位荷载在结构上移动时,表示某一量值变化规律的函 数图形,成为该量值的图形。 绘制影响线有两种基本方法:静力法和机动法。静力法是基础,它适合各种结构,机动 法快捷方便,它适宜于梁式结构。 求最不利的荷载位置及最大的量值:当所求量值是直角三角形时,不需要判别式,原则 上将数值大且密集的荷载摆放在影响线竖标大的区域即可;当所求量值是任意三角形或多边 形时,需要用判别式判别摆放的荷载位置是否是最不利的位置,再求最大量值。 二、部分题解 11-7 试用静力法作图示结构中 MD 、 FQD 、 FNBC 影响线 解: 2 D x M = (0 2) x 2 2 D x M = − (2 6) x 4 QD x F = − (0 2) x 1 4 QD x F = − (2 6) x 5 12 F x NBC = ( 0 6 x )
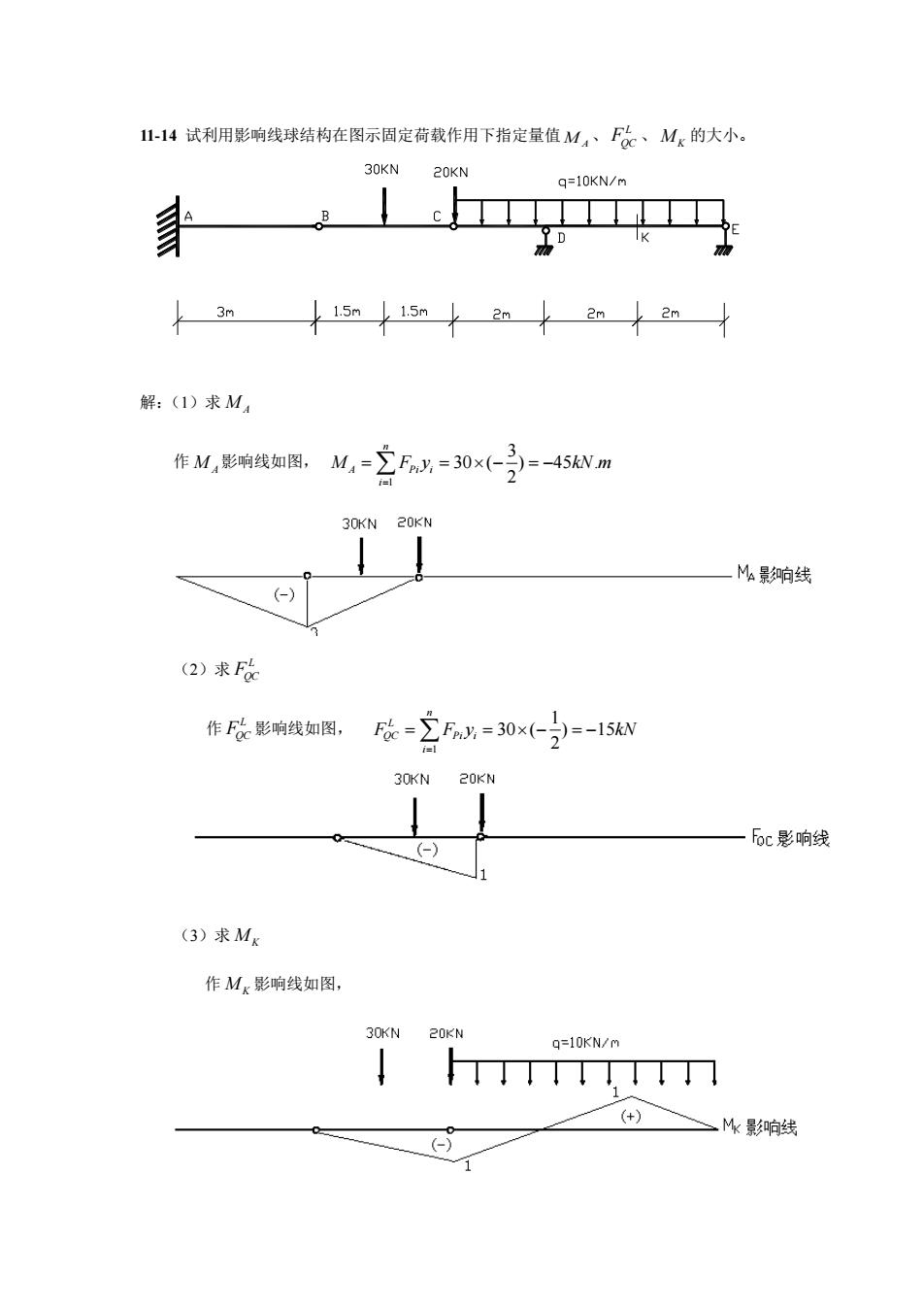
-14试利用影响线球结构在图示周定荷载作用下指定量值M,、F张、Mx的大小。 30KN 20KN q=10KN/m L k3n大15m15n2m大2m 解:(1)求M 30KN 20KN M响线 (2)求F 作F必影响线如图, F依=2Fny=30x(-=-15N 30KN 20KN -6c影响线 (3)求Mx 作M影响线如图 30KN 20KN q=10KN/m 影响线
11-14 试利用影响线球结构在图示固定荷载作用下指定量值 M A 、 L FQC 、 MK 的大小。 解:(1)求 M A 作 M A 影响线如图, 1 3 30 ( ) 45 . 2 n A Pi i i M F y kN m = = = − = − (2)求 L FQC 作 L FQC 影响线如图, 1 1 30 ( ) 15 2 n L QC Pi i i F F y kN = = = − = − (3)求 MK 作 MK 影响线如图
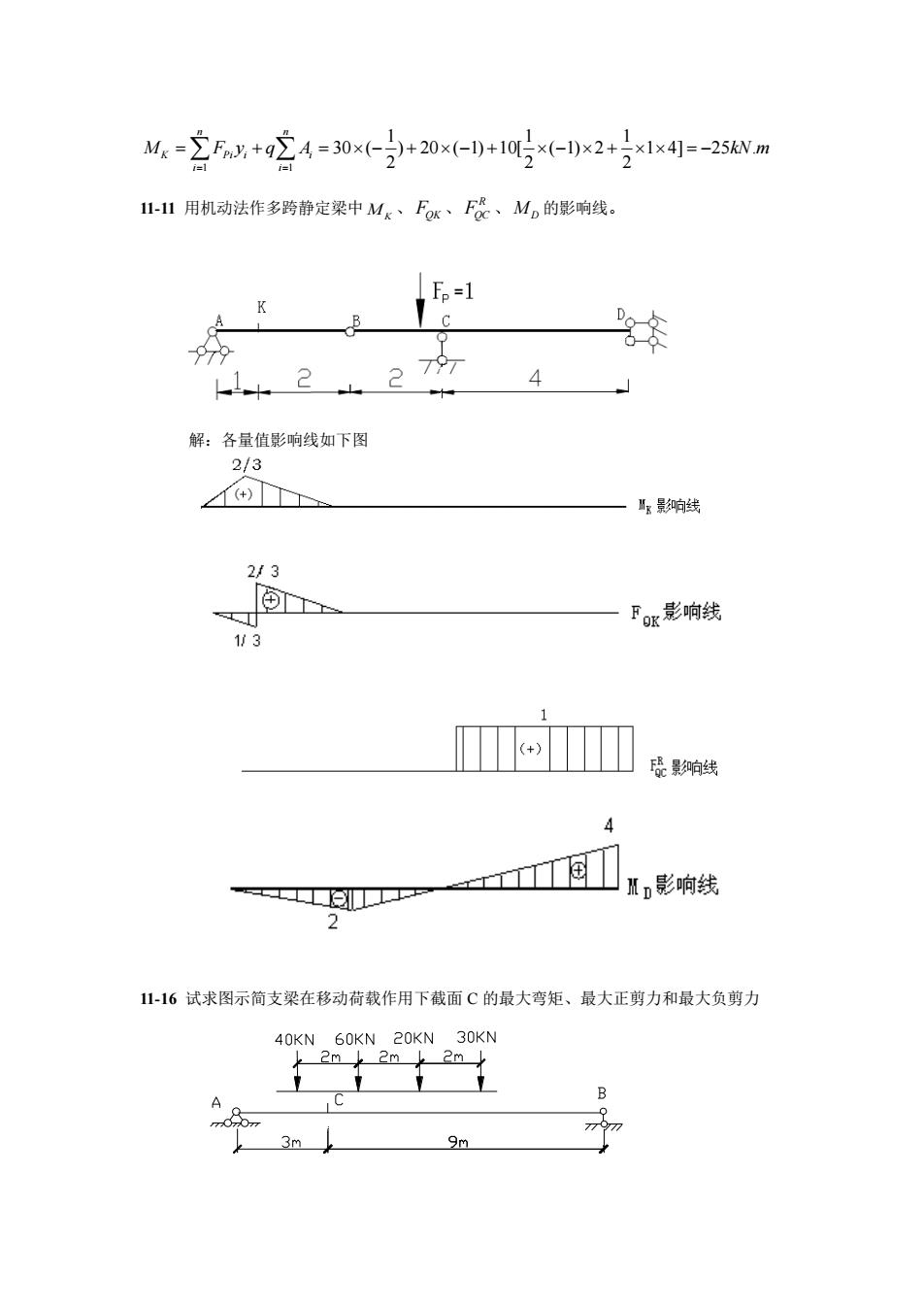
M:-2x+24=30x(-3+20x-+10写-g2+x1x4=-25vVm 1I-II用机动法作多跨静定梁中Mk、Fox、F、Mo的影响线。 A B 12 山27 4 解:各量值影响线如下图 2/3 ,影响线 2/3 FK影响线 o生 4 工工于 图口,影响线 1-16试求图示简支梁在移动荷载作用下截面C的最大弯矩、最大正剪力和最大负剪力 30KN A 9m
1 1 1 1 1 30 ( ) 20 ( 1) 10[ ( 1) 2 1 4] 25 . 2 2 2 n n K Pi i i i i M F y q A kN m = = = + = − + − + − + = − 11-11 用机动法作多跨静定梁中 MK 、 FQK 、 R FQC 、 MD 的影响线。 解:各量值影响线如下图 11-16 试求图示简支梁在移动荷载作用下截面 C 的最大弯矩、最大正剪力和最大负剪力 试求图示简支梁在移动荷载作用下截面 的最大弯矩,最 大正剪力和最大负剪力
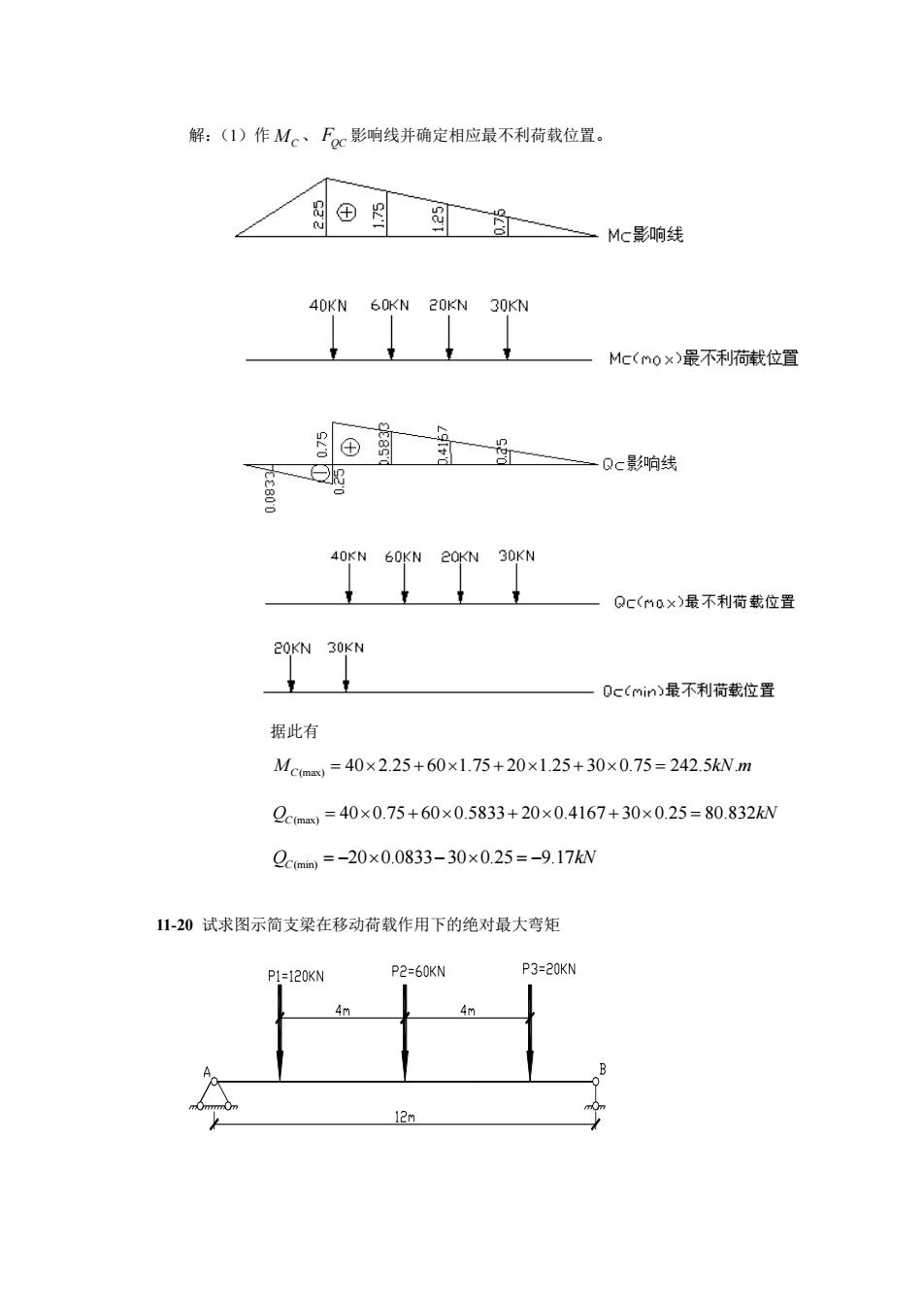
解:(I)作Mc、Fc影响线并确定相应最不利荷载位置。 周田图图的—Mk影响线 Mc(MOx)最不利荷截位置 ④的的 Qc影响线 T网 Qc(m0x)最不利荷载位置 Y 0c(mim)最不利荷载位置 据此有 Mcmm=40×2.25+60×1.75+20×1.25+30×0.75=242.5kWm Q=40×0.75+60×0.5833+20×0.4167+30×0.25=80.832kW Qmm=-20×0.0833-30×0.25=-9.17kW 11-20试求图示简支梁在移动荷载作用下的绝对最大弯矩 2=60K P3=20K 20K 4
解:(1)作 MC 、 FQC 影响线并确定相应最不利荷载位置。 据此有 (max) 40 2.25 60 1.75 20 1.25 30 0.75 242.5 . M kN m C = + + + = (max) 40 0.75 60 0.5833 20 0.4167 30 0.25 80.832 Q kN C = + + + = (min) 20 0.0833 30 0.25 9.17 Q kN C = − − = − 11-20 试求图示简支梁在移动荷载作用下的绝对最大弯矩
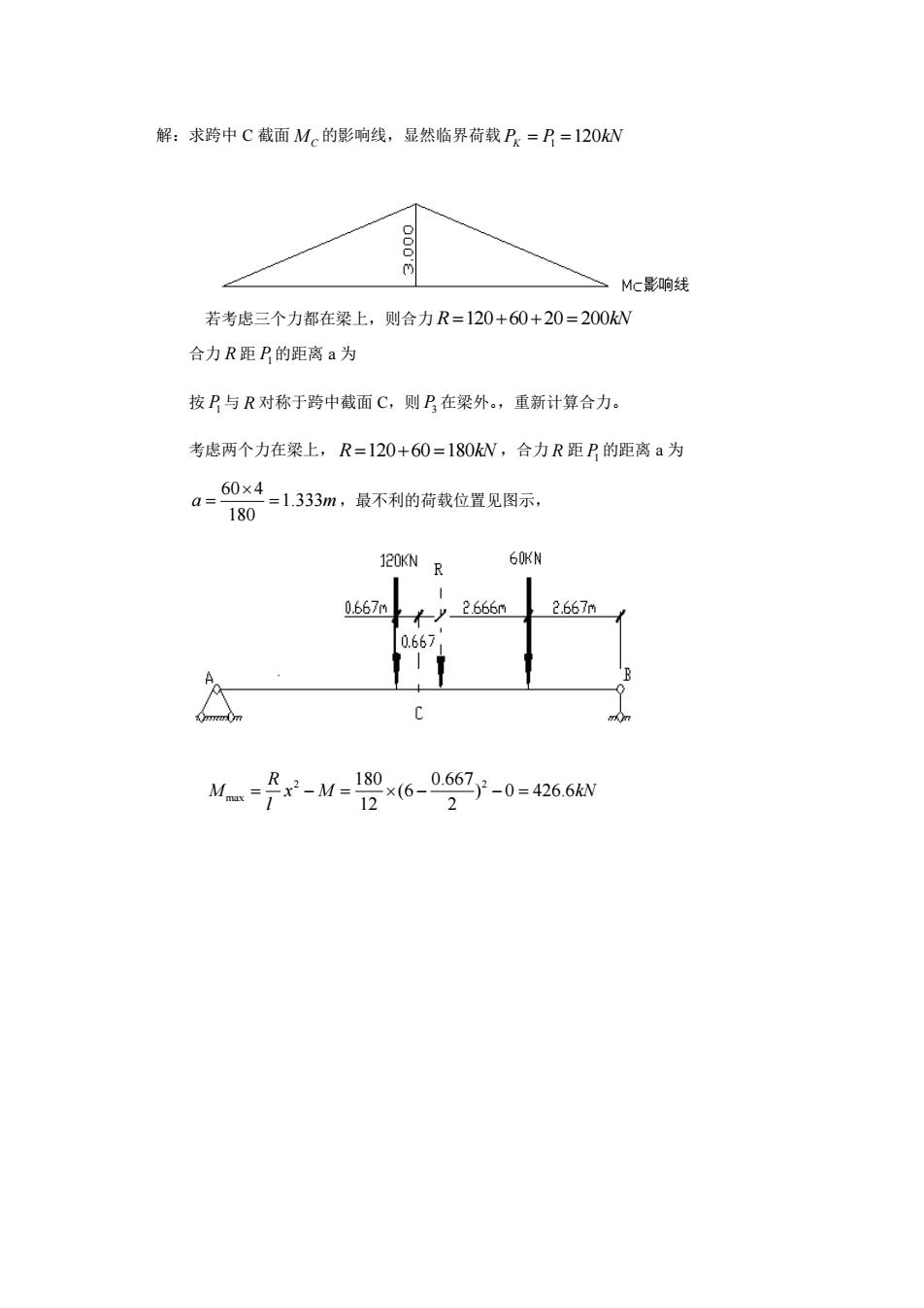
解:求跨中C截面M的影响线,显然临界荷载P=B=120kW Mc影响线 若考虑三个力都在梁上,则合力R=120+60+20=200kW 合力R距P的距离a为 按乃与R对称于跨中截面C,则E在梁外。,重新计算合力。 考虑两个力在梁上,R=120+60=180kW,合力R距P的距离a为 a=60x4-13m,最不利的荷我位置见图示, 180 120KN R 60KN 9667 Mn=2-M=180x16-06}-0=4266kN
解:求跨中 C 截面 MC 的影响线,显然临界荷载 1 120 P P kN K = = 若考虑三个力都在梁上,则合力 R kN = + + = 120 60 20 200 合力 R 距 P1 的距离 a 为 按 P1 与 R 对称于跨中截面 C,则 P3 在梁外。,重新计算合力。 考虑两个力在梁上, R kN = + = 120 60 180 ,合力 R 距 P1 的距离 a 为 60 4 1.333 180 a m = = ,最不利的荷载位置见图示, 2 2 max 180 0.667 (6 ) 0 426.6 12 2 R M x M kN l = − = − − =